
导航 均值是随机变量可能取值关于取值概率的加权平均数,它综 合了随机变量的取值和取值的概率,反映了随机变量取值的
导航 均值是随机变量可能取值关于取值概率的加权平均数,它综 合了随机变量的取值和取值的概率,反映了随机变量取值的 平均水平

微训练1若随机变量X的分布列为 导航 1 0 1 1-2 1-6 1-3 则EX)=( A.0 B.-1 c D 1-2 答案:C 解析:B0含p=I)0×+1×后 =1
微训练 导航 1若随机变量X的分布列为 X -1 0 1 P 𝟏 𝟐 𝟏 𝟔 𝟏 𝟑 则E(X)=( ) A.0 B.-1 C.- 𝟏 𝟔 D.- 𝟏 𝟐 答案:C 解析:E(X)= ∑ 𝒊=𝟏 𝒏 xipi=(-1)× 𝟏 𝟐 +0× 𝟏 𝟔 +1× 𝟏 𝟑 =- 𝟏 𝟔

导 2.两点分布 般地,如果随机变量X服从两点分布,那么E)=0X(1-p) +1Xp=卫. 3.均值的性质 一般地,该结论成立:E(X+b)= 微训练2设E)=10,侧E3X+5)= 答案:35 解析:E3X+5)=3EX)+5=3X10+5=35
导航 2.两点分布 一般地,如果随机变量X服从两点分布,那么E(X)=0×(1-p) +1×p=p. 3.均值的性质 一般地,该结论成立:E(aX+b)= aE(X)+b . 微训练2设E(X)=10,则E(3X+5)= . 答案:35 解析:E(3X+5)=3E(X)+5=3×10+5=35
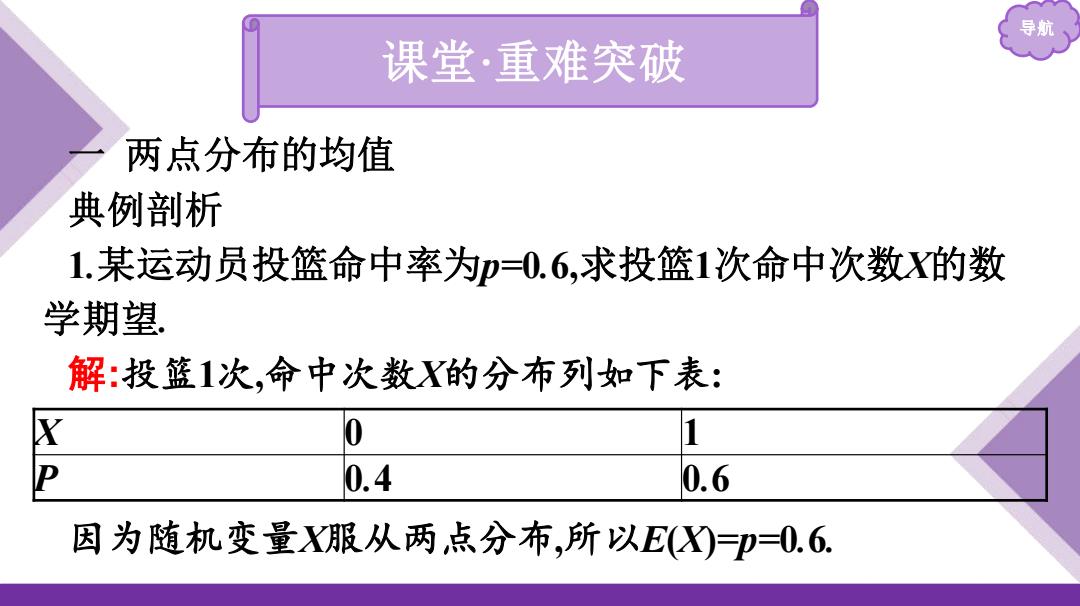
导航 课堂·重难突破 两点分布的均值 典例剖析 1.某运动员投篮命中率为p=0.6,求投篮1次命中次数X的数 学期望 解:投篮1次,命中次数X的分布列如下表: 0 1 0.4 0.6 因为随机变量X服从两点分布,所以EX)=卫=0.6
导航 一 两点分布的均值 典例剖析 1.某运动员投篮命中率为p=0.6,求投篮1次命中次数X的数 学期望. 解:投篮1次,命中次数X的分布列如下表: 因为随机变量X服从两点分布,所以E(X)=p=0.6. 课堂·重难突破 X 0 1 P 0.4 0.6
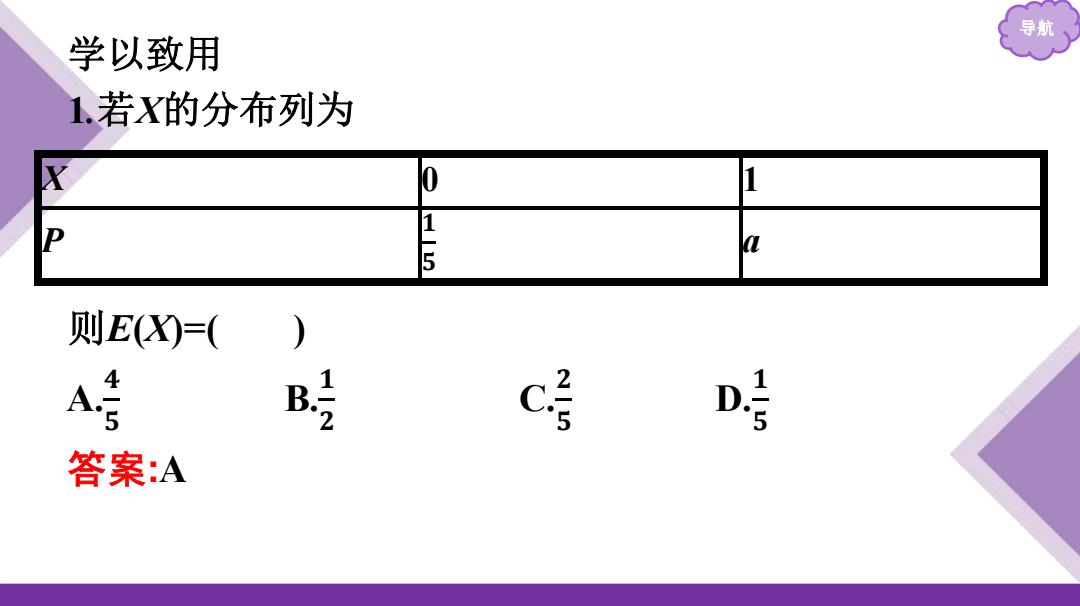
导航 学以致用 1若X的分布列为 0 1 1-5 则EX)=( B时 c 答案:A
导航 学以致用 1.若X的分布列为 则E(X)=( ) X 0 1 P 𝟏𝟓 a A.𝟒𝟓 B.𝟏𝟐 C.𝟐𝟓 D.𝟏𝟓 答案 :A