
el 2 es 常用术语: e (1)端点相同的边称为环 (2)若一对顶点之间有两条以上的边联结,则这些边称为重边, (3)有边联结的两个顶点称为相邻的顶点,有一个公共端点的边 称为相邻的边. (4)边和它的端点称为互相关联的。 (5)既没有环也没有平行边的图,称为简单图 (6)任意两顶点都相邻的简单图,称为完备图,记为K,其中n 为顶点的数目. (7)若=XUY,X⌒Y=Φ,且X中任两顶点不相邻,Y中任两顶 点不相邻,则称G为二元图:若X中每一顶点皆与Y中一切顶点 相邻,则G称为完备二元图,记为Kmn,其中m,n分别为X与Y的项 点数目
常用术语: (1)端点相同的边称为环. (2)若一对顶点之间有两条以上的边联结,则这些边称为重边. (3)有边联结的两个顶点称为相邻的顶点,有一个公共端点的边 称为相邻的边. (4)边和它的端点称为互相关联的. (5)既没有环也没有平行边的图,称为简单图. (6)任意两顶点都相邻的简单图,称为完备图,记为 Kn,其中 n 为顶点的数目. ( 7)若 V=X Y,X Y= ,且 X 中任两顶点不相邻,Y 中任两顶 点不相邻,则称 G 为二元图;若 X 中每一顶点皆与 Y 中一切顶点 相邻,则 G 称为完备二元图,记为 Km,n,其中 m,n 分别为 X 与 Y 的顶 点数目.
返回
返回
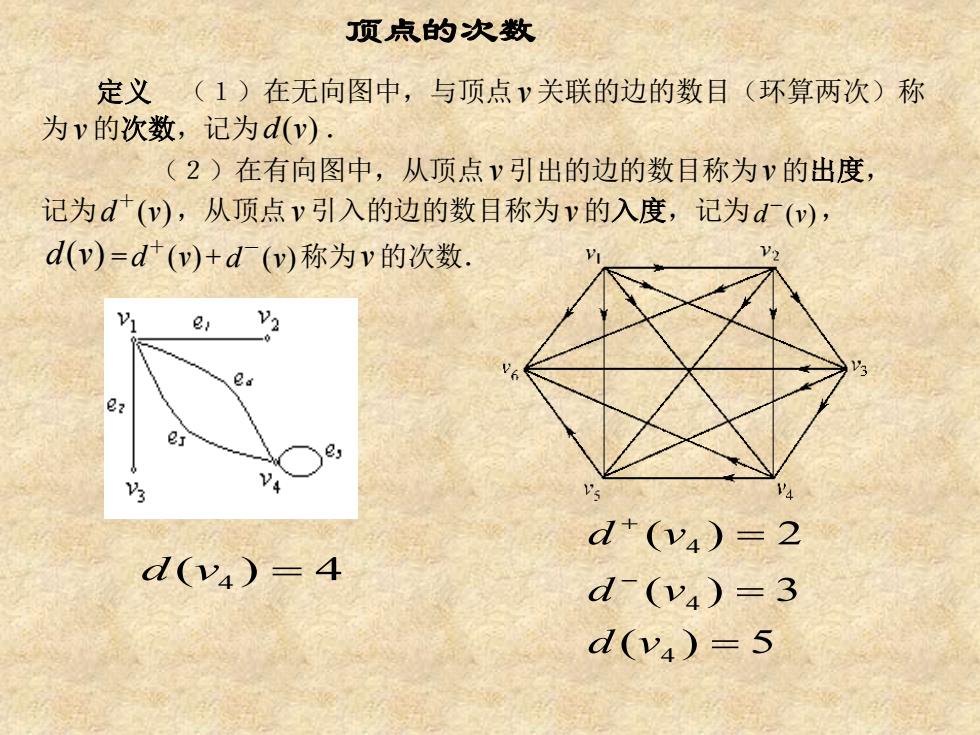
顶点的次数 定义(1)在无向图中,与顶点v关联的边的数目(环算两次)称 为v的次数,记为d(v). (2)在有向图中,从顶点v引出的边的数目称为v的出度, 记为d(y),从顶点v引入的边的数目称为v的入度,记为d(w), d(v)=d(v)+d厂(v)称为v的次数 e, V2 ez d+(y4)=2 d(y4)=4 d(y4)=3 d(v4)=5
顶点的次数 定义 (1)在无向图中,与顶点 v 关联的边的数目(环算两次)称 为v 的次数,记为d v( ) . (2)在有向图中,从顶点v 引出的边的数目称为v 的出度, 记为d v( ) + ,从顶点v 引入的边的数目称为v 的入度,记为d v( ) - , d v( ) = d v( ) + + d v( ) - 称为 v 的次数. 4 d v( ) 4 = ( ) 5 ( ) 3 ( ) 2 4 4 4 = = = − + d v d v d v

定理1 ∑d()=28(G) vel/(G) 推论1任何图中奇次顶点的总数必为偶数. 例在一次聚会中,认识奇数个人的人数一定是偶数 返回
定理1 ( ) 2 ( ) ( ) d v G v V G = 推论1 任何图中奇次顶点的总数必为偶数. 例 在一次聚会中,认识奇数个人的人数一定是偶数. 返回
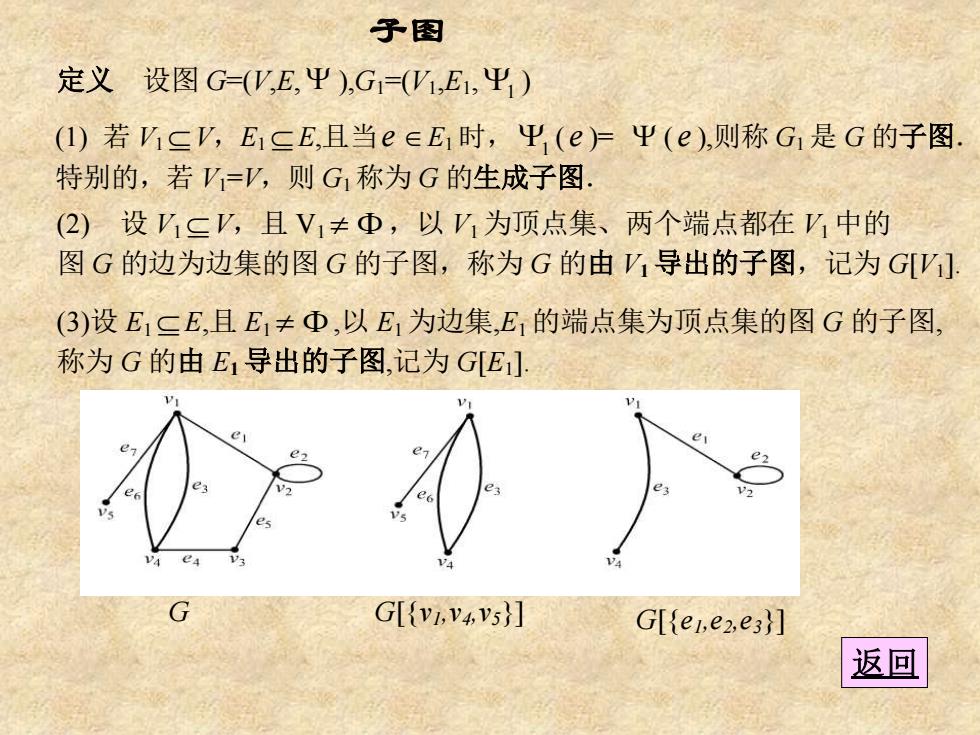
子图 定义设图G=(V,E,平),G1=(W,E1,平1) (1)若1sV,EsE,且当e∈E时,Y(e)=Ψ(e),则称G1是G的子图. 特别的,若V=V,则G称为G的生成子图. (2)设V三,且V1≠Φ,以V1为顶点集、两个端点都在中的 图G的边为边集的图G的子图,称为G的由导出的子图,记为GV] (3)设E1三E,且E1≠①,以E1为边集,E1的端点集为顶点集的图G的子图, 称为G的由E导出的子图,记为GE] G[{v,v4v5}] GHeLe2e3)] 返回
子图 定义 设图 G=(V,E, ),G1 =(V1,E1,1 ) (1) 若 V1 V,E1 E,且当e E1 时,1 ( e )= ( e ),则称 G1是 G 的子图. 特别的,若 V1 =V,则 G1称为 G 的生成子图. (2) 设 V1 V,且 V1 ,以 V1为顶点集、两个端点都在 V1中的 图 G 的边为边集的图 G 的子图,称为 G 的由 V1导出的子图,记为 G[V1 ]. (3)设 E1 E,且 E1 ,以 E1为边集,E1的端点集为顶点集的图 G 的子图, 称为 G 的由 E1导出的子图,记为 G[E1 ]. G G[{v1,v4,v5 }] G[{e1,e2,e3 }] 返回