
历安毛子代枚大兽 第二讲:基本概念与结构模型 XIDIAN UNIVERSITY >基本概念 (1)网络的图表示 (2)节点的聚类系数 (3)节点的介数 (4) 平均度和度分布 >结构模型 (1)小世界网络 (2)无标度网络 (3)社区网络 2
基本概念 (1)网络的图表示 (2)节点的聚类系数 (3)节点的介数 (4)平均度和度分布 结构模型 (1)小世界网络 (2)无标度网络 (3)社区网络 第二讲:基本概念与结构模型 2
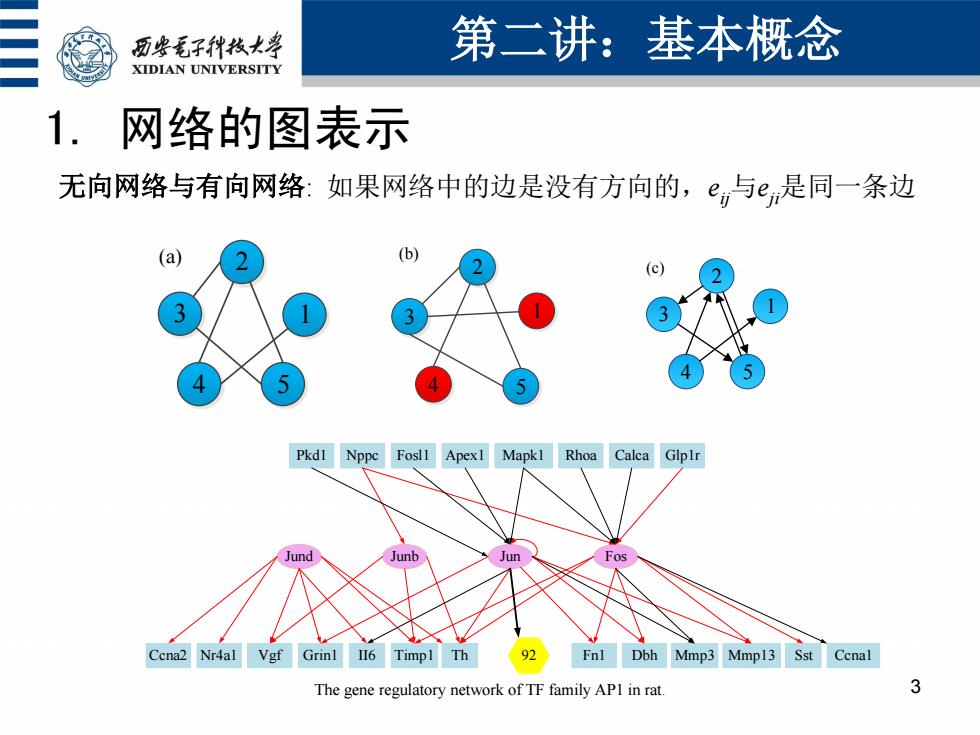
历些毛子代枝大学 第二讲:基本概念 XIDIAN UNIVERSITY 1. 网络的图表示 无向网络与有向网络:如果网络中的边是没有方向的,e,与e是同一条边 (a) (b Pkdl Nppc Fosll Apexl Mapkl Rhoa Calca Glplr Jund Junb iun Ccna2 Nr4al Vgf Grinl I6 Timpl Th Fnl Dbh Mmp3 Mmp13 Sst Ccnal The gene regulatory network of TF family APl in rat
1. 网络的图表示 第二讲:基本概念 3 3 1 2 4 5 (b) 3 1 2 4 5 (a) Ccna2 Nr4a1 Vgf Grin1 II6 Timp1 Th Fn1 Dbh Mmp3 Mmp13 Sst Ccna1 Pkd1 Nppc Fosl1 Apex1 Mapk1 Rhoa Calca Glp1r 92 Jund Junb Jun Fos The gene regulatory network of TF family AP1 in rat. 3 1 2 4 5 (c) 无向网络与有向网络: 如果网络中的边是没有方向的,eij与eji是同一条边
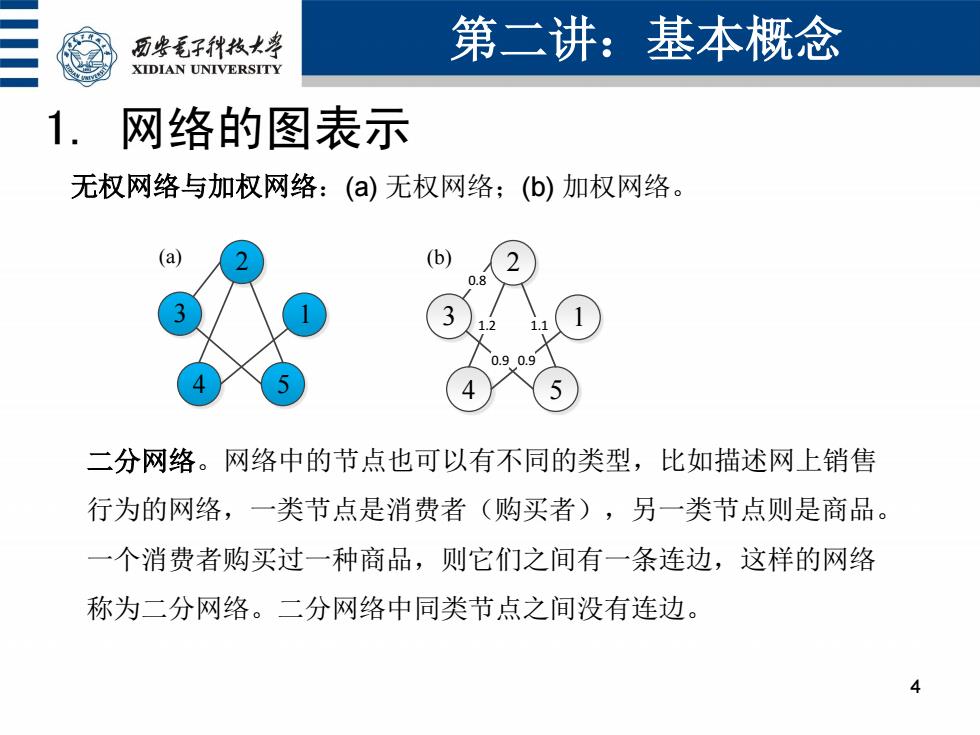
面些毛子种枚大票 第二讲:基本概念 XIDIAN UNIVERSITY 1. 网络的图表示 无权网络与加权网络:()无权网络;(b)加权网络。 a b 二分网络。网络中的节点也可以有不同的类型,比如描述网上销售 行为的网络,一类节点是消费者(购买者),另一类节点则是商品。 一个消费者购买过一种商品,则它们之间有一条连边,这样的网络 称为二分网络。二分网络中同类节点之间没有连边
1. 网络的图表示 第二讲:基本概念 4 3 1 2 4 5 (a) 无权网络与加权网络:(a) 无权网络;(b) 加权网络。 3 1 2 4 5 0.8 1.2 1.1 0.9 0.9 (b) 二分网络。网络中的节点也可以有不同的类型,比如描述网上销售 行为的网络,一类节点是消费者(购买者),另一类节点则是商品。 一个消费者购买过一种商品,则它们之间有一条连边,这样的网络 称为二分网络。二分网络中同类节点之间没有连边
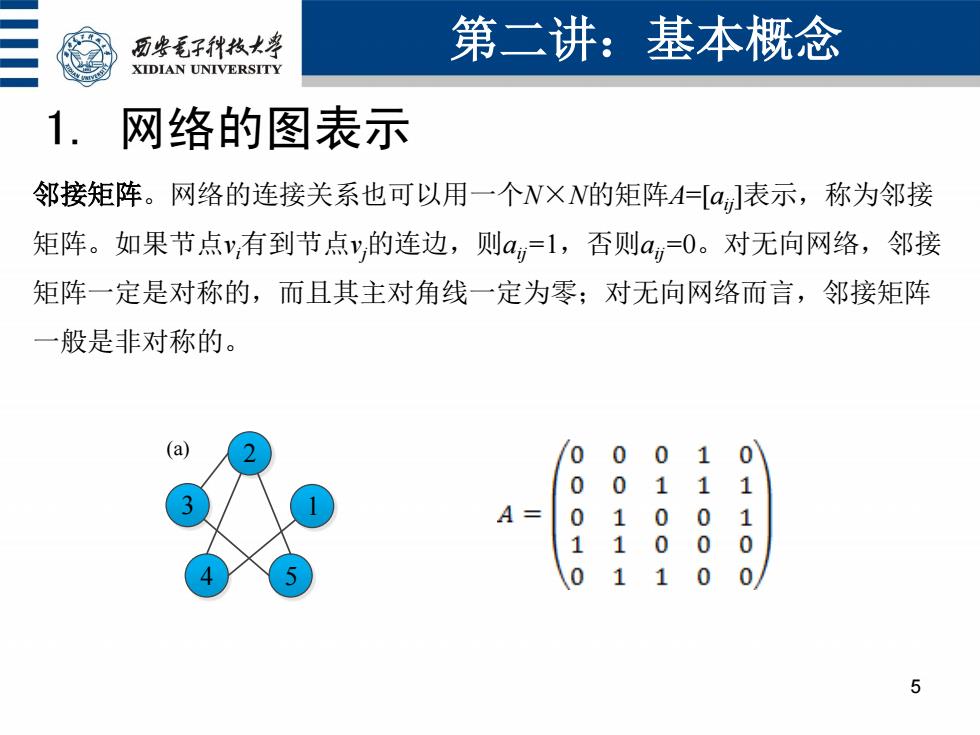
历些毛子代枝大学 第二讲:基本概念 XIDIAN UNIVERSITY 1. 网络的图表示 邻接矩阵。网络的连接关系也可以用一个N×N的矩阵A=[a,]表示,称为邻接 矩阵。如果节点y,有到节点y,的连边,则a=1,否则a,=0。对无向网络,邻接 矩阵一定是对称的,而且其主对角线一定为零;对无向网络而言,邻接矩阵 一般是非对称的。 (a) 00 0 0 1 01 A= 0 1 1 00 100 1 1 0 100 5
1. 网络的图表示 第二讲:基本概念 5 3 1 2 4 5 (a) 邻接矩阵。网络的连接关系也可以用一个N×N的矩阵A=[aij]表示,称为邻接 矩阵。如果节点vi有到节点vj的连边,则aij=1,否则aij=0。对无向网络,邻接 矩阵一定是对称的,而且其主对角线一定为零;对无向网络而言,邻接矩阵 一般是非对称的
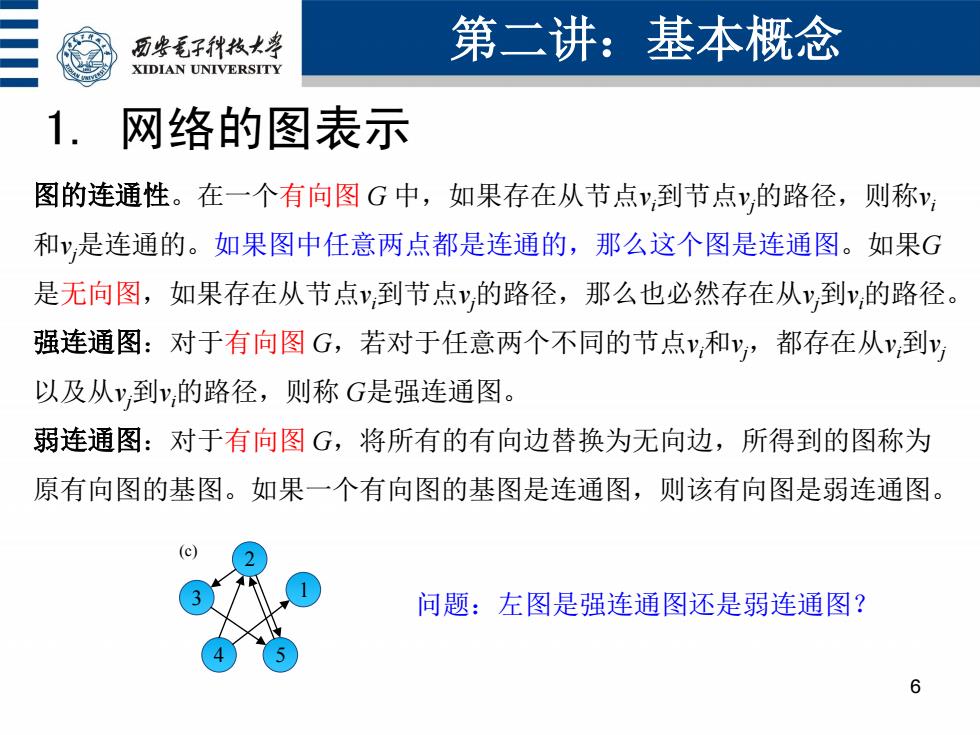
面些毛子种枚大票 第二讲:基本概念 XIDIAN UNIVERSITY 1. 网络的图表示 图的连通性。在一个有向图G中,如果存在从节点y,到节点y,的路径,则称y 和y是连通的。如果图中任意两点都是连通的,那么这个图是连通图。如果G 是无向图,如果存在从节点v,到节点y的路径,那么也必然存在从y,到y,的路径。 强连通图:对于有向图G,若对于任意两个不同的节点y,和y,都存在从v到y 以及从v,到y,的路径,则称G是强连通图。 弱连通图:对于有向图G,将所有的有向边替换为无向边,所得到的图称为 原有向图的基图。如果一个有向图的基图是连通图,则该有向图是弱连通图。 (c) 问题:左图是强连通图还是弱连通图? 6
1. 网络的图表示 第二讲:基本概念 6 图的连通性。在一个有向图 G 中,如果存在从节点vi到节点vj的路径,则称vi 和vj是连通的。如果图中任意两点都是连通的,那么这个图是连通图。如果G 是无向图,如果存在从节点vi到节点vj的路径,那么也必然存在从vj到vi的路径。 强连通图:对于有向图 G,若对于任意两个不同的节点vi和vj,都存在从vi到vj 以及从vj到vi的路径,则称 G是强连通图。 弱连通图:对于有向图 G,将所有的有向边替换为无向边,所得到的图称为 原有向图的基图。如果一个有向图的基图是连通图,则该有向图是弱连通图。 3 1 2 4 5 (c) 问题:左图是强连通图还是弱连通图?