
历华毛子种枝大学 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY (1)随机网络模型 (2)小世界网络 (3)无标度网络 (4)社区网络 2
(1)随机网络模型 (2)小世界网络 (3)无标度网络 (4)社区网络 第三讲:复杂网络结构模型 2
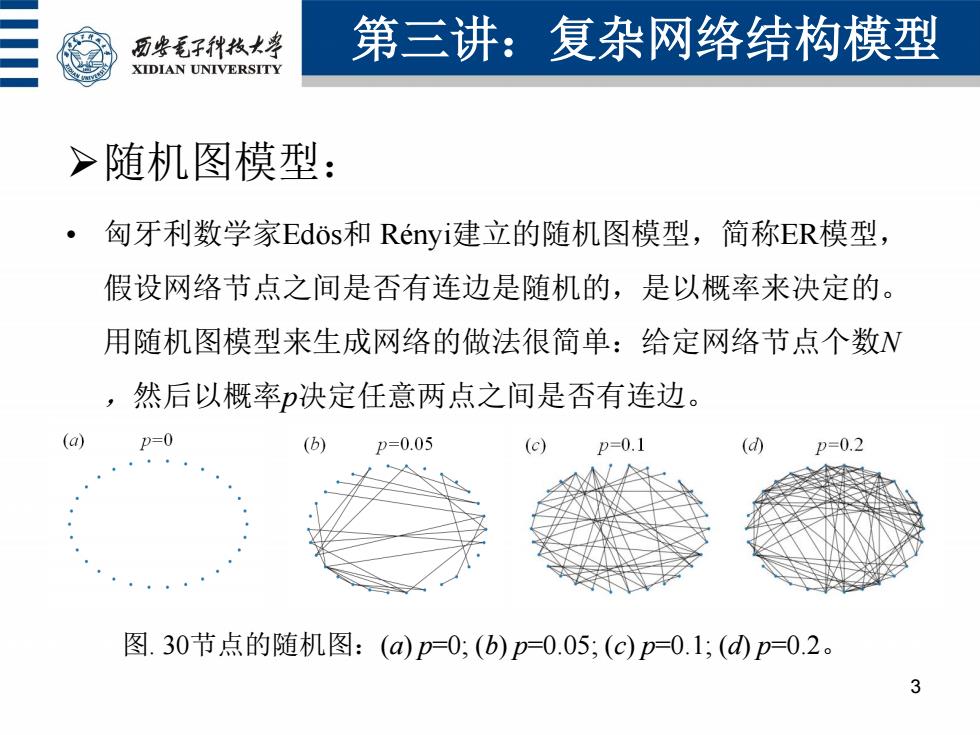
历些毛子代枝大学 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY >随机图模型: 匈牙利数学家Edos和Renyis建立的随机图模型,简称ER模型, 假设网络节点之间是否有连边是随机的,是以概率来决定的。 用随机图模型来生成网络的做法很简单:给定网络节点个数W ,然后以概率决定任意两点之间是否有连边。 (a) (b) p=0.05 (c) p=0.1 (d) p=0.2 图.30节点的随机图:(a)p=0,(b)p=0.05,(c)p-0.1;(d)p=0.2。 3
第三讲:复杂网络结构模型 3 随机图模型: • 匈牙利数学家Edös和 Rényi建立的随机图模型,简称ER模型, 假设网络节点之间是否有连边是随机的,是以概率来决定的。 用随机图模型来生成网络的做法很简单:给定网络节点个数N ,然后以概率p决定任意两点之间是否有连边。 图. 30节点的随机图:(a) p=0; (b) p=0.05; (c) p=0.1; (d) p=0.2

历安毛子代枚大等 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY >随机图模型的结构特征: 平均度<>:<>=pN-1)pW 网络密度:ER随机图中边的总数为M=Wp(N-1)/2,可能的最多边数为 N(N-1)/2,因此,网络密度为D=p。 聚集系数CC:在ER随机图模型中,任意两个节点相连的概率都是p, 也就是说CC=p。而在大规模网络中p远远小于1,也就是说ER随机图 不具有聚集特性。 (a) p=0 (b) p=0.05 (c) p=0.1 (d) p=0.2 图.30节点的随机图:(a)p=0,(b)p-0.05;(c)p-0.1;(d)p=0.2
第三讲:复杂网络结构模型 4 随机图模型的结构特征: • 平均度<k>:<k>=p(N-1)≈pN • 网络密度:ER随机图中边的总数为M=Np(N-1)/2, 可能的最多边数为 N(N-1)/2,因此,网络密度为D=p。 • 聚集系数CC:在ER随机图模型中,任意两个节点相连的概率都是p, 也就是说CC=p。而在大规模网络中p远远小于1,也就是说ER随机图 不具有聚集特性。 图. 30节点的随机图:(a) p=0; (b) p=0.05; (c) p=0.1; (d) p=0.2

历些毛子代枝大学 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY >随机图模型的结构特征: 平均路径长度L取:可以做一个近似的估算,任取一个点,和它距离为1 的节点数有<心个,距离为2的节点数有<>2个,.,距离为L的节点数 有<k>LR个,见表2-1。表2-1中右列中各项之和为N,有理由相信 N∝<k>LER,即 InN InN LER I<k> In pN 距离 节点数量 0 1 1 <k> 2 <k>2 。。 LER <k >LER 5
第三讲:复杂网络结构模型 5 随机图模型的结构特征: • 平均路径长度LER:可以做一个近似的估算,任取一个点,和它距离为1 的节点数有<k>个,距离为2的节点数有<k> 2个,…,距离为LER的节点数 有< 𝑘 >𝐿𝐸𝑅个,见表2-1。表2-1中右列中各项之和为N,有理由相信 N∝< 𝑘 >𝐿𝐸𝑅 , 即 距离 节点数量 0 1 1 <k> 2 <k>2 … … LER < 𝑘 >𝐿𝐸𝑅 … … 𝐿𝐸𝑅 ∝ 𝑙𝑛𝑁 𝑙𝑛 < 𝑘 > = 𝑙𝑛𝑁 𝑙𝑛 < 𝑝𝑁 >
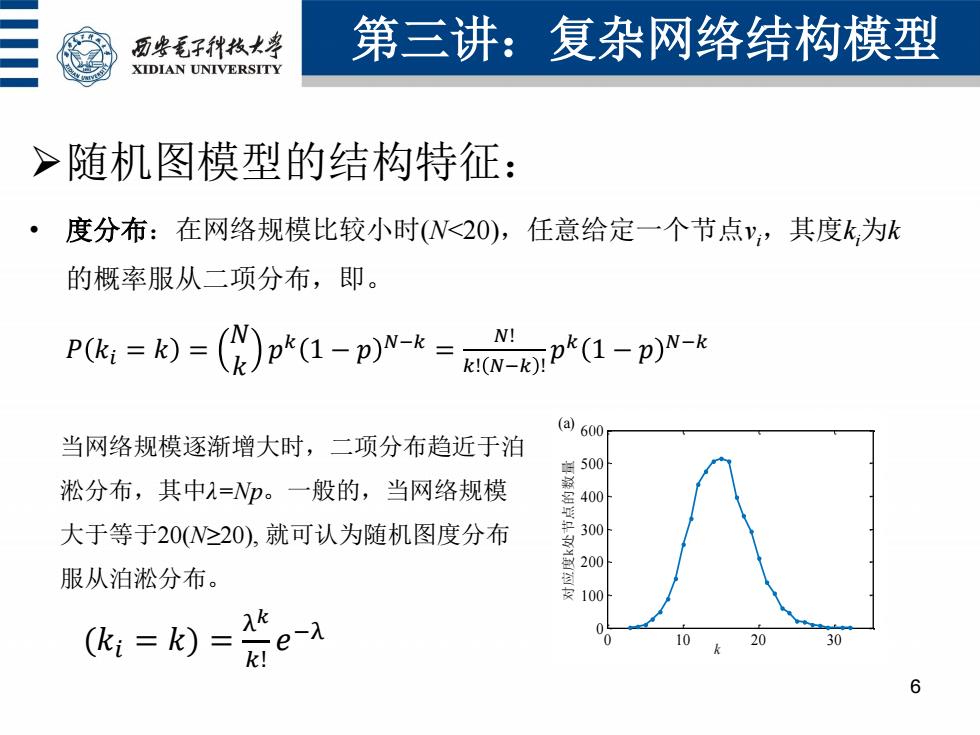
历安毛子代枚大学 第三讲:复杂网络结构模型 XIDIAN UNIVERSITY >随机图模型的结构特征: ·度分布:在网络规模比较小时W<20), 任意给定一个节点y,其度k为k 的概率服从二项分布,即。 Pk=)=((仪p*1-p0w-=1-pw-t (a600 当网络规模逐渐增大时,二项分布趋近于泊 淞分布,其中=p。一般的,当网络规模 大于等于20W>20),就可认为随机图度分布 20 服从泊淞分布。 100 (飞:=k)= Ak e 10 20 6
第三讲:复杂网络结构模型 6 随机图模型的结构特征: • 度分布:在网络规模比较小时(N<20),任意给定一个节点vi,其度ki为k 的概率服从二项分布,即。 𝑃 𝑘𝑖 = 𝑘 = 𝑁 𝑘 𝑝 𝑘 1 − 𝑝 𝑁−𝑘 = 𝑁! 𝑘! 𝑁−𝑘 ! 𝑝 𝑘 1 − 𝑝 𝑁−𝑘 (𝑘𝑖 = 𝑘) = λ 𝑘 𝑘! 𝑒 −λ 当网络规模逐渐增大时,二项分布趋近于泊 淞分布,其中λ=Np。一般的,当网络规模 大于等于20(N≥20), 就可认为随机图度分布 服从泊淞分布。 0 10 20 30 0 100 200 300 400 500 600 k 对应度k处节点的数量 (a)