核心重难探究 知识点一:圆周角定理 【例1】如图,点A,B,C在⊙O上,∠B=60°, OP⊥AC于点P,OP=23,则⊙O的半径为A). A.4v3 B.6v3 B C.8 D.12 思路点拨:先利用圆周角定理根据∠B=60°求出∠AOC,再由 等腰三角形的性质 ,根据 的长得出OA 的长,即为圆O的半径 导航页
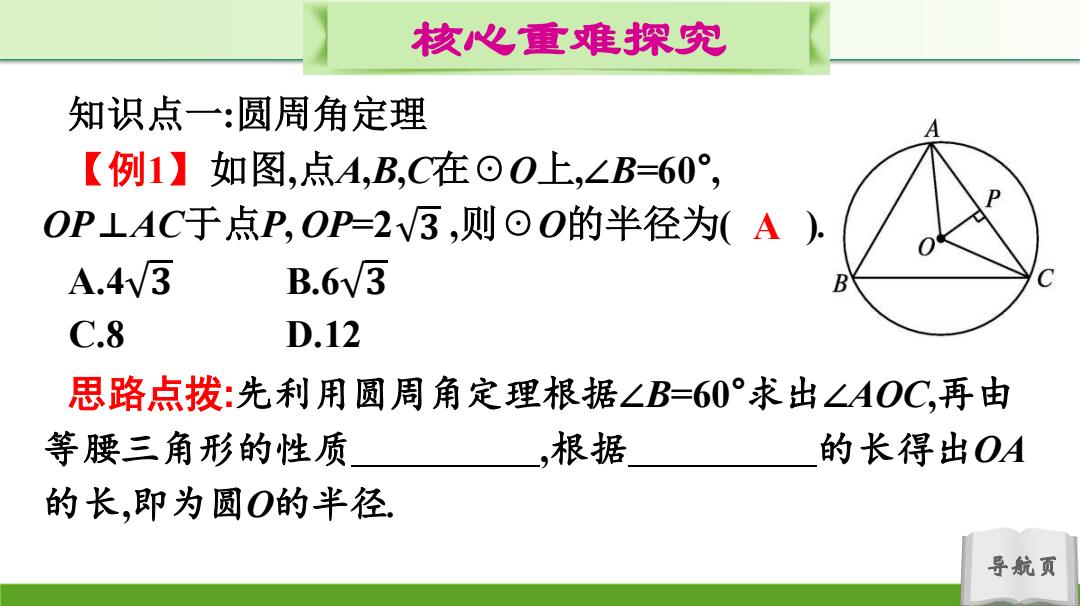
导航页 核心重难探究 知识点一:圆周角定理 【例1】如图,点A,B,C在☉O上,∠B=60° , OP⊥AC于点P, OP=2 ,则☉O的半径为( ). A.4 𝟑 B.6 𝟑 C.8 D.12 𝟑 思路点拨:先利用圆周角定理根据∠B=60°求出∠AOC,再由 等腰三角形的性质 ,根据 的长得出OA 的长,即为圆O的半径. A

核心重难探究 【方法归纳】 利用圆周角定理,知道圆周角的度数可求同弧所对圆心角的 度数:知道圆心角的度数可求同弧所对圆周角的度数 导航页
导航页 核心重难探究 【方法归纳】 利用圆周角定理,知道圆周角的度数可求同弧所对圆心角的 度数;知道圆心角的度数可求同弧所对圆周角的度数