程序运行结果如图5.4所示。 92 9 2 10 15 20 10 15 20 图5.4确定性问题梯度校正参数辨识 仿真(被辨识参数的个数为3) 0. 1.5 25 16
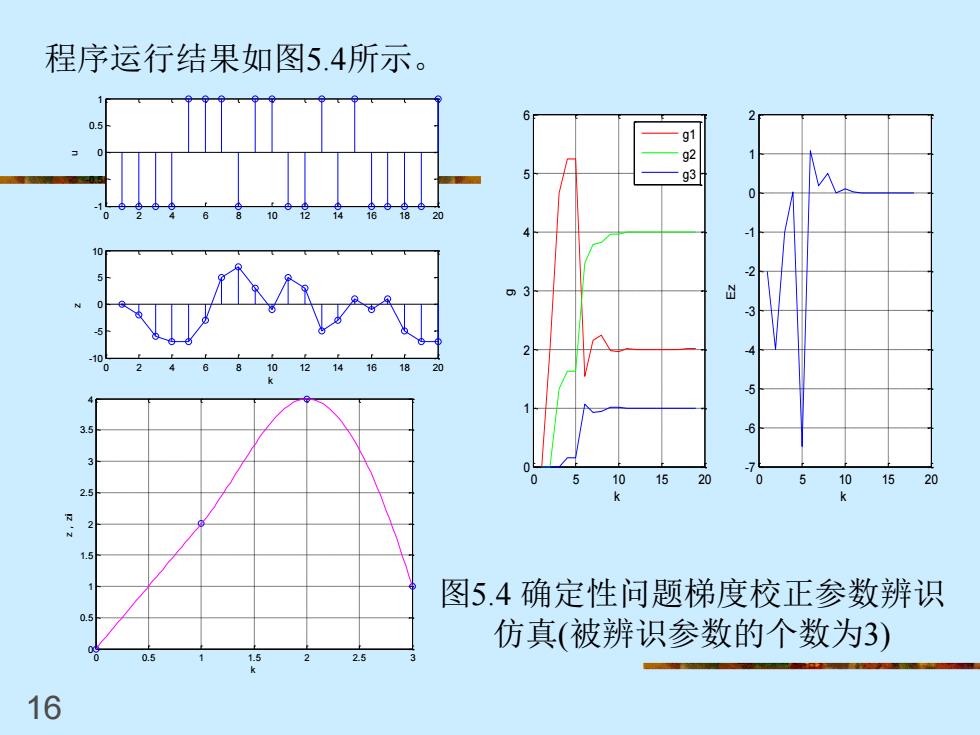
16 程序运行结果如图5.4所示。 0 2 4 6 8 10 12 14 16 18 20 -1 -0.5 0 0.5 1 u 0 2 4 6 8 10 12 14 16 18 20 -10 -5 0 5 10 z k 0 5 10 15 20 0 1 2 3 4 5 6 k g g1 g2 g3 0 5 10 15 20 -7 -6 -5 -4 -3 -2 -1 0 1 2 k Ez 0 0.5 1 1.5 2 2.5 3 0 0.5 1 1.5 2 2.5 3 3.5 4 k z,zi 图5.4 确定性问题梯度校正参数辨识 仿真(被辨识参数的个数为3)

图5.4表明,递推到第10步时,被辨识参数基本上达到了稳定 状态,即 g1→2,g2→4,8→1 此时系统的输出与模型的输出误差也基本达到稳定状态,即 E2z→0 由于被辨识参数的个数较少,递推校正算法的收敛性比较好, 也就是说,输入输出的观测数据量已足够。 为了充分地显示出系统的脉冲响应,可以增加被辨识参数的 个数。一般地,在观测数据量一定的情况下,随着被辨识参数 的个数的增加,梯度校正辨识算法的收敛性变差,这是由于观 测数据不足,递推步数有限造成的。因此观测数据量应随着被 辨识参数的个数的增加而增加。 17
17 图5.4表明,递推到第10步时,被辨识参数基本上达到了稳定 状态,即 ˆ 2, g1 → ˆ 4, g2 → ˆ 1, g3 → 此时系统的输出与模型的输出误差也基本达到稳定状态,即 Ez →0 由于被辨识参数的个数较少,递推校正算法的收敛性比较好, 也就是说,输入输出的观测数据量已足够。 为了充分地显示出系统的脉冲响应,可以增加被辨识参数的 个数。一般地,在观测数据量一定的情况下,随着被辨识参数 的个数的增加,梯度校正辨识算法的收敛性变差,这是由于观 测数据不足,递推步数有限造成的。因此观测数据量应随着被 辨识参数的个数的增加而增加