
设估计的参数误差为)=a,-,如果ak)与hk)不相交, 则不管参数估计的初始值如何选择,参数估计值) 总是大范围一致渐进收敛的,既有 lim8k)=0。 11
11 设估计的参数误差为 (k) (k) ˆ ~ = 0 − (k ) ~ ,如果 与 h(k) 不相交, 则不管参数估计的初始值如何选择,参数估计值 (k ) ˆ 总是大范围一致渐进收敛的,既有 ( ) 0 0 ˆ lim = → k k

5.1.2脉冲响应梯度校正辨识及其MATLAB仿真 例5.1某线性时不变SIS0系统如图5.2所示。 u(k) =(k) G(s) 图5.2单输入单输出系统 根据卷积定理,系统的输出()与输入序列k-)-2),-) 的关系可表示为 zk)=立gk-) 7-1 式中,81,82,…,8N组成系统的脉冲响应。 12
12 5.1.2 脉冲响应梯度校正辨识及其MATLAB仿真 例5.1某线性时不变SISO系统如图5.2所示。 G(s) z(k ) u(k ) 图5.2 单输入单输出系统 根据卷积定理,系统的输出 z(k) 与输入序列 u(k −1), u(k −2), u(k − N) , 的关系可表示为 ( ) ( ) = = − N i i z k g u k i 1 式中, g g gN , , , 1 2 组成系统的脉冲响应

系统在伪随机码输入作用下的输出响应如表5.1所示。 表5.1输入输出数据 k012345678910111213141516171819. k11-11111111111111-1-111. z)026773573153531115-77… 利用这些数据辨识系统的脉冲响应,当N取3时,有 d)=立8ak- 13
13 系统在伪随机码输入作用下的输出响应如表5.1所示。 表5.1 输入输出数据 k 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 … u(k) -1 -1 -1 -1 1 1 1 -1 1 1 -1 -1 1 -1 1 -1 -1 -1 -1 1 … z(k) 0 -2 -6 -7 -7 -3 5 7 3 -1 5 3 -5 -3 1 -1 1 -5 -7 -7 … 利用这些数据辨识系统的脉冲响应,当N取3时,有 ( ) ( ) = = − 3 i 1 i z k g u k i

hk)=[u(k-1,u(k-2),uk-3 令 g=[81,g2,g3Y 若系统的真实脉冲响应记作8,则有 z(k)=h"(k)go 脉冲响应估计值)的递推算式可表示为 (k+1)=(k)+R(k)h(k)=(k)-h"(k)( 式中,脉冲响应估计值的初始值取ξ=0,权矩阵取值如式(⑤.26)。 R(k)= diag[a,(k),a(k),k】 (5.26) ∑) 14
14 令 ( ) ( ) ( ) ( ) = = − − − T T g g g g h k u k u k u k 1 2 3 , , 1 , 2 , 3 若系统的真实脉冲响应记作 0 g ,则有 ( ) ( )g0 z k h k T = 脉冲响应估计值 g ˆ(k) 的递推算式可表示为 g(k ) g(k) R(k)h(k)z(k) h (k)g(k) T ˆ +1 = ˆ + − ˆ 式中,脉冲响应估计值的初始值取 g ˆ = 0 ,权矩阵取值如式(5.26)。 ( ) ( ) ( ) diag (k ) (k ) (k ) k h k R k N i i i 1 2 3 1 2 , , 1 = = (5.26)
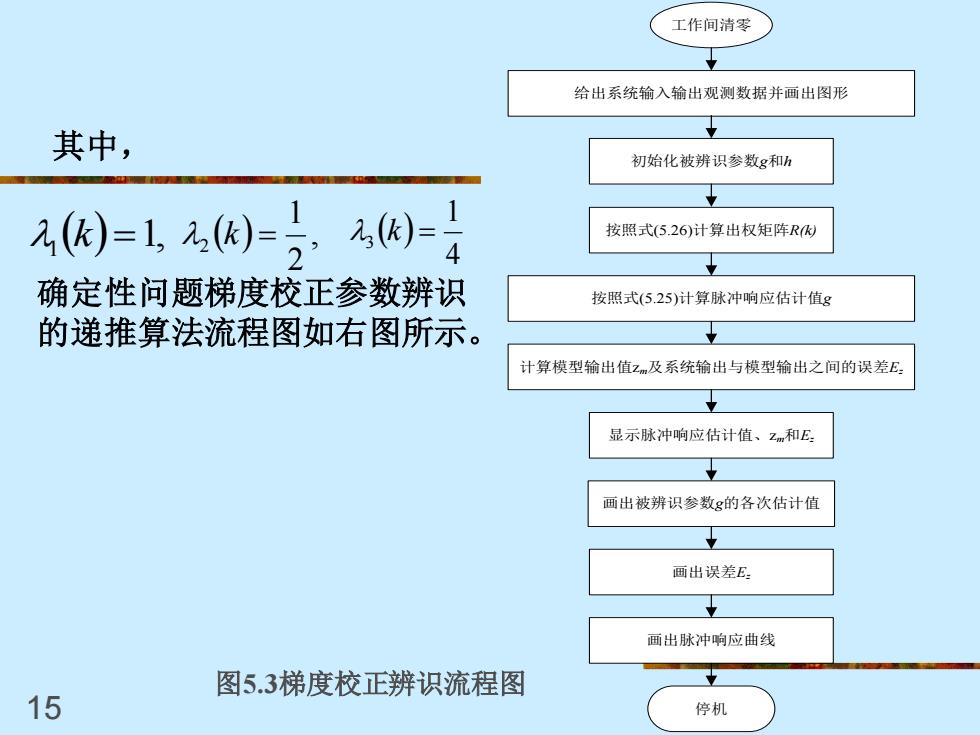
工作间清零 给出系统输入输出观测数据并画出图形 其中, 立 初始化被辨识参数g和h 2风)=1)=))-月 按照式(5.26)计算出权矩阵R) 确定性问题梯度校正参数辨识 按照式(5.25)计算脉冲响应估计值g 的递推算法流程图如右图所示。 计算模型输出值zm及系统输出与模型输出之间的误差E: 显示脉冲响应估计值、Zm和E 画出被辨识参数g的各次估计值 画出误差E 画出脉冲响应曲线 图5.3梯度校正辨识流程图 15 停机
15 其中, ( ) 1, 1 k = ( ) , 2 1 2 k = ( ) 4 1 3 k = 确定性问题梯度校正参数辨识 的递推算法流程图如右图所示。 给出系统输入输出观测数据并画出图形 工作间清零 初始化被辨识参数g和h 按照式(5.26)计算出权矩阵R(k) 按照式(5.25)计算脉冲响应估计值g 计算模型输出值zm及系统输出与模型输出之间的误差Ez 显示脉冲响应估计值、zm和Ez 画出被辨识参数g的各次估计值 画出误差Ez 画出脉冲响应曲线 停机 图5.3梯度校正辨识流程图