
从图可见,它是一个多输入、单输出的非线性元件,其输入输出 关系可描述为: =∑ (6.1) =1 y=f(1) 其中x=1,2,…,m) 是从其它细胞传来的输入信号,B为阙值, 权系数O表示连接的强度,说明突触的负载。f(x)称为激发函数 或作用函数,其非线性特性可用阈值型、分段线性型和连续型激 发函数近似。 为了方便,有时将-B也看成是对应恒等于1的输入的权值,(6.1) 式的和式变成: (6.2) 其中w=-0,x,=1 6
6 从图可见,它是一个多输入、单输出的非线性元件,其输入输出 关系可描述为: I w x y f I j j j n = − = = 1 ( ) (6.1) 其中 是从其它细胞传来的输入信号, 为阈值, 权系数 表示连接的强度,说明突触的负载。 称为激发函数 或作用函数,其非线性特性可用阈值型、分段线性型和连续型激 发函数近似。 为了方便,有时将- 也看成是对应恒等于1的输入的权值,(6.1) 式的和式变成: xj ( j = 1,2, ,n) wj f (x) = = n j j j I w x 0 (6.2) 其中 0 0 w x = − = , 1

6.1.2 激发函数 常用的激发函数如图6.2示。图中(a)和(b)为阈值型函数;(c)为饱和 型函数:(d是双曲型函数或称为对称的sigoid函数)=m) (e)是sid函数,)1+通常情况下B取1, (f)是高斯函数, -m“c是高斯函数中心值,c为0时函数以纵轴对称,b是高 斯函数尺度因子,b确定高斯函数的宽度。 】 (x 图6.2激发函数
7 常用的激发函数如图6.2示。图中(a)和(b)为阈值型函数;(c)为饱和 型函数;(d)是双曲型函数或称为对称的sigmoid函数 ; (e)是sigmoid函数, 通常情况下 取1; (f)是高斯函数, c是高斯函数中心值,c为0时函数以纵轴对称,b是高 斯函数尺度因子,b确定高斯函数的宽度。 6.1.2 激发函数 I I e e f x x − − + − = = 1 1 ( ) tanh( ) I e f x − + = 1 1 ( ) − = 2 2 ( ) ( ) exp b I c f x -1 -1 (a) (b) (c) 1 0 0 0 1 1 1 0 -1 1 0.5 0 -1 0 1 x x x x x x f(x) f(x) f(x) f(x) f(x) f(x) (d) (e) (f) 图6.2激发函数

6.1.3神经网络模型分类 神经网络是由大量的神经元广泛连接成的网络。根 据连接方式的不同,神经网络可以分为两大类:无 反馈的前向网络和相互连接型网络(包括反馈网络) 如图6.3所示。前向网络有输入层、隐含层(简称 隐层也称中间层)和输出层,隐层可以有若干层, 每一层的神经元只接受前一层神经元的输出。而相 互结合型网络的神经元相互之间都可能有连接,因 此,输入信号要在神经元之间反复往返传递,从某 一初态开始,经过若干次的变化,渐渐趋于某一稳 定状态或进入周期振荡等其它状态。 8
8 6.1.3神经网络模型分类 神经网络是由大量的神经元广泛连接成的网络。根 据连接方式的不同,神经网络可以分为两大类:无 反馈的前向网络和相互连接型网络(包括反馈网络) 如图6.3所示。前向网络有输入层、隐含层(简称 隐层也称中间层)和输出层,隐层可以有若干层, 每一层的神经元只接受前一层神经元的输出。而相 互结合型网络的神经元相互之间都可能有连接,因 此,输入信号要在神经元之间反复往返传递,从某 一初态开始,经过若干次的变化,渐渐趋于某一稳 定状态或进入周期振荡等其它状态
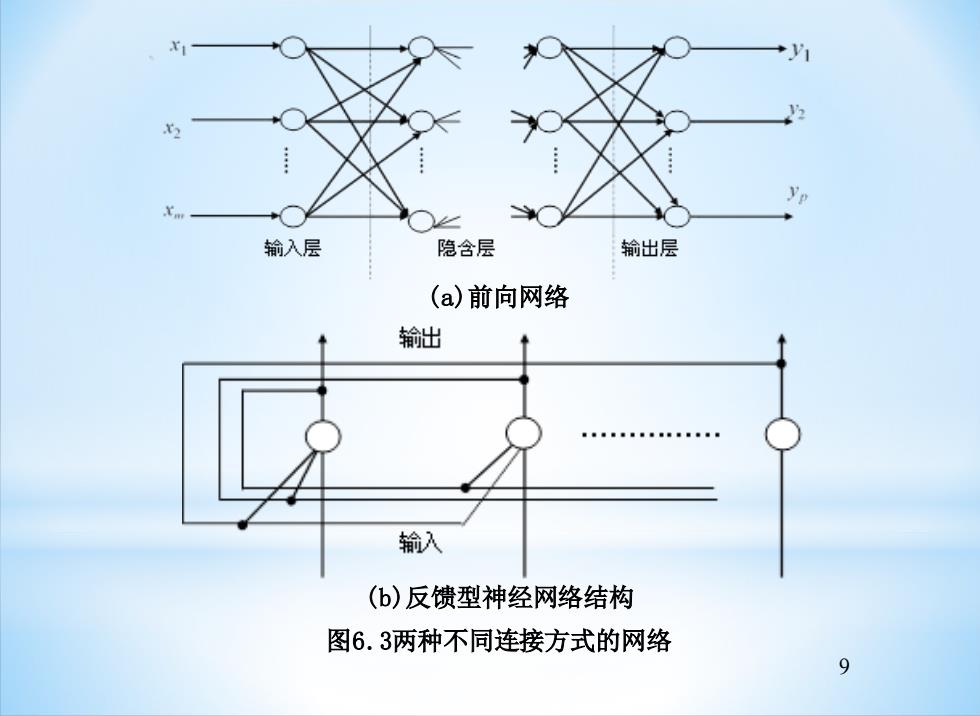
输入层 隐含层 输出层 (a)前向网络 输出 输入 (b)反馈型神经网络结构 图6.3两种不同连接方式的网络
9 (a)前向网络 (b)反馈型神经网络结构 图6.3两种不同连接方式的网络

6.1.4神经网络学习方法 1)学习方法的种类 神经网络学习方法有多种。若按学习规则,网络的学习可分为三 类:相关规则,即仅仅根据连接间的激活水平改变权值;纠错规 则,即依赖关于输出节点的外部反馈来改变权系数;无教师学习 规则,即学习表现为自适应于输入空间的检测规则。 (1)相关规则相关规则常用于自联想网络,执行特殊记忆状态的 死记式学习,也属于无教师的学习。Hopfied网络就是如此,所采 用的是修正的Hebb规则。 (2)纠错规则从方法上等效于梯度下降法,通过在局部最大改善 的方向上逐步地进行修正,力图达到表示函数功能的全局解。感 知器即使用纠错规则:①若一节点的输出正确,一切不变;②若 输出本应为0而为1,则相应的权值减小;③若输出应为1而为0, 则权值增加。 10
10 6.1.4神经网络学习方法 1)学习方法的种类 神经网络学习方法有多种。若按学习规则,网络的学习可分为三 类:相关规则,即仅仅根据连接间的激活水平改变权值;纠错规 则,即依赖关于输出节点的外部反馈来改变权系数;无教师学习 规则,即学习表现为自适应于输入空间的检测规则。 (1)相关规则相关规则常用于自联想网络,执行特殊记忆状态的 死记式学习,也属于无教师的学习。Hopfied网络就是如此,所采 用的是修正的Hebb规则。 (2)纠错规则从方法上等效于梯度下降法,通过在局部最大改善 的方向上逐步地进行修正,力图达到表示函数功能的全局解。感 知器即使用纠错规则:①若一节点的输出正确,一切不变;②若 输出本应为0而为1,则相应的权值减小;③若输出应为1而为0, 则权值增加