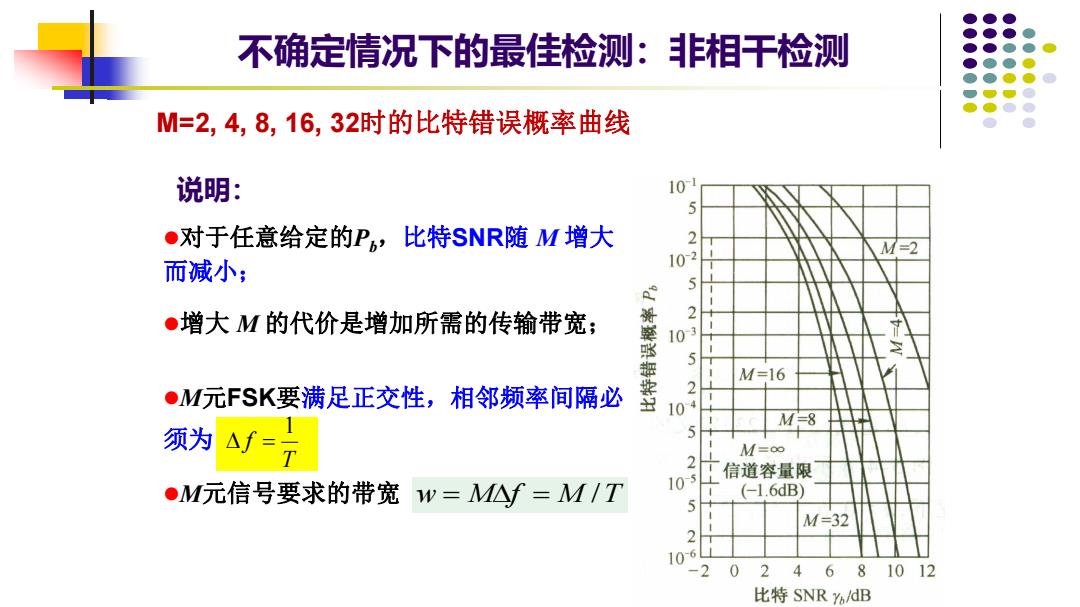
不确定情况下的最佳检测:非相干检测 M=2,4,8,16,32时的比特错误概率曲线 说明: 10- 5 ●对于任意给定的Pb,比特SNR随M增大 2 M=2 而减小; 102 5 ●增大M的代价是增加所需的传输带宽; 2 103 5 M=16 2 ●M元FSK要满足正交性,相邻频率间隔必 104 须为f=月 M=8 5 M=o∞ 2 信道容量限 ●M元信号要求的带宽w=M△f=M/T 105L (-1.6dB) 5 M=32 2 106LL -20 2 4 6 81012 比特SNRY%/dB
⚫对于任意给定的Pb,比特SNR随 M 增大 而减小; ⚫增大 M 的代价是增加所需的传输带宽; 6 不确定情况下的最佳检测:非相干检测 w = Mf = M /T 说明: M=2, 4, 8, 16, 32时的比特错误概率曲线 T f 1 = ⚫M元FSK要满足正交性,相邻频率间隔必 须为 ⚫M元信号要求的带宽

4.5.4相关二进制信号包络检测 的错误概率 7
7 4.5.4 相关二进制信号包络检测 的错误概率

不确定情况下的最佳检测:非相干检测 二进制等能量相关信号包络检测的性能 (p*0) 两个信号相关时,解调器输出: (复随机变量) h=2εcos0+nc+j2εsinp+n,) r2 =28p cos(o-do)+ne+j(28psin(o-a)+ns) 检测器:依据包络R1=、R2=r2进行判决(这两个包络是相关的) 假定发送信号是s),如同前面推导,R1、R2的边缘PDF均服从 Rice分布: R>0 P(R)=28No 0 R<0 其中m=1,2,B,=2s,B2=2Ep 8
8 不确定情况下的最佳检测:非相干检测 2 cos( ) (2 sin( ) ) 2 cos (2 sin ) 2 0 2 0 2 1 1 1 c s c s r n j n r n j n = − + + − + = + + + 2 2 0 0 0 0 exp( ) ( ) 0 ( ) 2 4 2 0 0 m m m m m m m m R R R I R P R N N N R + − = 其中 m =1,2, 1 = 2, 2 = 2 二进制等能量相关信号包络检测的性能 两个信号相关时,解调器输出: (复随机变量) 检测器:依据包络 R1=|r1 |、R2=|r2 | 进行判决(这两个包络是相关的) 假定发送信号是s1 (t),如同前面推导,R1、R2的边缘PDF均服从 Rice分布: ( ≠ 0)

不确定情况下的最佳检测:非相干检测 因p0,信号非正交,R1与R2统计相关,错误概率:(通过计算二重积分得到) B=PR>R)=P心,: R1,R2的联合PDF 方法二: 错误概率: P=P(R>R)=P(R2>R2)=P(R2-R2>0) 包络检波 平方律检波 经推导: (略) P=,(a,b)-e-a+b21(ab) 其中:a= 1-V1-lp) 9
9 不确定情况下的最佳检测:非相干检测 1 2 1 1 2 1 2 0 ( ) ( , ) b x P P R R P x x dx dx = = 错误概率: ( ) ( ) ( 0) 2 1 2 2 2 1 2 Pb = P R2 R1 = P R2 R = P R − R 方法二: ( ) 2 1 ( , ) 0 ( )/ 2 1 2 2 P Q a b e I ab a b b − + = − R1 , R2 的联合PDF 包络检波 平方律检波 其中: 2 0 (1 1 ) 2 b b N (1 1 ) = + + 2 2 0 = − − N a b 经推导: (略) 因 ≠0,信号非正交,R1与R2统计相关,错误概率:(通过计算二重积分得到)
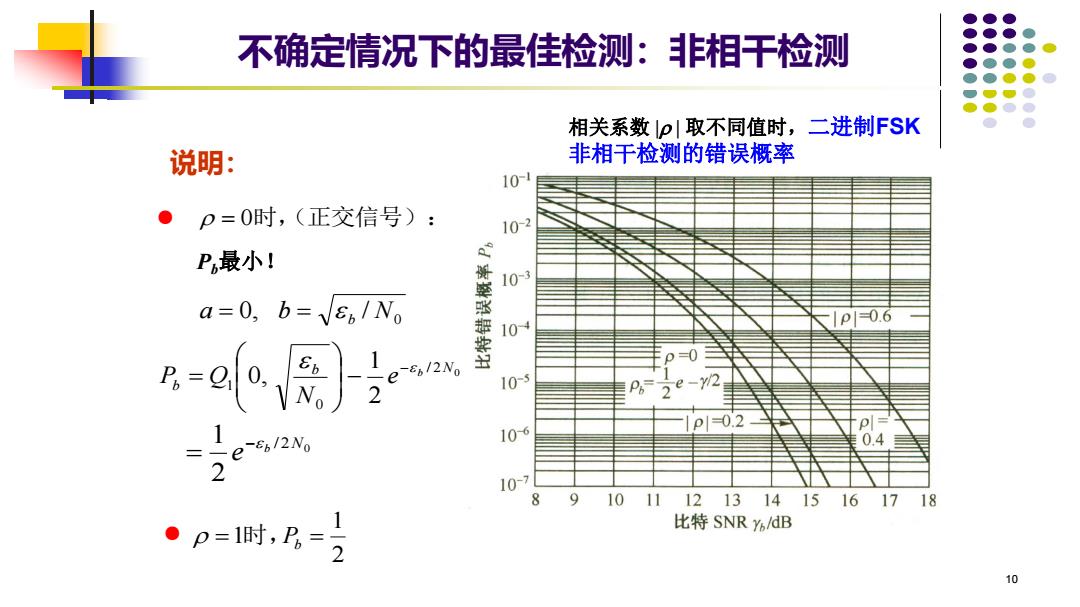
不确定情况下的最佳检测:非相干检测 相关系数p取不同值时,二进制FSK 说明: 非相干检测的错误概率 10 p=0时,(正交信号): ● 10-2 P最小I 10- a=0,b=s/No 104 、1p=0.6 a-alo 0=0 10-3 Po=2e-y2 p|=0.2 2e2 109 0.4 10-7 8 9.1011 12131415161718 0p=1时,P,= 比特SNR Yh/dB 2 10
10 0 a = 0, b = b / N 2 0 / 0 1 2 1 0, b N b b e N P Q − − = = 0时,(正交信号): 2 0 / 2 1 b N e − = 2 1 =1时,Pb = 说明: ● ● 相关系数 | | 取不同值时,二进制FSK 非相干检测的错误概率 不确定情况下的最佳检测:非相干检测 Pb最小!