
已知:P=1000N,各杆重不计。求:三根杆所受力。 解:各杆均为二力杆,取球铰O为研究对象 F =0 B之4 45 45 ∑ =0 G ∑ =0
已知:P=1000N ,各杆重不计。 求:三根杆所受力。 解:各杆均为二力杆,取球铰O为研究对象 = = = 0 0 0 i z i y i x F F F
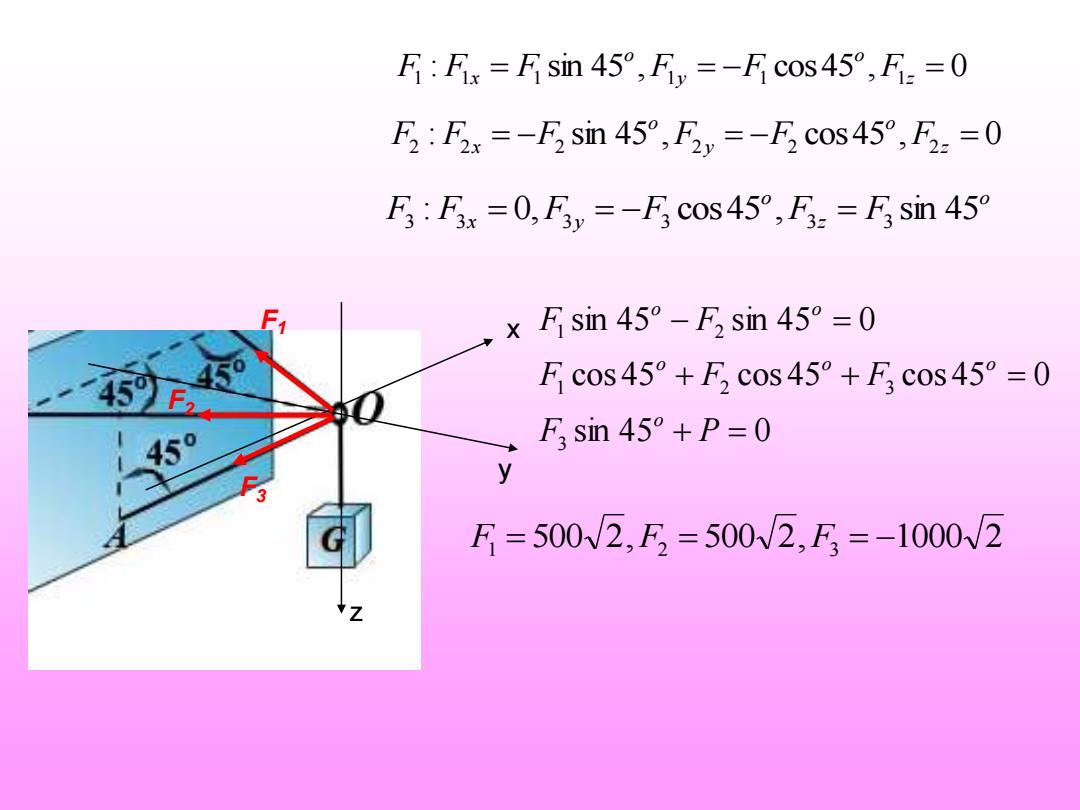
F:Fx=Fsin45°,Ey=-Fcos45°,F.=0 F:F2x=-Fsin45°,Fy=-Fcos45°,F.=0 F:F3x=0,F3v=-Fcos45°,F.=F3sin45° ,x Fsin45°-Fsm45°=0 Ec0s45°+F,c0s45°+F,c0s45°=0 F sin 45+P=0 →y F=500W2,E=500W2,F=-1000W2
xy z F 1 F2 F3 1 : 1 = 1 sin 45 , 1 = − 1 cos45 , 1z = 0 o y o F F x F F F F 2 : 2 = − 2 sin 45 , 2 = − 2 cos45 , 2 z = 0 o y o F F x F F F F o z o F3 : F3 x = 0,F3 y = − F3 cos45 ,F3 = F3 sin 45 sin 45 0 cos 45 cos 45 cos 45 0 sin 45 sin 45 0 31 2 3 1 2 + = + + = − = F P F F F F F oo o o o o F1 = 500 2,F2 = 500 2,F3 = −1000 2
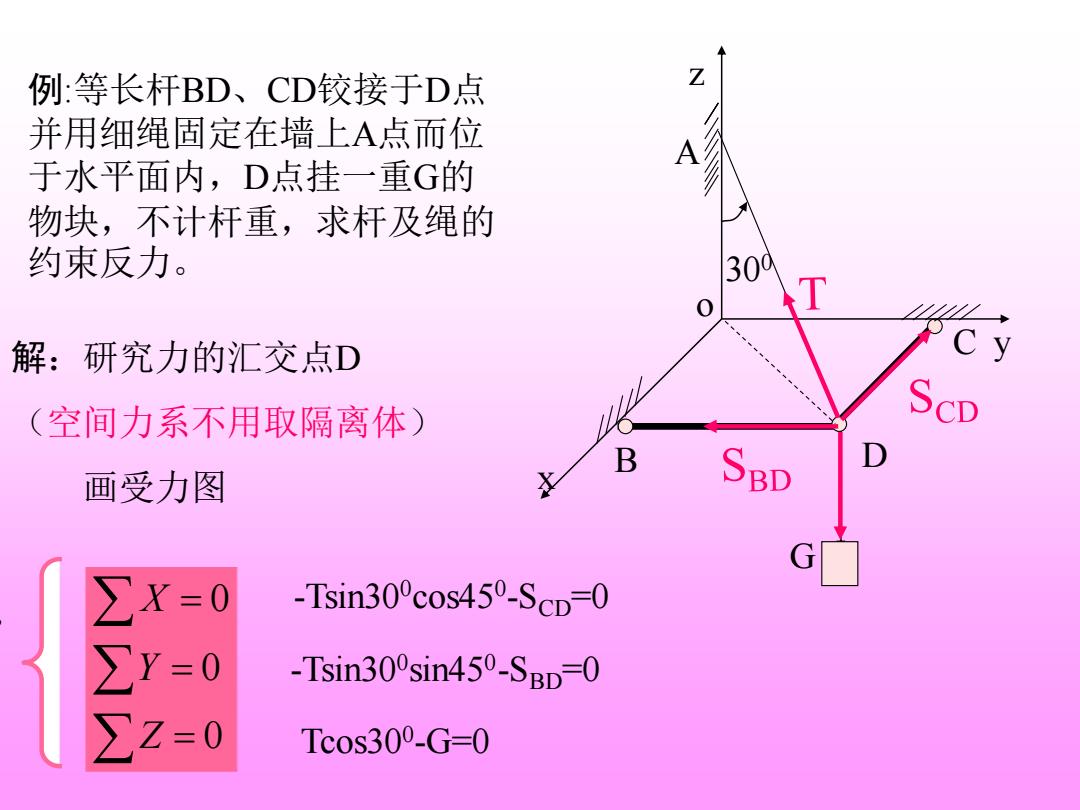
例:等长杆BD、CD铰接于D点 并用细绳固定在墙上A点而位 于水平面内,D点挂一重G的 物块,不计杆重,求杆及绳的 约束反力。 300 0 T 解:研究力的汇交点D C (空间力系不用取隔离体) ScD B 画受力图 ∑X=0 -Tsin300cos450-Scp=0 -Tsin300sin450-SBD-0 Tcos300-G=0
C 300 z y x o B A D G ∴ 0 0 0 = = = Z Y X 例:等长杆BD、CD铰接于D点 并用细绳固定在墙上A点而位 于水平面内,D点挂一重G的 物块,不计杆重,求杆及绳的 约束反力。 -Tsin300cos450 -SCD=0 -Tsin300 sin450 -SBD=0 Tcos300 -G=0 解:研究力的汇交点D (空间力系不用取隔离体) 画受力图
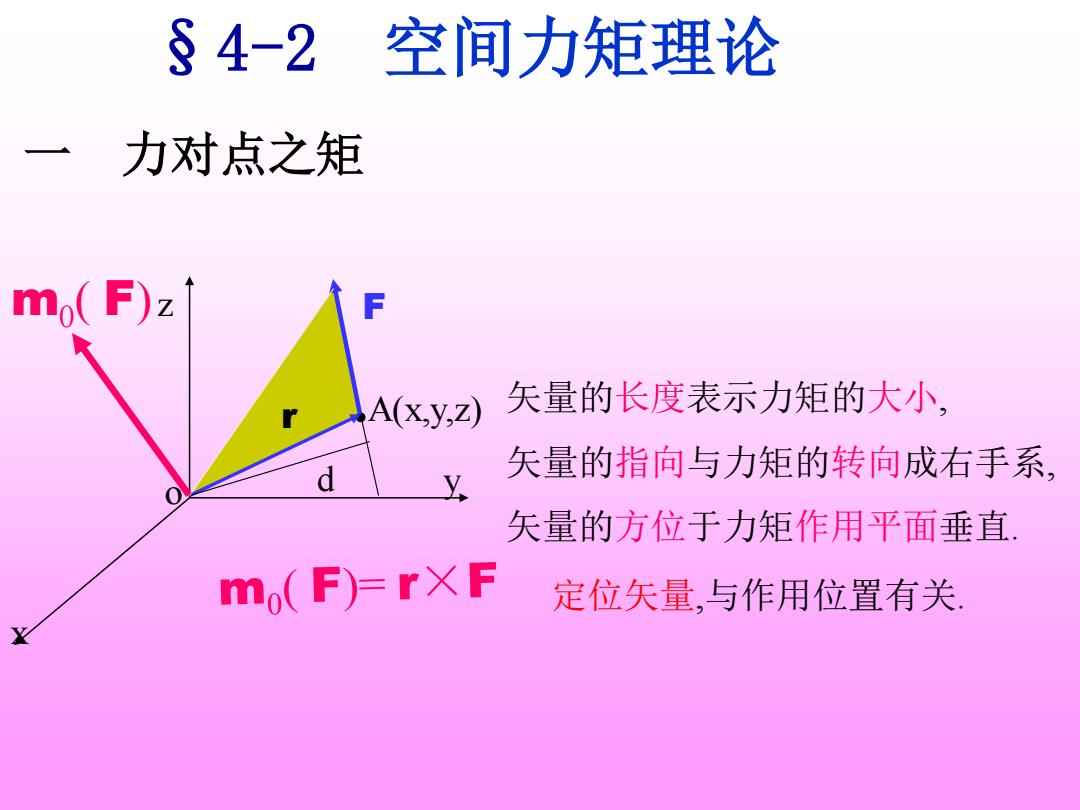
§4-2 空间力矩理论 力对点之矩 mo(F)z A(x,y,z) 矢量的长度表示力矩的大小 d 矢量的指向与力矩的转向成右手系 y 矢量的方位于力矩作用平面垂直 m(F)=rXF 定位矢量,与作用位置有关
§4-2 空间力矩理论 一 力对点之矩 r d z F y x o .A(x,y,z) 矢量的长度表示力矩的大小, 矢量的指向与力矩的转向成右手系, 矢量的方位于力矩作用平面垂直. 定位矢量,与作用位置有关. m0 ( F)
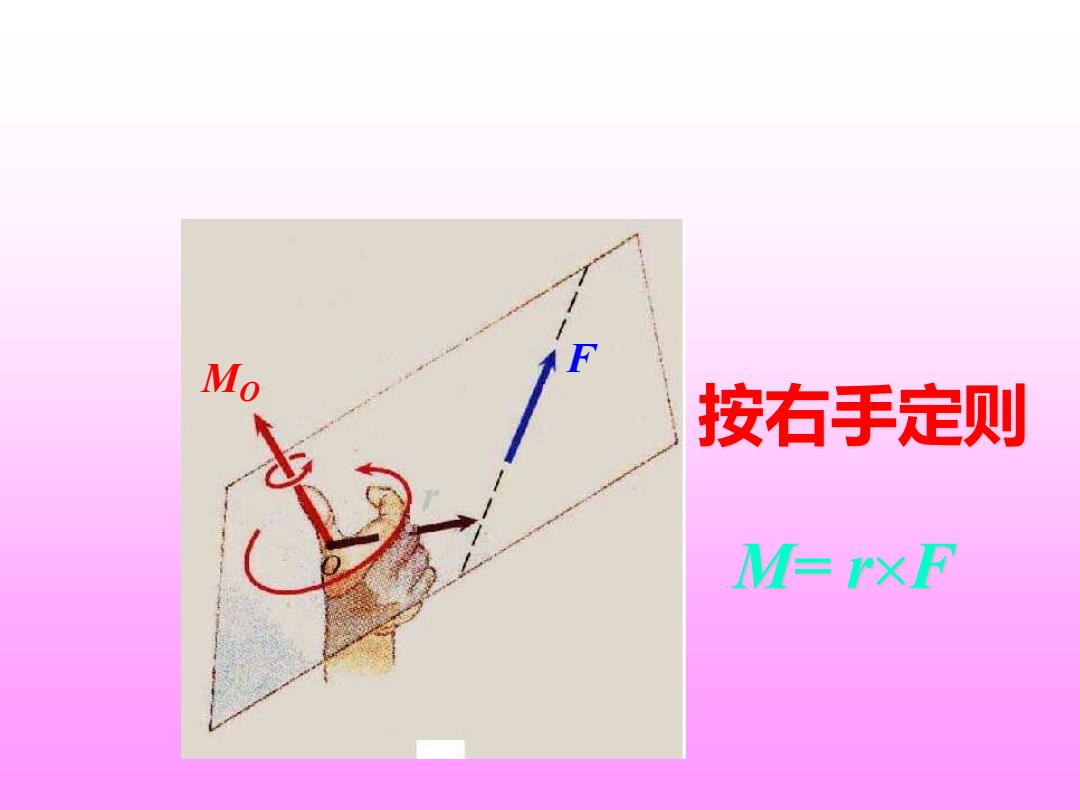
Mo 按右手定则 M=rxF
M= r F 按右手定则 F r MO