
M,(F)=F×F(右手法则) B M ×F=rsin a y 力矩矢与O点的选择有关!,定位矢量
z y x o A B M (F) o α M (F) r F(右手法则) o = S ABO r F F r = = 2 sin 力矩矢与o点的选择有关!,定位矢量
1、力对点矩矢的解析式 Z Z F=Xi+Yj+Zk r=xi+yj+zk mo(F)=rXF Z 0 i j k X X 三 X y X Y Z =(yZ-Zy)i+(ZX -xZ)j+(xY-yX)k
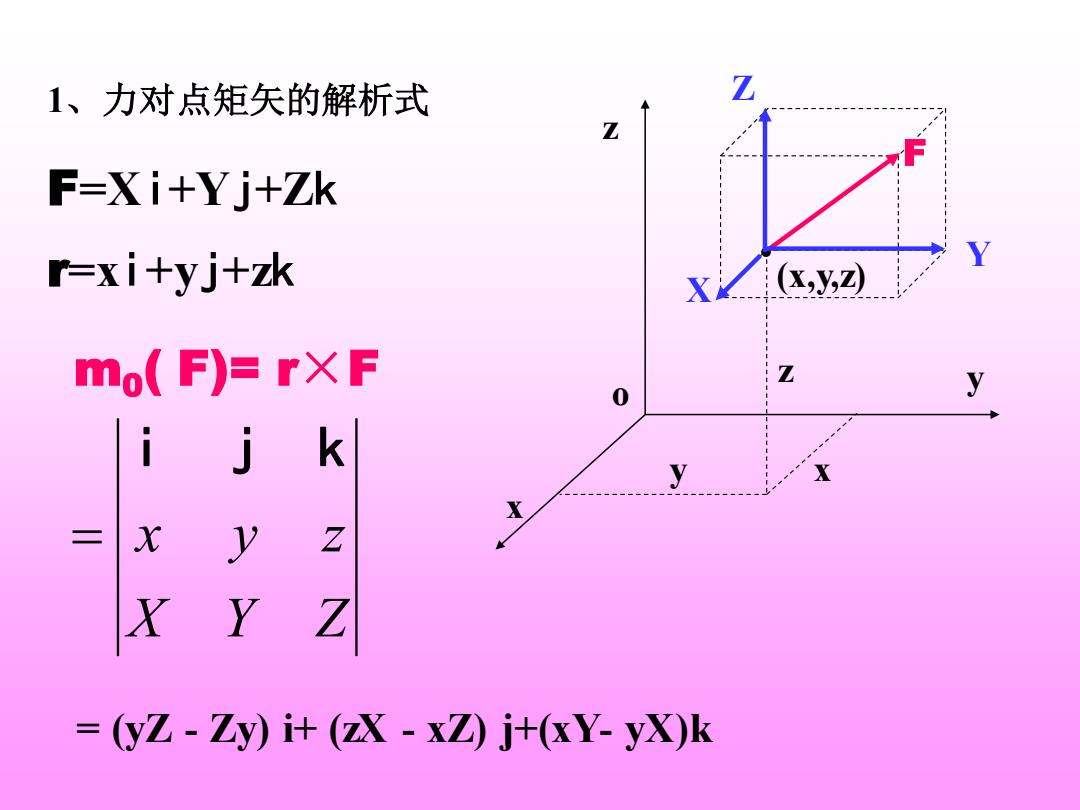
1、力对点矩矢的解析式 F=Xi+Yj+Zk r=xi+yj+zk m0 ( F)= r×F X Y Z x y z i j k = z y x o (x,y,z) . F X Y Z z y x = (yZ - Zy) i+ (zX - xZ) j+(xY- yX)k

二.力对轴之矩 (度量力对绕定轴转动刚体的作用效果) F
二. 力对轴之矩 (度量力对绕定轴转动刚体的作用效果)
力F使物体绕z轴转动的效应称 为力对轴之矩,记为: m(F)F±FxOA =±Fyh 显然:力与轴平行,无矩 h 力与轴相交,无矩 即:力与轴位于同一 B 平面内时,无矩 合力矩定理: 如果力与轴共面: mz(R)=Σmz(F) Mz(F)=0
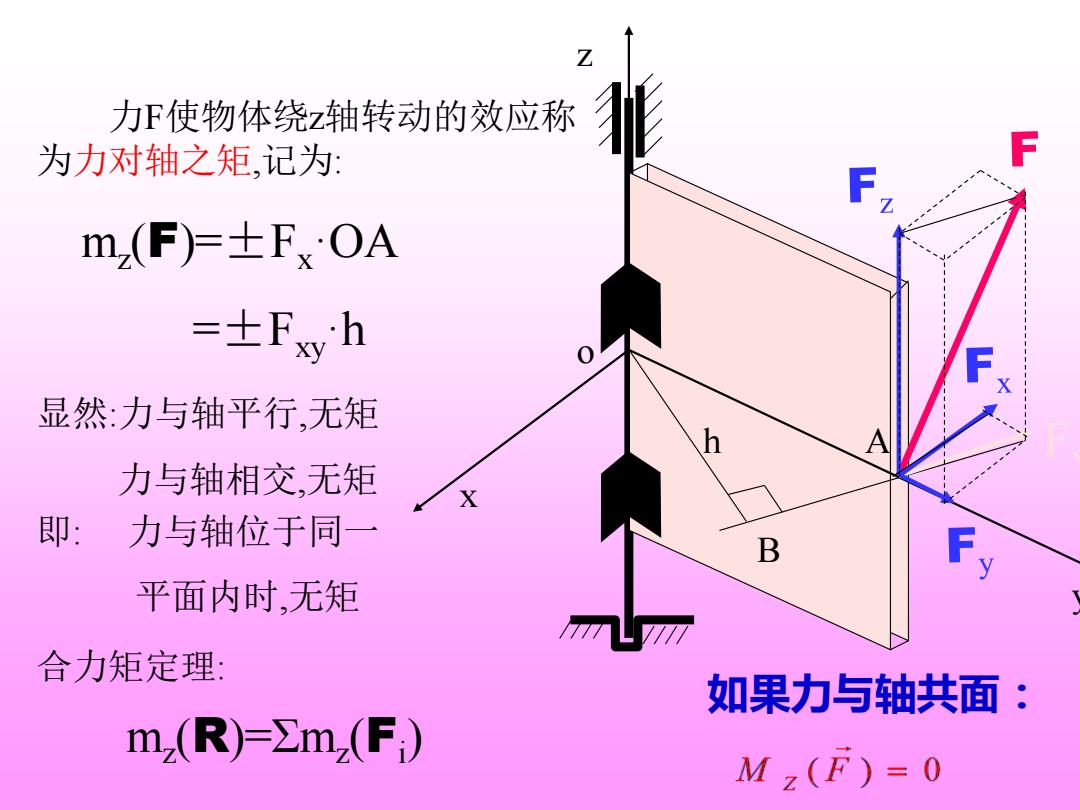
z y 力F使物体绕z轴转动的效应称 为力对轴之矩,记为: mz (F)=±Fx·OA =±Fxy·h o h A x B 显然:力与轴平行,无矩 力与轴相交,无矩 即: 力与轴位于同一 平面内时,无矩 合力矩定理: mz (R)=Σmz (Fi ) 如果力与轴共面: