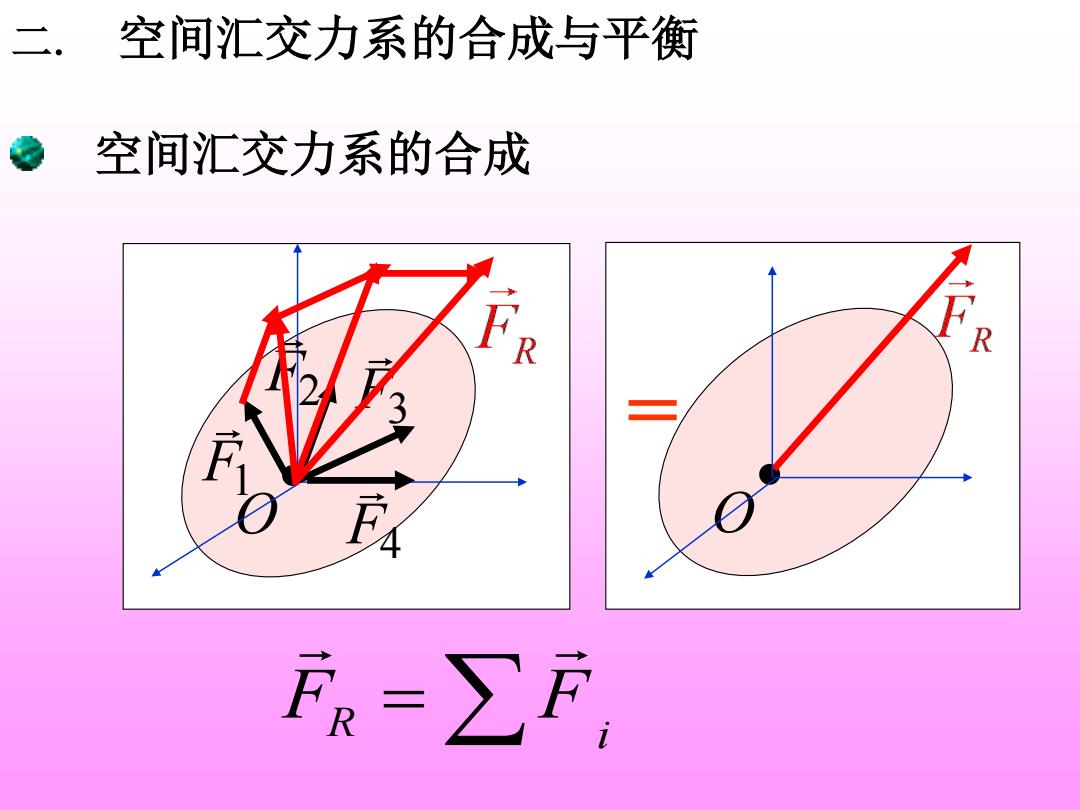
二.空间汇交力系的合成与平衡 空间汇交力系的合成 R R 三 F-∑F
• O F1 F2 F3 F4 二. 空间汇交力系的合成与平衡 空间汇交力系的合成 • O = R i F = F
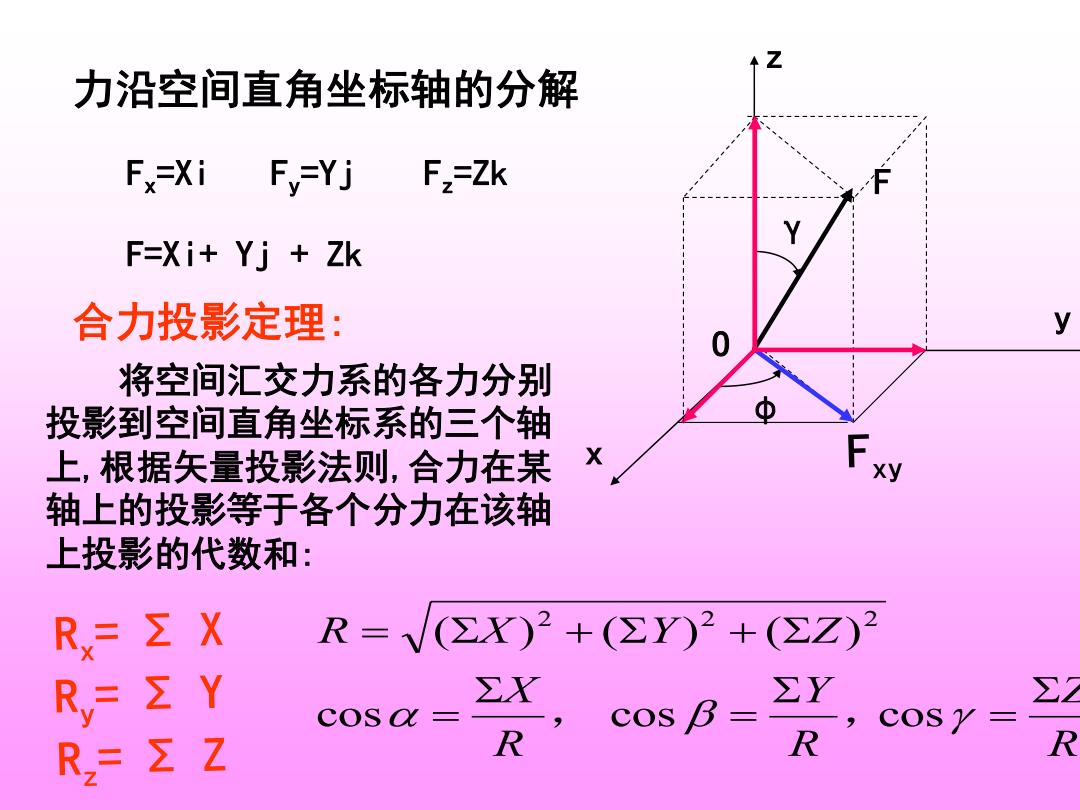
Z 力沿空间直角坐标轴的分解 F,=Xi F=Yj F,=Zk F=Xi+Yj Zk 合力投影定理: y 将空间汇交力系的各力分别 投影到空间直角坐标系的三个轴 上,根据矢量投影法则,合力在某 X y 轴上的投影等于各个分力在该轴 上投影的代数和: R=ΣX R=/(∑X)2+(ΣY2+(∑Z)2 Ry= ΣY ∑X cos B= ΣY ∑2 cosa= R,=ΣZ R R R
O F x γ z y φ 力沿空间直角坐标轴的分解 Fx=Xi Fy=Yj Fz=Zk F=Xi+ Yj + Zk 将空间汇交力系的各力分别 投影到空间直角坐标系的三个轴 上,根据矢量投影法则,合力在某 轴上的投影等于各个分力在该轴 上投影的代数和 : RZ RY RX R X Y Z = = = = + + cos cos cos ( ) ( ) ( ) 2 2 2 , , 合力投影定理 :
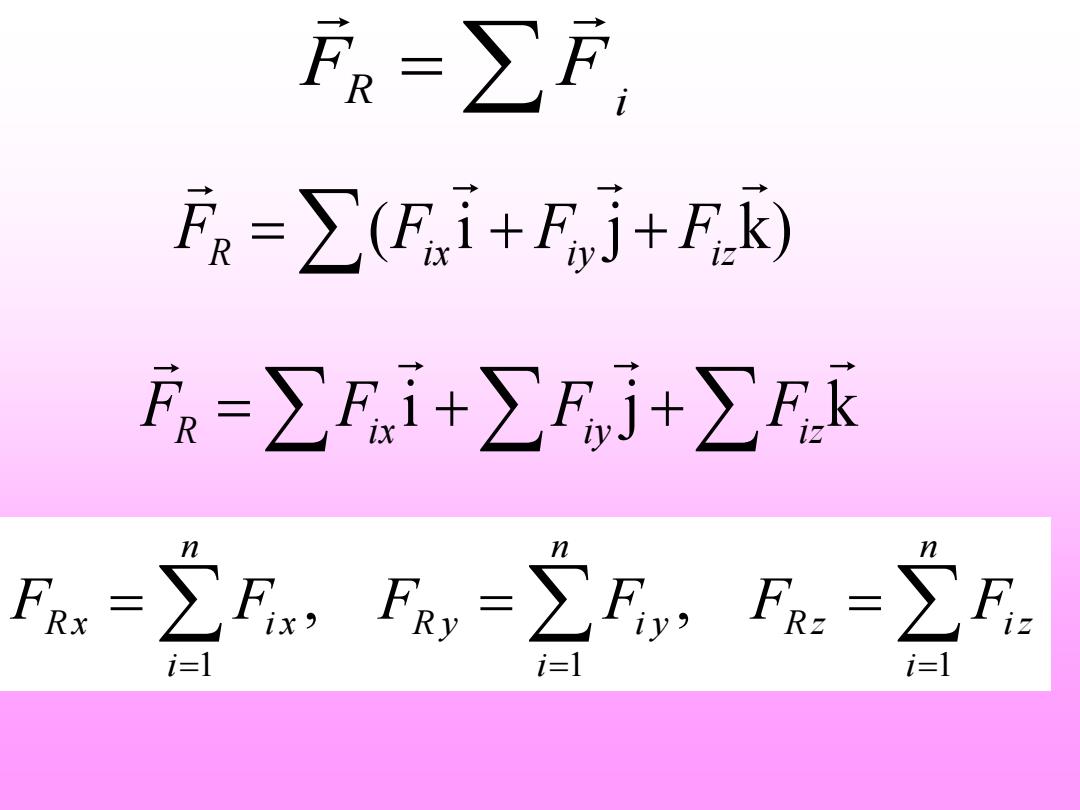
=∑F, F=∑i+Fj+F.k i。=∑Fi+∑Fj+∑F.k F=∑R,-∑F:F=2F i=l i=l i=l
R i F = F ( i j k) FR = Fi x + Fi y + Fi z i j k FR =Fi x +Fi y +Fi z 1 1 1 , , n n n R x i x R y i y R z i z i i i F F F F F F = = = = = =

F=∑F F=2F,F,=2F,F.=∑r i=l i=1 i=l 空间汇交力系的平衡 F=∑F=0 r.-0,立r,-0,∑r.-0 n i=l i=1 i=1
R i F = F 1 1 1 , , n n n R x i x R y i y R z i z i i i F F F F F F = = = = = = 空间汇交力系的平衡 1 1 1 0, 0, 0 n n n i x i y i z i i i F F F = = = = = = = = 0 R i F F
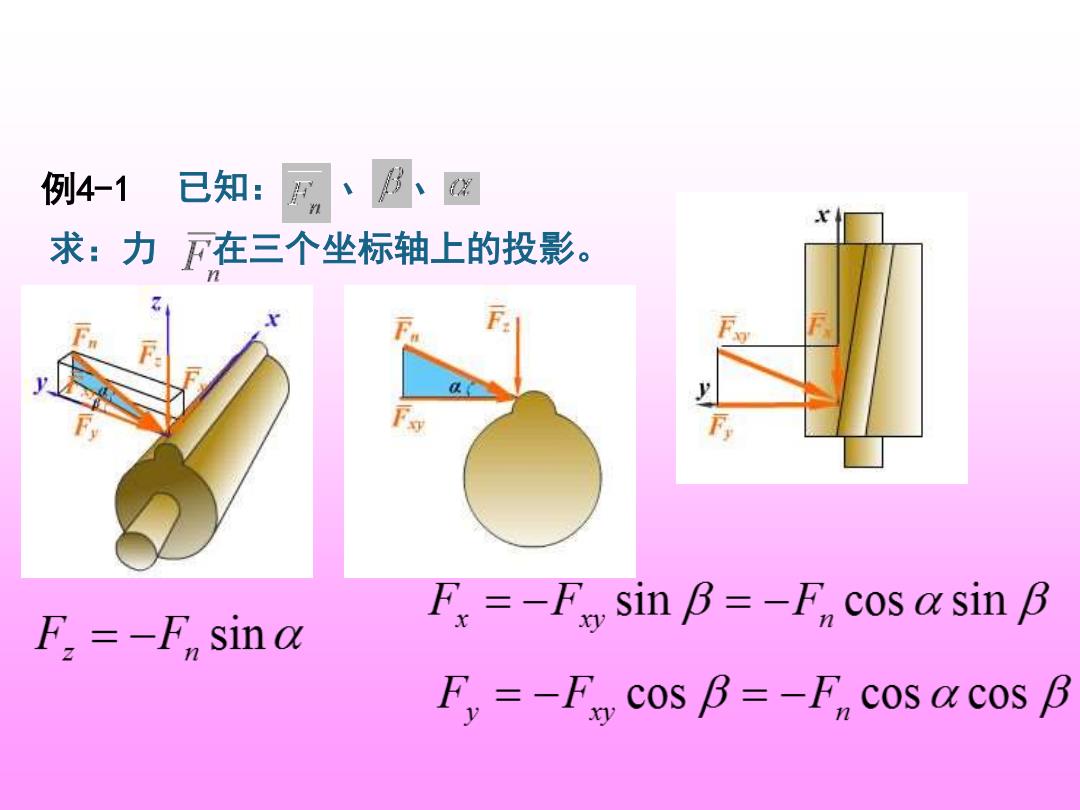
例4-1已知: B、 求:力F在三个坐标轴上的投影。 F: F.=-F sin a F=-F sin B=-F cos a sin B Fy=-F Cos B=-F cos a cos B
例4-1 已知: 、 、 求:力 在三个坐标轴上的投影