
2.集合之间的关系及运算 定义2.设有集合A,B,若x∈A必有x∈B,则称A 是B的子集,或称B包含A,记作AB. 若AcB且BCA,则称A与B相等,记作A=B. 例如,NCZ,ZCQ,QCR 显然有下列关系: (1)ACA;A=A4;CA (2)ACB且BcC>ACC Oao⊙⊙8
是 B 的子集 , 或称 B 包含 A , 2. 集合之间的关系及运算 定义2 . 则称 A A B. 若 且 则称 A 与 B 相等, A = B . 例如 , 显然有下列关系 : , , 设有集合 A,B, 若 x A x B, 记作 记作 必有 机动 目录 上页 下页 返回 结束

定义3.给定两个集合A,B,定义下列运算 并集AUB={xx∈A或x∈B} AUB 交集A∩B={xx∈A且x∈B} AB 差集A八B={xx∈A且xEB} A∩B 余集B=A\B(其中BCA) 直积A×B={(x,y)x∈A,y∈B} 特例: RXR记R2 B AxB 为平面上的全体点集 OOo⊙⊙8
A c BA B 定义 3 . 给定两个集合 A, B, 并集 A B = x 交集 A B = x 且 差集 A \ B = x 且 x B 定义下列运算: A B A B 余集 B A\ B ( B A) c A = 其中 直积 A B = (x, y) x A , y B 特例: RR 记 2 R 为平面上的全体点集 A A\ B B A B A B 机动 目录 上页 下页 返回 结束 或
二、 映射 1.映射的概念 引例1. 某校学生的集合 学号的集合 按一定规则查号 某教室座位 某班学生的集合 的集合 按一定规则入座 oo0oo
二、 映射 1. 映射的概念 某校学生的集合 学号的集合 按一定规则查号 某班学生的集合 某教室座位 的集合 按一定规则入座 机动 目录 上页 下页 返回 结束 引例1
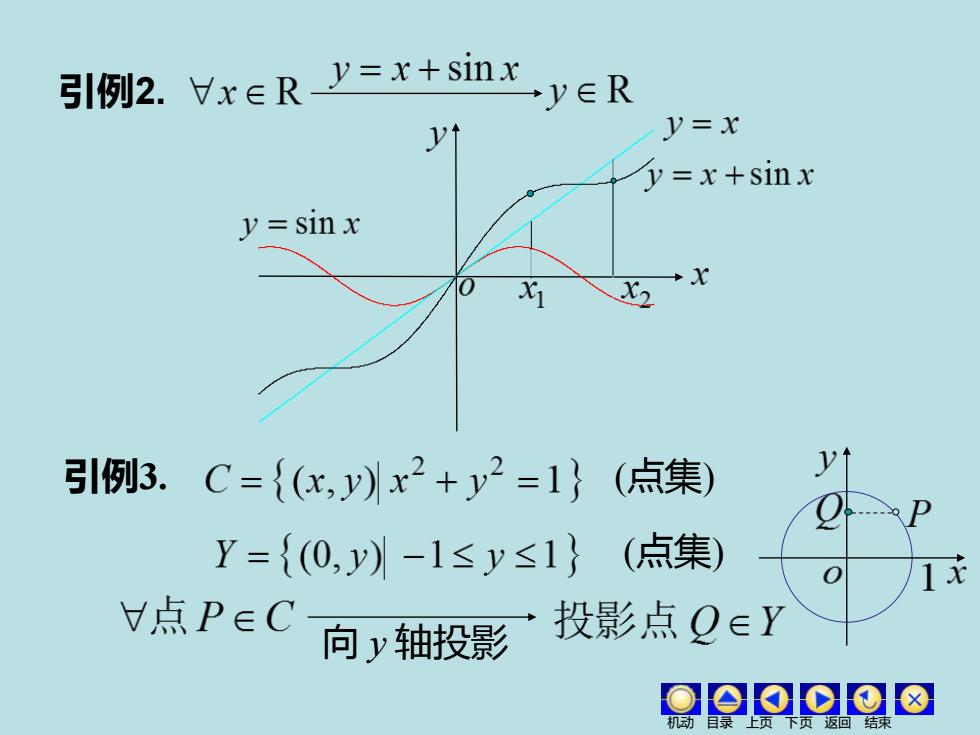
引例2.Vx∈Ry=x+sinxy∈R y=x V=x+sinx y=sin x x 引例3.C={(x,y)x2+y2=1}(点集) Y={(0,y)-1≤y≤1}(点集) V点PeC 向y轴投影 投影点QeY o0o0 机
引例2. 引例3. (点集) (点集) 向 y 轴投影 机动 目录 上页 下页 返回 结束

定义4.设X,Y是两个非空集合,若存在一个对应规 则f,使得Vx∈X,有唯一确定的yeY与之对应,则 称f为从X到Y的映射,记作f:X→Y. 元素y称为元素x在映射f下的像,记作y=f(x) 元素x称为元素y在映射f下的原像. 集合X称为映射f的定义域; Y的子集f(X)={f(x)x∈X}称为f的值域 注意:1)映射的三要素一定义域,对应规侧,值域 2)元素x的像y是唯一的,但y的原像不一定唯一 gao⊙回⑧
定义4. 设 X , Y 是两个非空集合, 若存在一个对应规 则 f , 使得 有唯一确定的 与之对应 , 则 称 f 为从 X 到 Y 的映射, 记作 f : X →Y. 元素 y 称为元素 x 在映射 f 下的 像 , 记作 y = f (x). 元素 x 称为元素 y 在映射 f 下的 原像 . 集合 X 称为映射 f 的定义域 ; Y 的子集 f (X) = f (x) x X 称为 f 的 值域 . 注意: 1) 映射的三要素— 定义域 , 对应规则 , 值域 . 2) 元素 x 的像 y 是唯一的, 但 y 的原像不一定唯一 . X f Y 机动 目录 上页 下页 返回 结束