
最大似然估计量 定义最大似然估计量0为使得L()最大的值。通过解下列方程 aL(0) =0 i=1,.,m a0, 通常可以找到对于m个参数的解6,,n。 有时候L(0)可以有好几个极大值 取最大值 注意,1)该方法利用了所有信息,与如何划分数据分布区间无关: 2)定义的最大似然估计量并不保证它们总是最优的。 需要对诸如无偏性,有效性等问题进行研究 多数情况下对于足够大样本,最大似然法的确能给出了期待的好结果。 即使是小样本的情况,虽然并不总是达到最优,但它通常仍然能给出最 好的实用解。 6
6 最大似然估计量 取最大值 取最大值 ˆ 定义最大似然估计量θ θ 为使得 L ( ) 最大的 θ值。通过解下列方程 1 ˆ ˆ ,..., 通常可以找到对于 m 个参数的解 θ θ m 。 i m L i 0 1,..., ( ) = = ∂ ∂ θ θ 有时候 L ( θ ) 可以有好几个极大值 注意, 1)该方法利用了所有信息,与如何划分数据分布区间无关; 2)定义的最大似然估计量并不保证它们总是最优的。 需要对诸如无偏性,有效性等问题进行研究 多数情况下对于足够大样本,最大似然法的确能给出了期待的好结果。 即使是小样本的情况,虽然并不总是达到最优,但它通常仍然能给出最 好的实用解
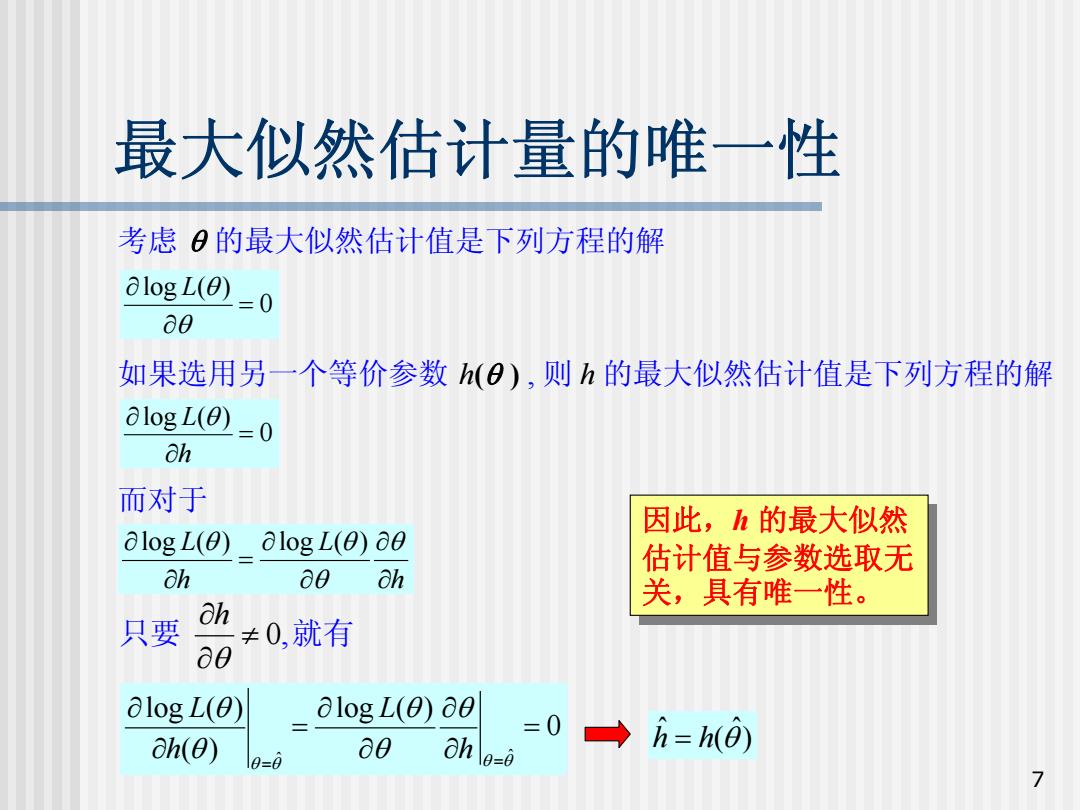
最大似然估计量的唯一性 考虑0的最大似然估计值是下列方程的解 olog L(0) =0 a0 如果选用另一个等价参数h(8),则h的最大似然估计值是下列方程的解 alog L(0) =0 8h 而对于 因此,h的最大似然 olog L(0) alog L(0)80 估计值与参数选取无 Oh a0 8h 关,具有唯一性。 Oh 只要 ≠0,就有 a0 alog L(0) alogL(0)80 =0 ah(0) 0=0 a0 Oh →h=h(⊙) = 7
7 最大似然估计量的唯一性 考虑 θ 的最大似然估计值是下列方程的解 lo g ( ) 0 L θ θ ∂ = ∂ 如果选用另一个等价参数 h ( θ ) , 则 h 的最大似然估计值是下列方程的解 lo g ( ) 0 L h ∂ θ = ∂ 而对于 lo g L L ( ) lo g ( ) h h θ θ θ θ ∂ ∂ ∂ = ∂ ∂ ∂ , 0 h θ ∂ ≠ ∂ 只要 就有 ˆ ˆ lo g ( ) lo g ( ) 0 ( ) L L h h θ θ θ θ θ θ θ θ θ = = ∂ ∂ ∂ = = ∂ ∂ ∂ ˆ ˆ h h = ( ) θ 因此, h 的最大似然 估计值与参数选取无 关,具有唯一性。 因此, h 的最大似然 估计值与参数选取无 关,具有唯一性

最大似然估计量的渐进性 如果元=(x,,xn)是分布f(x;O)的随机样本,0是参数0的最大似然 估计。则当样本容量→0时,0的分布趋近于一个正态分布,即 f(d:0)=(d,0,VL0]) 其中方差 [=- a2log f(x;0) a20 在推断大样本的最大似然估计的误差时,可以利用 测量误差理论中最常见的正态分布进行推断。 注意:样本容量多大,才能近似利用极限正态分布,才可以看作最 有效的估计,这将依赖于观测量的概率密度函数的具体形式。但对 于指数型分布会有一些最优性质
8 最大似然估计量的渐进性 1 ˆ ( ,..., ) ( ; ) ˆ n x x x f x n θ θ θ θ = → ∞ G 如果 是分布 的随机样本, 是参数 的最大似然 估计。则当样本容量 时, 的分布趋近于一个正态分布,即 ˆ ˆ f N ( ; θ θ θ ) = ( ;θ,V [ θ ] ) 其中方差 1 1 2 2 2 2 lo g ( ) 1 lo g ( ; ) [ ] L f x V n θ θ θ θ θ − − ⎛ ⎞ ∂ ∂⎛ ⎞ = −⎜ ⎟ = − ⎜ ⎟ ⎜ ⎟ ∂ ∂ ⎜ ⎟ ⎝ ⎠ ⎝ ⎠ 在推断大样本的最大似然估计的误差时,可以利用 测量误差理论中最常见的正态分布进行推断。 注意:样本容量多大,才能近似利用极限正态分布,才可以看作最 有效的估计,这将依赖于观测量的概率密度函数的具体形式。但对 于指数型分布会有一些最优性质。 注意:样本容量多大,才能近似利用极限正态分布,才可以看作最 有效的估计,这将依赖于观测量的概率密度函数的具体形式。但对 于指数型分布会有一些最优性质

例子:指数概率密度函数参数 考虑指数概率密度函数 f(t;t)=Le-u T 并假设有一数据样本t1,.,tn。通常为了方便起见,可采用对数形式(对同 样的参数值,该定义并不会改变最大值的位置) eue)立oeu,-2oeg 例子:用蒙特卡罗 0.75 方法产生具有仁1 的50个t值,得到 令logL-0,并求解, 0.5 t=1.062 0.25 是平均寿命的 n 最大似然估计 0 i=1 5
9 例子:指数概率密度函数参数 考虑指数概率密度函数 τ τ τ 1 / ( ; ) t f t e− = 并假设有一数据样本 t1,…,tn。通常为了方便起见,可采用对数形式(对同 样的参数值,该定义并不会改变最大值的位置)。 1 1 1 log ( ) log ( ; ) log n n i i i i t L f τ τ t = = τ τ ⎛ ⎞ = = − ⎜ ⎟ ⎝ ⎠ ∑ ∑ log 0 L τ τ ∂ = ∂ 令 ,并求解 , ∑ = = n i i t n 1 1 τ ˆ 例子:用蒙特卡罗 方法产生具有τ=1 的50个 t 值,得到 τ ˆ =1.062 是平均寿命的 最大似然估计