
教案第十三章电磁感应、电磁场 第十三章 电磁感应、电磁场Electromagnetic Induction, Electromagnetic Field §1电磁感应定律Law of Electromagnetic Induction 阐述电磁感应现象,1820年,丹麦物理学家奥斯特发现电流的磁效应,揭示了电现 象与磁现象有关的事实,展示了由电可以生磁一—在导线中通以稳恒电流,则在其周围 的空间产生稳恒的磁场,由此,人们开始从磁生电的角度去探索。1825年,瑞士物理学 家科拉顿用灵敏电流计检查磁铁插入螺线管中是否有电流产生,为了排除磁铁对电流计 的影响,他把电流计和螺线管分别放在两个实验中。在螺线管中放入(抽出)磁铁后, 再到另一个房间观察电流计指针是否发生偏转,结果总是得到零的结果,为什么? 1.电磁感应定律 法拉弟经过一系列实验,于1831年正式提出电磁感应定律:当穿过闭合回路所围面 积的磁通量发生变化时,不论这种变化是什么原因引起的,回路中都会建立起感应电动 势,因此感应电动势正比于磁通量对时间变化率 的负值,即 国际单位制中k取1。 根据感应定律,可判断下图中感应电流方向 如图中所示。 在应用电磁感应定律时,一定要弄清楚回路绕行 方向与感应电动势方向之间的关系,下图为各种情况下感应电动势的方向。 中为回路所围面积的磁通量,若回路由N匝密绕线圈组成,若每匝线圈的磁通量为, 则穿过N匝线圈的磁通量为yw=N,y为磁通量匝数,也叫磁链。 若回路的电阻为R,则回路中的感 1"/ 应电流为: (2) d-0.(ddihj-0.Er0 0.(do)<o.E>0 g=可h=员o=京a-o) 206 E k0,(dhth)<0,E>0 c0,(ddh>0,E<0
教案 第十三章 电磁感应、电磁场 206 第十三章 电磁感应、电磁场 Electromagnetic Induction, Electromagnetic Field §1 电磁感应定律 Law of Electromagnetic Induction 阐述电磁感应现象,1820 年,丹麦物理学家奥斯特发现电流的磁效应,揭示了电现 象与磁现象有关的事实,展示了由电可以生磁——在导线中通以稳恒电流,则在其周围 的空间产生稳恒的磁场,由此,人们开始从磁生电的角度去探索。1825 年,瑞士物理学 家科拉顿用灵敏电流计检查磁铁插入螺线管中是否有电流产生,为了排除磁铁对电流计 的影响,他把电流计和螺线管分别放在两个实验中。在螺线管中放入(抽出)磁铁后, 再到另一个房间观察电流计指针是否发生偏转,结果总是得到零的结果,为什么? 1.电磁感应定律 法拉弟经过一系列实验,于 1831 年正式提出电磁感应定律:当穿过闭合回路所围面 积的磁通量发生变化时,不论这种变化是什么原因引起的,回路中都会建立起感应电动 势,因此感应电动势正比于磁通量对时间变化率 的负值,即 dt d E k i = − 国际单位制中 k 取 1。 根据感应定律,可判断下图中感应电流方向 如图中所示。 在应用电磁感应定律时,一定要弄清楚回路绕行 方向与感应电动势方向之间的关系,下图为各种情况下感应电动势的方向。 为回路所围面积的磁通量,若回路由 N 匝密绕线圈组成,若每匝线圈的磁通量为, 则穿过 N 匝线圈的磁通量为=N,为磁通量匝数,也叫磁链。 若回路的电阻为 R,则回路中的感 应电流为: dt d R R E I i i 1 = = − (2) dt dq I = ( ) 1 1 1 2 2 1 = = − = − R d R q Idt v B Ii n n n n Ei Ei Ei Ei (ddt)>0, Ei<0 (ddt)<0, Ei>0 (ddt)<0, Ei>0 (ddt)>0, Ei<0

教案第十三章电磁感应、电磁场 可计算出穿过回路的电荷,如果测出流过回路的电荷q,就可以知道磁通量的变化, 这就是磁强计的原理,可用磁强计来探测磁场的变化,这在地质勘探和地震监测中有者 广泛的应用。 2.楞次定律 演示实验(楞次定律)、分析实验 中现象,即下列情况: 左图中:中=「B>0:而 d地0 由6=出知:5<0与日路方 向相反,此时,感应电流所产生的B与 B,反向,它阻碍磁铁的运动。 争=民店>0:出<0:=出>0,此时,感应电流产生的酸场与瓦同向, 它亦阻碍磁铁远离线圈。 上述结论是符合能量守恒定律的,因为感应电动势阻碍磁铁的运动,因此,若想移 动磁铁,外力需作功,若不是这样,那么稍微移动一下磁铁,那它将运动的越来越快, 违反能量守恒3。因此,法拉第电磁感应定律中的负号体现了能量守恒定律,愣次定律 (Lenz'slaw)。 闭合回路中感应电流的方向,总是企图使感应电流本身所产生的通过回路面积的磁 通量,去补偿或者说是反抗相起感应电流的磁通量的改变。 §2动生电动势和感生电动势Motional Electromotive Force and Induced Electromotive Force 1.动生电动势: 由导体在磁场中移动而产生的感应电动劝 势为动生电动势。 =B-N,可判知其方向如图 图中:,-a
教案 第十三章 电磁感应、电磁场 207 可计算出穿过回路的电荷,如果测出流过回路的电荷 q,就可以知道磁通量的变化, 这就是磁强计的原理,可用磁强计来探测磁场的变化,这在地质勘探和地震监测中有着 广泛的应用。 2.楞次定律 演示实验(楞次定律)、分析实验 中现象,即下列情况: 左图中: = 0 0 B ds ; 而 0 dt d 由 dt d Ei = − 知: Ei 0 与回路方 向相反,此时,感应电流所产生的 B 与 B0 反向,它阻碍磁铁的运动。 = 0 0 B ds ; 0 dt d ; = − 0 dt d Ei ,此时,感应电流产生的磁场与 B0 同向, 它亦阻碍磁铁远离线圈。 上述结论是符合能量守恒定律的,因为感应电动势阻碍磁铁的运动,因此,若想移 动磁铁,外力需作功,若不是这样,那么稍微移动一下磁铁,那它将运动的越来越快, 违反能量守恒 3。因此,法拉第电磁感应定律中的负号体现了能量守恒定律,愣次定律 (Lenz’s law)。 闭合回路中感应电流的方向,总是企图使感应电流本身所产生的通过回路面积的磁 通量,去补偿或者说是反抗相起感应电流的磁通量的改变。 §2 动生电动势和感生电动势 Motional Electromotive Force and Induced Electromotive Force 1.动生电动势: 由导体在磁场中移动而产生的感应电动劝 势为动生电动势。 图中: B lv dt d Ei = = ,可判知其方向如图 v B Ii a b dS l n B0 N B0 N Ei Ei

教案第十三章电磁感应、电磁场 所示(:安>0,而00,>0》 下面看b移动时,内部电子所受的洛沦兹力: F=(-e)p×B=(-e)Ek:E=下×B看为等效电场。 定义:E,=事E,·d:E,等于将单位正电荷电电源内部从负相移到正极非都电力作的 功。 E在ab外的导体上为0,有:E=fEdi=E4d 上式还可写为:E,=[(下×B)dd 推广:(1)式可以用来计算在一般情况下,导体在磁场中运动时产生的感应电动势 例:如图,已知,铜棒的角速度@,长为L,和外场B,求E 解:E,为:(di由0a) E=(xB)-di=-[Bdl=-[loBdl=-BoL a点电势高,电流由a→0与d方向相反。 2 2 2 0=-21 (回路方向选0-a,B5=B号0) + 2.感生电动势 导体不动,磁场发生变化而产生的感应电动势。 变化的磁场要在其周围激发电场,即感应电场E4,感应电场的电力线是闭合的,感应电 场在任意闭合回路产生的电动势为: 6==路盟s2 这是由Maxwell总结出的。 (2)式适用于任何闭合回路,不管此闭合回路是由导体构成,回路有感应电流或是 不是由导体构成的,无电流,但感应电动势总是存在的。 例感:把电号率为的园智生收入磁块B中,受上为 常数,求盘内的感应电流值。 208
教案 第十三章 电磁感应、电磁场 208 所示(∵ 0 dt d ,而<0,Ei 0 ) 下面看 ab 移动时,内部电子所受的洛沦兹力: Ek F e v B e = (− ) = (− ) ; Ek v B = 看为等效电场。 定义: E = E dl i k ;Ei 等于将单位正电荷电电源内部从负相移到正极非都电力作的 功。 ∵ Ek 在 ab 外的导体上为 0,有: E E dl E dl b a i k k = = 上式还可写为: E v B dl b a i = ( ) 推广:(1)式可以用来计算在一般情况下,导体在磁场中运动时产生的感应电动势。 例:如图,已知,铜棒的角速度,长为 L,和外场 B ,求 Ei。 解:Ei 为:( dl 由 0→a) 2 0 0 0 2 1 E (v B) dl vBdl l Bdl B L L L L i = = − = − = − ; a 点电势高,电流由 a→0 与 dl 方向相反。 另解: 2 2 2 2 1 2 2 B L L B L B dt d dt d Ei = − = − = − = − (回路方向选 0→a, 2 2 L Bs = B ) 2.感生电动势 导体不动,磁场发生变化而产生的感应电动势。 变化的磁场要在其周围激发电场,即感应电场 Ek ,感应电场的电力线是闭合的,感应电 场在任意闭合回路产生的电动势为: ds dt dB dt d E E dl s i k = = − = − (2) 这是由 Maxwell 总结出的。 (2)式适用于任何闭合回路,不管此闭合回路是由导体构成,回路有感应电流或是 不是由导体构成的,,无电流,但感应电动势总是存在的。 例题:把电导率为的圆铝盘放入磁块 B 中, k dt dB = 为一 常数,求盘内的感应电流值。 b L O B R r dr h B
教案第十三章电磁感应、电碰场 解:盘中取一半径r,宽为d,高为h的圆环,在此圆环中 6=f我i=-盟 即:E=k知2 此圆环的电阻R= 则山=员空 1-山-t-Rh 3.电子感应加速器 电子感应加速器是利用变化的磁场激发的电场来加速电子的。 如图,真空放在频率为几十赫的交变磁铁中间,电子沿回路方向被注入真空室之后,在 感生电场作用下被加速,与此同时,电子还受到磁场对它的洛仑兹力作用,从而沿着环 形室内的圆形轨道运动。 环形真空简 环形真空管 子轨 电子感应加速器中的几个问题 1加速时间 由图可知,电子 B 只有在第一和第四 个}周期被加速,另 外,为使电子不断被 加速,应使电子沿园 形轨道运动。电子受 涡旋电场方向 磁场的洛仑兹力应
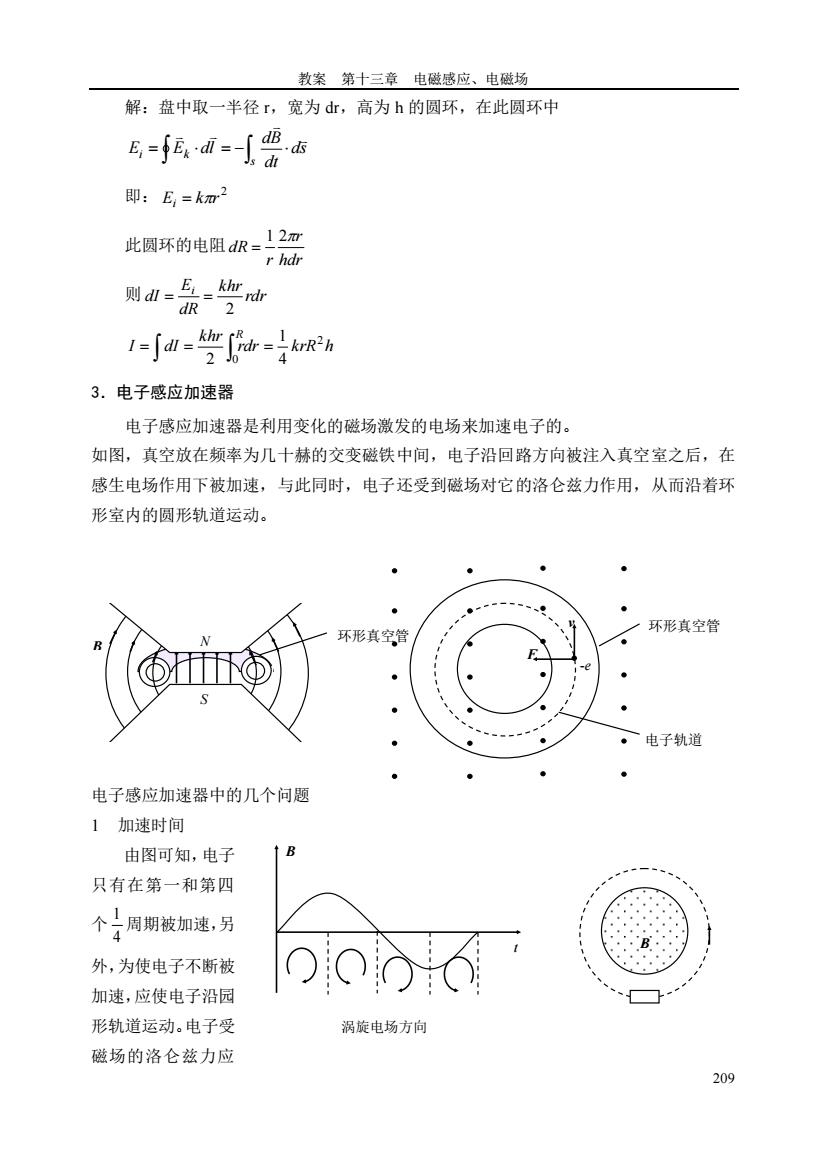
教案 第十三章 电磁感应、电磁场 209 解:盘中取一半径 r,宽为 dr,高为 h 的圆环,在此圆环中 ds dt dB E E dl s i k = = − 即: 2 E k r i = 此圆环的电阻 hdr r r dR 1 2 = 则 rdr khr dR E dI i 2 = = rdr krR h khr I dI R 2 0 4 1 2 = = = 3.电子感应加速器 电子感应加速器是利用变化的磁场激发的电场来加速电子的。 如图,真空放在频率为几十赫的交变磁铁中间,电子沿回路方向被注入真空室之后,在 感生电场作用下被加速,与此同时,电子还受到磁场对它的洛仑兹力作用,从而沿着环 形室内的圆形轨道运动。 电子感应加速器中的几个问题 1 加速时间 由图可知,电子 只有在第一和第四 个 4 1 周期被加速,另 外,为使电子不断被 加速,应使电子沿园 形轨道运动。电子受 磁场的洛仑兹力应 N 环形真空管 S B 电子轨道 v 环形真空管 F -e B 涡旋电场方向 t B B

教案第十三章电磁感应、电磁场 指向园心。考虑如上两个因素,只有在第一个周期内电子被加速,(第四个}周期洛仑 兹力沿径向向外)。因此,在加速器中,在每个第一上周期末,利用特殊装置将电子束引 离轨道射在靶上,因E非常大,即使在如此短的时间内,电子的动能还能达到几个个 Mel以上。 2磁场的设计 RR=m 因为emB= B 由此式知,若要使R保持不变,B须与V之比为一常数。 因为:写=成”由第三定律得: d认m=2成w 设开始时-0,v0,积分得 得:R=四与前式比较得: 8五 即:轨道上的磁感应强度值等于轨道内磁感应强度的平均值的一半,此时,电子能 在稳定的轨道上被加速。 4.涡电流 当大块导体处在变化的磁场中时, 导体中会产生感应电流,这种在大块导 金属积 体中流动的感应电流,称为涡电流,由 于大块导体的电阻很小,涡电流可以达 到很大的强度,产生很强的热效应,故 在工业上常用2频感应炉来熔化金属, 这种加热法的优点是金属内部各处均匀 加热,且可不被氧化。 涡电流的产生 工频感应炉示意图 210
教案 第十三章 电磁感应、电磁场 210 指向园心。考虑如上两个因素,只有在第一个 4 1 周期内电子被加速,(第四个 4 1 周期洛仑 兹力沿径向向外)。因此,在加速器中,在每个第一 4 1 周期末,利用特殊装置将电子束引 离轨道射在靶上,因 Et 非常大,即使在如此短的时间内,电子的动能还能达到几个个 Mel 以上。 2 磁场的设计 因为 eB mv R R mv evB = = 2 由此式知,若要使 R 保持不变,B 须与 v 之比为一常数。 因为: dt d R Et = − 2 1 ;由第二定律得: dt d R e eE dt d mv t = − = 2 ( ) = d R e d mv 2 ( ) 设开始时=0,v=0,积分得: R B R e R e mv 2 2 2 = = 得: eB mv R 2 = 与前式比较得: B B 2 1 = 即:轨道上的磁感应强度值等于轨道内磁感应强度的平均值的一半,此时,电子能 在稳定的轨道上被加速。 4.涡电流 当大块导体处在变化的磁场中时, 导体中会产生感应电流,这种在大块导 体中流动的感应电流,称为涡电流,由 于大块导体的电阻很小,涡电流可以达 到很大的强度,产生很强的热效应,故 在工业上常用 2 频感应炉来熔化金属, 这种加热法的优点是金属内部各处均匀 加热,且可不被氧化。 金属快 B 涡电流的产生 工频感应炉示意图