
教案第十五章机械波 第十五章机械波Mechanical Wave 在上一章讨论振动的基础上,本章将进一步研究振动在空间的传播过程一波动。波动 分为机械波和电磁波。机械振动在弹性介质中的传播形成机械波:交变电磁场在空间的传 播形成电磁波。机械波和电磁波在本质上是不相同的,但是它们都具有波动的共同特征, 即都具有一定的传播速度,且都伴随着能量的传播,都能产生反射、折射、干涉和衍射等 现象,而且有相似的数学表达形式。 一 基本要求 1熟练掌握平面简谐波的波函数,并深刻理解描述波动的各物理量的物理意义,能 根据给定的条件求出波函数: 2理解惠更斯原理和波的叠加原理,熟练掌握波的干涉原理和干涉加强,减弱条件: 3 掌握驻波的形成和特点,建立半波损失的概念 4理解多普勒效应及其公式,并能求解一些具体问题。 二基本内容 1波动的基本概念 1)机械波:形成机械波必须有波源(振动物体)和弹性介质。 2)横波和纵波:质点的振动方向与波的传播方向相互垂直的波叫做横波:两者相互平行的 波叫做纵波。横波和纵波是波动的两种基本类型,各种复杂的波都可以分解成横波与纵波, 并分别处理。 3)波线与波面:为描述形象起见,自波源沿各传播方向画一些带箭头的线,叫做波线。介 质中振动的相位相同的各点组成的面叫做同相面或波面。在某一时刻,最前面的波面叫做 波前。 4)平面波和球面波:波面为平面的波称为平面波:点波源的波面是球面,叫做球面波。在 离波源足够远处,且观察范围不大时,球面波可按平面波处理。 5)波速(相速):振动状态(即相位)在空间的传播速度称为波速或相速。它与波动的 特性无关,仅取决于传播介质的性质。 6)波长1:同一波线上相位差为2π的两相邻质点之间的距离,即一个完整波形的长度。它 反映波在空间上的周期性。 )波的周期T:一个完整波形通过波线上某点所需的时间。它反映波在时间上的周期性。 波的周期与传播介质各质点的振动周期相同。 8)波的频率单位时间通过波线上某点的完整波形的数目,它与介质质元的振动频率相 等。 239
教案 第十五章 机械波 239 第十五章 机械波 Mechanical Wave 在上一章讨论振动的基础上,本章将进一步研究振动在空间的传播过程-波动。波动 分为机械波和电磁波。机械振动在弹性介质中的传播形成机械波;交变电磁场在空间的传 播形成电磁波。机械波和电磁波在本质上是不相同的,但是它们都具有波动的共同特征, 即都具有一定的传播速度,且都伴随着能量的传播,都能产生反射、折射、干涉和衍射等 现象,而且有相似的数学表达形式。 一 基本要求 1 熟练掌握平面简谐波的波函数,并深刻理解描述波动的各物理量的物理意义,能 根据给定的条件求出波函数; 2 理解惠更斯原理和波的叠加原理,熟练掌握波的干涉原理和干涉加强,减弱条件; 3 掌握驻波的形成和特点,建立半波损失的概念 4 理解多普勒效应及其公式,并能求解一些具体问题。 二 基本内容 1 波动的基本概念 1) 机械波:形成机械波必须有波源(振动物体)和弹性介质。 2) 横波和纵波:质点的振动方向与波的传播方向相互垂直的波叫做横波;两者相互平行的 波叫做纵波。横波和纵波是波动的两种基本类型,各种复杂的波都可以分解成横波与纵波, 并分别处理。 3) 波线与波面:为描述形象起见,自波源沿各传播方向画一些带箭头的线,叫做波线。介 质中振动的相位相同的各点组成的面叫做同相面或波面。在某一时刻,最前面的波面叫做 波前。 4) 平面波和球面波:波面为平面的波称为平面波;点波源的波面是球面,叫做球面波。在 离波源足够远处,且观察范围不大时,球面波可按平面波处理。 5) 波速(相速)u:振动状态(即相位)在空间的传播速度称为波速或相速。它与波动的 特性无关,仅取决于传播介质的性质。 6) 波长:同一波线上相位差为 2的两相邻质点之间的距离,即一个完整波形的长度。它 反映波在空间上的周期性。 7) 波的周期 T:一个完整波形通过波线上某点所需的时间。它反映波在时间上的周期性。 波的周期与传播介质各质点的振动周期相同。 8) 波的频率:单位时间通过波线上某点的完整波形的数目,它与介质质元的振动频率相 等

教案第十五章机械波 9)波数k:它的数值等于在2π长度内所包含的完整波的个数。 10)波速、波长、周期、频率、波数之间的关系: =子=水k=2织-e 2简谐波 1)简谐波:波源和介质质点都作简谐振动的波称为简谐波。各种复杂的波形都可看成由许 多不同频率的简谐波的叠加。 2)平面简谐波的波函数:在无吸收的均匀介质中沿X轴传播的平面简谐波的波函数为 y=4 cs于2+p =4 eos(宁+克+j =Acos[@年2x5+p 其中:“-”表示波沿X轴正方向传播:“+”表示波沿X轴负方向传播。 3)波函数的物理意义:波函数是x和1的函数。给定x,表示x处质点的振动,即给出x 处质点任意时刻离开自己平衡位置的位移:给定,表示1时刻的波形,即给出1时刻质点 离开自己平衡位置的位移。 3波传播的能量 )能量密度:单位体积介质的波动能量。 y=( 在一个周期内的平均值叫做平均能量密度,万=0。 2)平均能流密度:单位时间通过垂直于传播方向的单位面积的平均能流1=一Pm'Au, 能流密度是矢量,方向与波数方向相同,它的大小表示波的强度。在均匀各向同性介 质中,平面波的强度不变,球面波的强度与半径的平方成反比 3)波动方程 在无吸收的均匀介质中,一切平面波都遵守微分方程: 在三维空间中传播的一切波动过程都遵守微分方程: 器++ 4惠更斯原理 240
教案 第十五章 机械波 240 9) 波数 k:它的数值等于在 2长度内所包含的完整波的个数。 10) 波速、波长、周期、频率、波数之间的关系: u k T u = = = = 2 , 2 简谐波 1) 简谐波:波源和介质质点都作简谐振动的波称为简谐波。各种复杂的波形都可看成由许 多不同频率的简谐波的叠加。 2) 平面简谐波的波函数:在无吸收的均匀介质中沿 X 轴传播的平面简谐波的波函数为 cos[( 2 ) ] cos[2 ( ) ] cos[ ( ) ] = + = + = + x A t x T t A u x y A t 其中:“−”表示波沿 X 轴正方向传播;“+”表示波沿 X 轴负方向传播。 3) 波函数的物理意义:波函数是 x 和 t 的函数。给定 x,表示 x 处质点的振动,即给出 x 处质点任意时刻离开自己平衡位置的位移;给定 t,表示 t 时刻的波形,即给出 t 时刻质点 离开自己平衡位置的位移。 3 波传播的能量 1) 能量密度:单位体积介质的波动能量。 sin ( ) 2 2 2 u x y = A t − 在一个周期内的平均值叫做平均能量密度, 2 2 2 1 = A 。 2) 平均能流密度:单位时间通过垂直于传播方向的单位面积的平均能流 I A u 2 2 2 1 = , 能流密度是矢量,方向与波数方向相同,它的大小表示波的强度。在均匀各向同性介 质中,平面波的强度不变,球面波的强度与半径的平方成反比。 3) 波动方程 在无吸收的均匀介质中,一切平面波都遵守微分方程: 2 2 2 2 2 1 t y x u y = 在三维空间中传播的一切波动过程都遵守微分方程: 2 2 2 2 2 2 2 2 2 1 x y z u t = + + 4 惠更斯原理

教案第十五章机械波 介质中波阵面上各点都可看做子波波源,任一时刻这些子波的包迹就是新的波阵面 5波的叠加原理 几列波可以保持各自的特点通过同一介质,好像没有其他波一样:在它们相重叠的区 域内,每一点的振动都是各个波单独在该点产生的振动的矢量和。 6波的干涉 )波的干涉现象:由频率相同、振动方向相同、相位相同或相位差恒定的两个波源所发 出的波,在空间相遇,出现某些点振动始终加强,某些点振动始终减弱或完全抵消的 现象称为波的干涉现象。能产生干涉现象的波叫做相关波,相应的波源叫做相干波源。 2)波的相干条件:频率相同、振动方向不相互垂直、相位相同或相位差恒定。 3)干涉加强和减弱的条件:两相关波源发出的波在空间某处相遇叠加时,干涉加强或减 弱的条件由两波在该处的相位差: 40=--受6-)决定. 4p=±2k+r k=0,1,2,…,振幅最大,A=A+A k=01,2,…,振幅最小,A=4-4 当两相关波源的振动的相位相同时,干涉条件也可用波程差表示: 4=A+A 6=5--±(2k+ A=4-A4 k=012… 7驻波 两列振幅相同的相关波,在同一直线上沿相反方向传播时,形成驻波。它实际上是稳 定的分段振动。在波节和波腹。相邻两波节或波幅之间的距离为22。波节两边的介质,振 动的相位差为π。 8多普勒相应 当波源S与观察者R之间有相对运动时,观察者所接收到的波颊率?与波源所发射的 波的频率s不同,这种现象称为多普勒相应。 波源与观察者在同一直线上运动时,二者关系为 上面一组符号表示相互靠近:下面一组符号相互远离。 241
教案 第十五章 机械波 241 介质中波阵面上各点都可看做子波波源,任一时刻这些子波的包迹就是新的波阵面。 5 波的叠加原理 几列波可以保持各自的特点通过同一介质,好像没有其他波一样;在它们相重叠的区 域内,每一点的振动都是各个波单独在该点产生的振动的矢量和。 6 波的干涉 1) 波的干涉现象:由频率相同、振动方向相同、相位相同或相位差恒定的两个波源所发 出的波,在空间相遇,出现某些点振动始终加强,某些点振动始终减弱或完全抵消的 现象称为波的干涉现象。能产生干涉现象的波叫做相关波,相应的波源叫做相干波源。 2) 波的相干条件:频率相同、振动方向不相互垂直、相位相同或相位差恒定。 3) 干涉加强和减弱的条件:两相关波源发出的波在空间某处相遇叠加时,干涉加强或减 弱的条件由两波在该处的相位差: ( ) 2 2 1 2 1 = − − r − r 决定。 1 2 1 2 0,1,2, , 0,1,2, , (2 1) 2 k A A A k A A A k k = = − = = + + = 振幅最小, 振幅最大, 当两相关波源的振动的相位相同时,干涉条件也可用波程差表示: 0,1,2, 2 (2 1) 1 2 1 2 2 1 = = − = + + = − = k A A A A A A k k r r 7 驻波 两列振幅相同的相关波,在同一直线上沿相反方向传播时,形成驻波。它实际上是稳 定的分段振动。在波节和波腹。相邻两波节或波幅之间的距离为/2。波节两边的介质,振 动的相位差为。 8 多普勒相应 当波源 S 与观察者 R 之间有相对运动时,观察者所接收到的波频率R 与波源所发射的 波的频率S 不同,这种现象称为多普勒相应。 波源与观察者在同一直线上运动时,二者关系为 S S R R u v u v = 上面一组符号表示相互靠近;下面一组符号相互远离

教案第十五章机械波 S1机械波的几个概念Some Concepts of Mechanical Wave 一机械波的形成 机械振动在弹性介质(固体、液体和气体)内传播就形成机械波,这是因为弹性介质 内各质点之间有弹性力相互作用着。当介质中某一质点离开平衡位置时,这就发生了相变, 于是,一方面邻近质点将对它施加弹性回复力,使它回到平衡位置,并在平衡位置附近振 动起来:另一方面根据牛顿第三定律,这个质点也将对邻近质点施加弹性力,迫使邻近质 点也在自己的平衡位置附近振动起来。这样,当弹性介质中的一部分发生振动时,由于各 部分之间的弹性相互作用,振动就由近及远地传播开去,形成了振动。 弹性介质:组成介质的质点或质元之间以弹性力相互作用着,当介质中某一质点P偏 离平衡位置时,由于形变相邻质点就将对它施以弹性力作用,使它回到平衡位置。但由于 惯性的存在,P质点回到平衡位置后,又将向相反方向偏离。于是质点P就在平衡位置附件 振动起来。与此同时质点P也对其相邻质点施以弹性力作用,使相邻质点也在其平衡位置 附近振动,·,就这样振动就以一定的速度在弹性介质中由近及远地传播出去,形成波动。 机械波产生条件:产生机械振动的振源:传播这种机械振动的弹性介质。 注意:波动是波源的振动状态或振动能量在介质中的传播,介质中的质点并不是随波 前进,只在各自的平衡位置附近往复运动。 二横波与纵波 按照质点振动方向和波的传播方向的关系,机械波可分为横波与纵波,这是波动的两 种最基本的形式。 1.横波:介质中质点振动的方向与波的传播方向垂直,表现了波峰、波谷沿波的传播方 向移动: 2.纵波:介质中质点振动的方向与波的传播方向平行,表现了介质的疏、密状态沿波传 播方向的移动。 用手上下抖动绳子时,绳子上各部分质点依次上下振动起来,这种波是横波。对于横 波,可以观察到绳子上交替出现凸起的波峰和凹下的波谷。并且它们以一定的速度沿绳传 播,这就是横波的外形特征。 将一根水平放置的长弹簧的一端固定,用手拍打另一端,各部分弹簧就依次左右振动 起来。这种波是纵波。纵波的外形特征是弹簧出现交替的“稀疏”和“稠密”区域,并且 它们以一定速度传播出去。 242
教案 第十五章 机械波 242 §1 机械波的几个概念 Some Concepts of Mechanical Wave 一 机械波的形成 机械振动在弹性介质(固体、液体和气体)内传播就形成机械波,这是因为弹性介质 内各质点之间有弹性力相互作用着。当介质中某一质点离开平衡位置时,这就发生了相变, 于是,一方面邻近质点将对它施加弹性回复力,使它回到平衡位置,并在平衡位置附近振 动起来;另一方面根据牛顿第三定律,这个质点也将对邻近质点施加弹性力,迫使邻近质 点也在自己的平衡位置附近振动起来。这样,当弹性介质中的一部分发生振动时,由于各 部分之间的弹性相互作用,振动就由近及远地传播开去,形成了振动。 弹性介质:组成介质的质点或质元之间以弹性力相互作用着,当介质中某一质点P偏 离平衡位置时,由于形变相邻质点就将对它施以弹性力作用,使它回到平衡位置。但由于 惯性的存在,P质点回到平衡位置后,又将向相反方向偏离。于是质点P就在平衡位置附件 振动起来。与此同时质点P也对其相邻质点施以弹性力作用,使相邻质点也在其平衡位置 附近振动,…,就这样振动就以一定的速度在弹性介质中由近及远地传播出去,形成波动。 机械波产生条件:产生机械振动的振源;传播这种机械振动的弹性介质。 注意:波动是波源的振动状态或振动能量在介质中的传播,介质中的质点并不是随波 前进,只在各自的平衡位置附近往复运动。 二 横波与纵波 按照质点振动方向和波的传播方向的关系,机械波可分为横波与纵波,这是波动的两 种最基本的形式。 1. 横波:介质中质点振动的方向与波的传播方向垂直,表现了波峰、波谷沿波的传播方 向移动; 2. 纵波:介质中质点振动的方向与波的传播方向平行,表现了介质的疏、密状态沿波传 播方向的移动。 用手上下抖动绳子时,绳子上各部分质点依次上下振动起来,这种波是横波。对于横 波,可以观察到绳子上交替出现凸起的波峰和凹下的波谷。并且它们以一定的速度沿绳传 播,这就是横波的外形特征。 将一根水平放置的长弹簧的一端固定,用手拍打另一端,各部分弹簧就依次左右振动 起来。这种波是纵波。纵波的外形特征是弹簧出现交替的“稀疏”和“稠密”区域,并且 它们以一定速度传播出去
教案第十五章机械波 三波长波的周期和频率波速 1波长和频率 波长用“2”表示,单位米: 横波的波长:相邻的波峰或波谷间的距离: 周期:波前进一个波长距离所需的时间: 频率:周期的倒数。 月 u=iv 2波的传播速度 波速:单位时间内波动所传播的距离。 同一波源发出的一定频率的波在不同介质中传播时,频率不变,波速不同,因而波长 不同。 注意:波速决定于介质:频率决定于波源 讨论几种介质中的波速: 绳或弦上的横波速度:“ 固体中的波速: —6+ 横波:“= G 图151长变 数该一 液体和气体中的强滨给淀连。一侣 图15-2(a)切变 对于理想气体:因阿 体变模量: 周体:B=AV 流张,8:品 图15-2b)容变 243
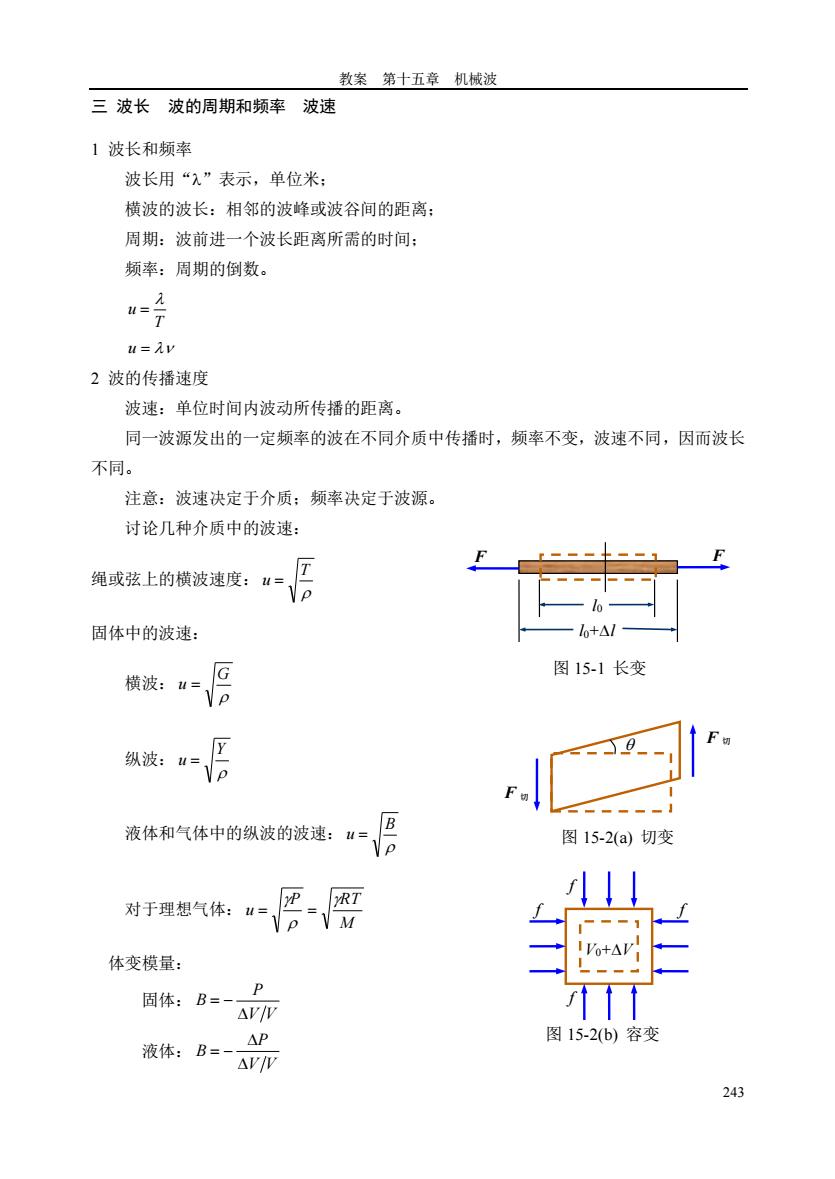
教案 第十五章 机械波 243 三 波长 波的周期和频率 波速 1 波长和频率 波长用“”表示,单位米; 横波的波长:相邻的波峰或波谷间的距离; 周期:波前进一个波长距离所需的时间; 频率:周期的倒数。 T u = u = 2 波的传播速度 波速:单位时间内波动所传播的距离。 同一波源发出的一定频率的波在不同介质中传播时,频率不变,波速不同,因而波长 不同。 注意:波速决定于介质;频率决定于波源。 讨论几种介质中的波速: 绳或弦上的横波速度: T u = 固体中的波速: 横波: G u = 纵波: Y u = 液体和气体中的纵波的波速: B u = 对于理想气体: M P RT u = = 体变模量: 固体: V V P B = − 液体: V V P B = − l0 l0+l F F 图 15-1 长变 V0+V f f f f 图 15-2(b) 容变 F 切 F 切 图 15-2(a) 切变