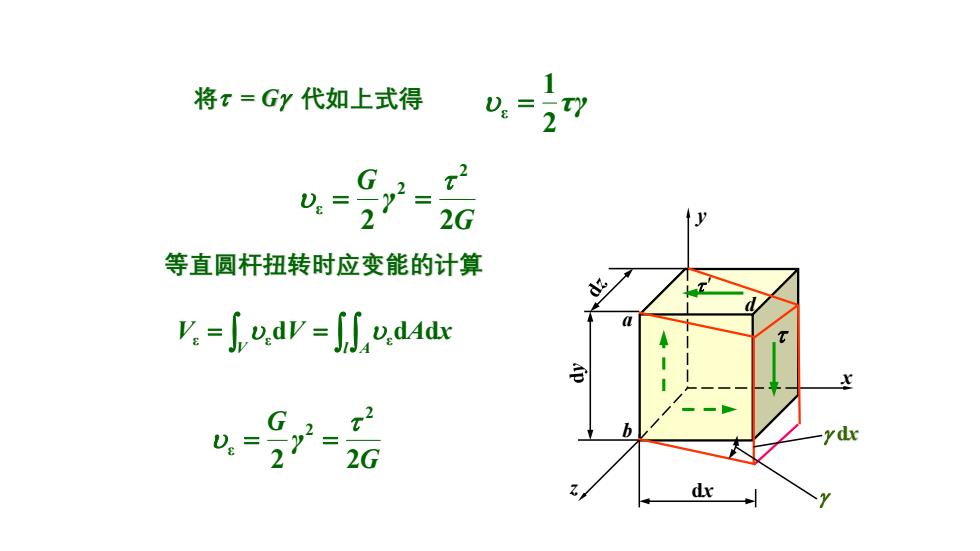
将x=Gy代如上式得 D. U= 2 2G 等直圆杆扭转时应变能的计算 v:=odv=SSo.dqde G = 2 2G
将 = G 代如上式得 dx x y z a b d dx τγ 2 1 ε = G γ G 2 2 2 2 ε = = 等直圆杆扭转时应变能的计算 = = V l A V dV dAdx ε ε ε G γ G 2 2 2 2 ε = =
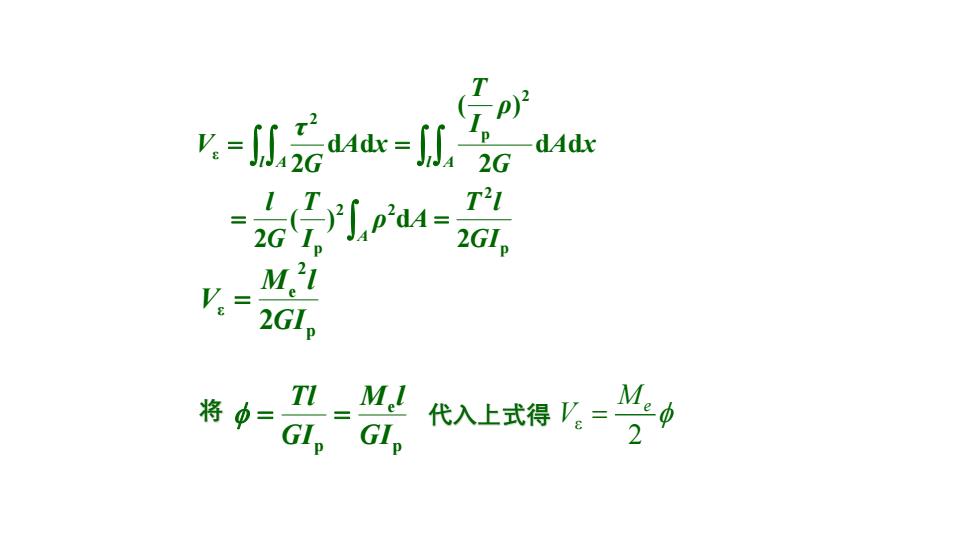
(T =G4ac=0。 dAdx 2G G.a4= T21 V:= M21 2GIp 将中= TI M GIp GIp 代入上式得店=
p 2 2 2 p 2 p 2 ε 2 ( ) d 2 d d 2 ( ) d d 2 GI T l ρ A I T G l A x G ρ I T A x G τ V A l A l A = = = = p 2 e ε 2GI M l V = 将 p e p GI M l GI Tl = = 代入上式得 ε 2 Me V =

二、变形能的应用(Application of strain energy) 1.计算变形能(Calculating strain energy) 2.利用功能原理计算变形 (Work-energy principle for calculating deflection) 例题1试求图示悬臂梁的变形能,并利用功能原理求自由端B的挠度. 解:M(x)=-F·x F23 6E1 V=)P·wg医P得 F3 WB= 3EI
二、变形能的应用(Application of strain energy) 1.计算变形能(Calculating strain energy) 2.利用功能原理计算变形 (Work-energy principle for calculating deflection) 例题1 试求图示悬臂梁的变形能,并利用功能原理求自由端B的挠度. A B F l x 解: M(x) = −F x EI F l x EI Fx x EI M x V l l 6 d 2 ( ) d 2 ( ) 2 3 0 2 2 ε = = = W F wB = 2 1 由Vε=W 得 EI Fl wB 3 3 =
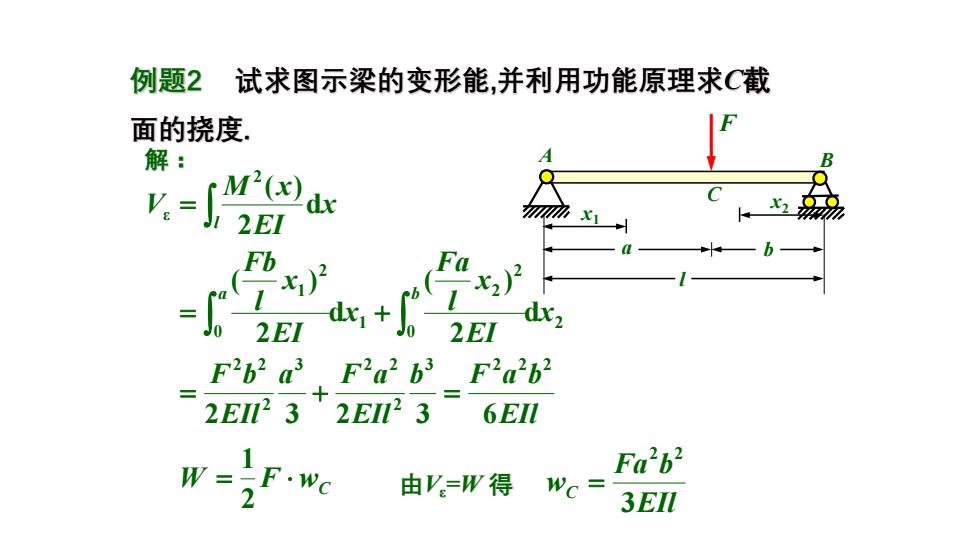
例题2 试求图示梁的变形能,并利用功能原理求C截 面的挠度 解: Fb Fa x2)月 dx+ 0 2EI F2b2 a3 F2a2 b3 F2a2b2 2EⅡ232EI123 6EIl W-F.we Fa"b2 由V=W得 Wc= 3 EIl
例题2 试求图示梁的变形能,并利用功能原理求C截 面的挠度. A B C F x1 x2 a b l 解: EIl b F a b EIl a F a EIl F b x EI x l Fa x EI x l Fb x EI M x V a b l 2 3 2 3 6 d 2 ( ) d 2 ( ) d 2 ( ) 3 2 2 2 2 3 2 2 2 2 2 2 0 2 2 1 0 2 1 2 ε = + = = + = W F wC = 2 1 EIl Fa b wC 3 2 2 由Vε=W 得 =
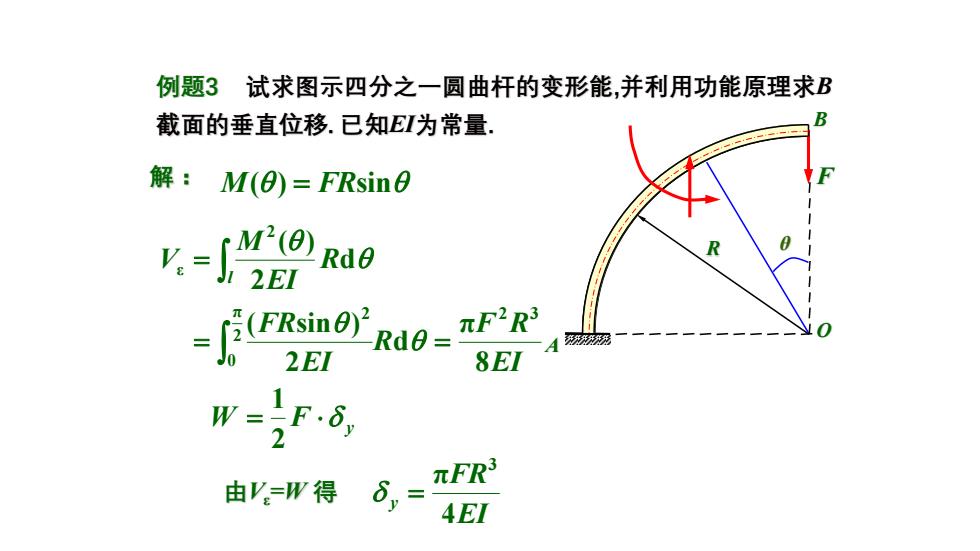
例题3试求图示四分之一圆曲杆的变形能,并利用功能原理求B 截面的垂直位移.已知E1为常量. B 解:M(0=FRsin0 片=jg9d0 -ia9- 2EI 8EI W-iF-6 由'=W得 πFR3 4EI
例题3 试求图示四分之一圆曲杆的变形能,并利用功能原理求B 截面的垂直位移. 已知EI为常量. EI F R R EI FR R EI M V l 8 π d 2 ( sin ) d 2 ( ) 2 3 2 π 0 2 2 ε = = = 解: M( ) = FRsin W F y = 2 1 EI FR y 4 π 3 = A B F O R θ 由Vε=W 得