1/2 /2 例题4以弯曲变形为例证明 应变能V只与外力的最 终值有关,而与加载过程 和加载次序无关 解: 梁中点的挠度为: F 6= MP 48EI 16EI 62=0= FL MI 梁右端的转角为: 16EI 3EI 梁的变形能为: 16
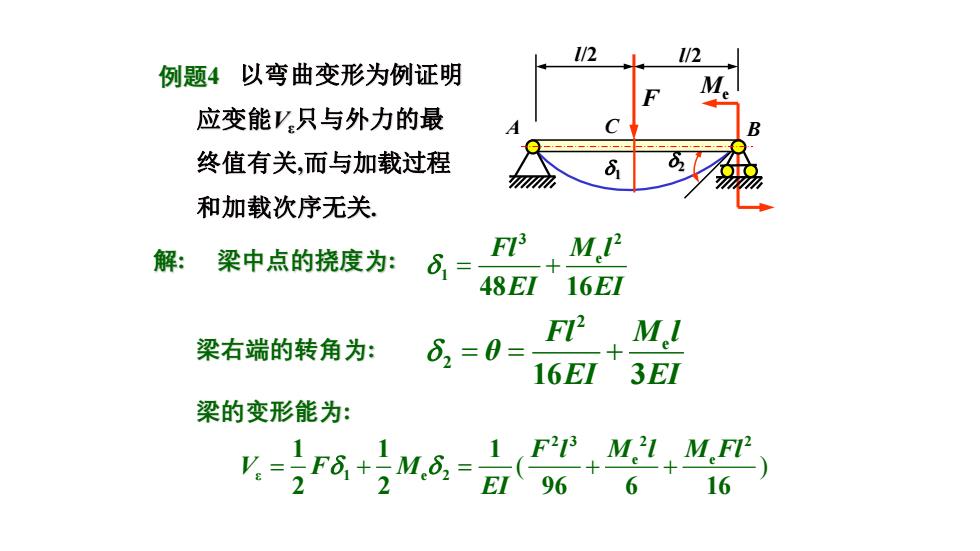
2 解: 梁中点的挠度为: 梁右端的转角为: Me = + 3 2 e 1 48 16 Fl M l EI EI = = + 2 e 2 16 3 Fl M l θ EI EI A C B F l/2 l/2 梁的变形能为: = + = + + ( ) 2 3 2 2 e e ε 1 e 2 1 1 1 2 2 96 6 16 F l M l M Fl V F M EI 1 例题4 以弯曲变形为例证明 应变能Vε只与外力的最 终值有关,而与加载过程 和加载次序无关
先加力F后,再加力偶M (1)先加力F后,C点的位移 F = 48E1 力F所作的功为 l/2 (2)力偶由零增至最后值M。 B截面的转角为0= MI 3E1 力偶M。所作的功为 2 3E
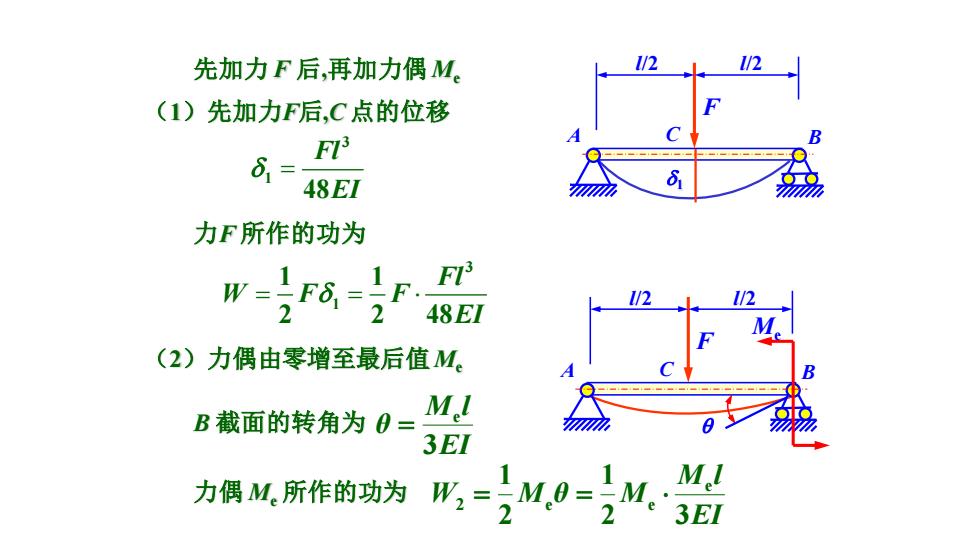
先加力 F 后,再加力偶 Me (1)先加力F后,C 点的位移 力F 所作的功为 = 3 1 48 Fl EI = = 3 1 1 1 2 2 48 Fl W F F EI (2)力偶由零增至最后值Me B 截面的转角为 EI M l θ 3 e = 力偶 Me 所作的功为 EI M l W M θ M 2 3 1 2 1 e 2 e e = = A C B F l/2 l/2 A C B F l/2 l/2 Me 1

C截面的位移为 M.12 16E1 先加上的力F所作的功为 W3=F63=F. M.12 16E7 L/2 F与力偶M所作的功为 1。F73 =F M.12 48EI 16E1 1 M.1 + M 2 3EI
先加上的力F所作的功为 C截面的位移为 3 = 2 e 3 16 M l EI = = 2 e 3 3 16 M l W F F EI A C B l/2 l/2 F与力偶Me所作的功为 EI M l M EI M l F EI Fl V F 2 3 1 2 48 16 1 e e 2 e 3 ε + = + A C B F l/2 l/2 1 Me

能量法2莫尔积分法
能量法2 莫尔积分法

§10-4莫尔定理(Mohr's theorem) 一、莫尔定理的推导(Derivation of mohr's theorem) 用附加力法可以求出杆件任意位置任何方向的位移。假设 杆件承受外荷载为F,附加力为F,则在F和F单独作用下杆件的 弯矩分别为M(x)和M'(x)。运用叠加原理可求出杆件在F和F共 同作用下的弯矩为M(x)+M'(x)则 d.=tM)aMa牛k= M(x)M'(d El oF' af, 式中第一项中的M'(x)是由虚设力F'引起的,所以在积分前可先令其等于零 aM'(x) 第二项F' 实际上就是对应于所求位移方向的单位力作用下的弯矩,所以 6M== M(xM(dx 莫尔定理
§10-4 莫尔定理(Mohr’s theorem) 一、莫尔定理的推导(Derivation of mohr’s theorem) 用附加力法可以求出杆件任意位置任何方向的位移。假设 杆件承受外荷载为F,附加力为F‘ ,则在F和F‘单独作用下杆件的 弯矩分别为M(x)和M‘(x)。运用叠加原理可求出杆件在F和F‘共 同作用下的弯矩为 M (x) + M (x ,则 ) ( ) ( ) dx F M x EI M x dx F M x M x EI M x M x l l M = + + == ( ) ( ) ( ) ( ) ( ) ( ) 第二项 F 实际上就是对应于所求位移方向的单位力作用下的弯矩,所以 M x ( ) 式中第一项中的 M (x) 是由虚设力 F 引起的,所以在积分前可先令其等于零 dx EI M x M x l M === ( ) ( ) 莫尔定理