
Rolle定理 若函数f在a,b]上连续,在(a,b)内可导,f(a)=f(b),则归5∈(a,b) 使得f'(5)=0 证明:记f在[a,b]上的最大最小值分别为M,m,如果M=m,则f为常值 函数,定理显然成立。如果M≠m,由于f(a)=f(b),所以M与m必然 有一个在(a,b)内达到,定理得证
[ , ] ( , ) ( ) ( ), ( , ) ( ) 0 f a b a b f a f b a b f 若函数 在 上连续,在 内可导, 则 使得 [ , ] , , , , ( ) ( ) ( , ) f a b M m M m f M m f a f b M m a b 证明:记 在 上的最大最小值分别为 如果 则 为常值 函数,定理显然成立。如果 由于 ,所以 与 必然 有一个在 内达到,定理得证。 Rolle定理

Rolle,Michel 罗尔是法国数学家,1652年4月21日生于昂贝尔特, I719年1川月8日辛于巴黎。 罗尔在数学上的成就主要是在代数方面,专长于丢香 图方程的研究。罗尔于9!年在题为《任意次方程的 一个解法的证明》的论文中指出了:在多项式方程的 两个相邻的实根之间,方程至少有一个根。在一百多 年后,I846年尤斯托(Giusto Bellavitis)将这一定理推 广到可微函数,尤斯托还把此定理命名为罗尔定理。 The calculus is a collection of ingenious fallacies
Rolle,Michel 罗尔是法国数学家,1652年4月21日生于昂贝尔特, 1719年11月8日卒于巴黎。 罗尔在数学上的成就主要是在代数方面,专长于丢番 图方程的研究。 罗尔于1691年在题为《任意次方程的 一个解法的证明》的论文中指出了:在多项式方程 的 两个相邻的实根之间,方程 至少有一个根。在一百多 年后,1846年尤斯托(Giusto Bellavitis)将这一定理推 广到可微函数,尤斯托还把此定理命名为罗尔定理。 The calculus is a collection of ingenious fallacies

例 证明方程x3+2x+1=0在区间(-1,0)内有且只有一个实根。 证明若函数f:[0,→R在[0,]上连续,在(0,1)内可导,并且 f四=0,则至少存在一个ce(0,1),f(c)=-f
例 3 证明方程x x 2 1 0 1,0 在区间 内有且只有一个实根。 : 0,1 0,1 0 1 (1) 0 0,1 , f f c f c f c c 证明若函数 在 上连续,在 ,内可导,并且 ,则至少存在一个
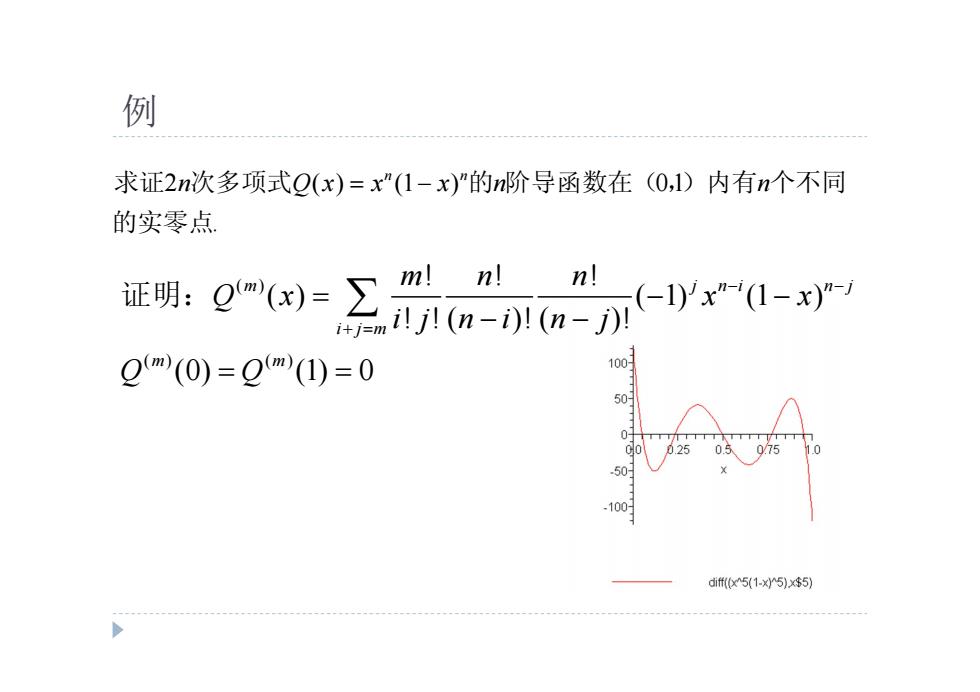
例 求证2n次多项式Q(x)=x"(1-x)”的n阶导函数在(0,l)内有n个不同 的实零点 m! n! t明:e(三a”anr1- n! 2m(0)=Qm(1)=0 100时 50 50 .100 df0x5(1-x05)x$5)
例 2 ( ) (1 ) 0 1 . n n 求证 n Q x x x n n 次多项式 的 阶导函数在( ,)内有 个不同 的实零点 ( ) ( ) ( ) ! ! ! ( ) ( 1) (1 ) ! ! ( )! ( )! (0) (1) 0 m j n i n j i j m m m m n n Q x x x i j n i n j Q Q 证明:

Lagrange中值定理 若函数f在[a,b]上连续,在(a,b)内可导,则归c∈(a,b), f(b)-f(a) b-a =f'(c) 证明:构造辅助函数 Tangent parallel to chord F(x)-f(b)-f(@x-f(x) b-a Slopef"(c) B 直接应用Rolle定理 Slope fb)-f(a) b-a y X a b y=f(x)
Lagrange中值定理 [ , ] ( , ) ( , ), ( ) ( ) ( ) f a b a b c a b f b f a f c b a 若函数 在 上连续,在 内可导,则 ( ) ( ) ( ) ( Roll ) , e f b f a F x x f x b a 证明:构造辅助函数 直接应用 定理