
2-5用求解器进行几何构造分析 数据文档从略。采用智能求解,结果如下: 对图2-5-2a: 对图2-5-2b: 刚片1由以下杆件构成:(1)(2) 本题用两刚片和三刚片法则无法求解 刚片2由以下杆件构成:(5)(6) 由三刚片规则,将单元(8)看成一刚片,另两刚片 为:1、2,可得一大刚片1 图2-5-2b在图2-5-2a的基础上稍加变化,但题目求解性质发生了改变,无法再用常规的 三刚片法则求解,这是智能求解的局限。采用自动求解,图2-5-2a和图2-5-2b均为无多余约 束的几何不变体系。由于图2-5-2b中有一些复链杆,因此用零载法时涉及弯矩和剪力,不是 很方便。 例25-3试用求解器分析图2-5-3所示的几何构造。 (3) (1) (3) (1) 4) (5) (6 (6) (a) 图2-5-3例2-5-3图 数据文档从略。先采用智能求解,结果为: 对图2-5-3a: 对图2-5-3b 将大地看成一刚片,记为刚片0 将大地看成一刚片,记为刚片0 刚片1由以下杆件构成:(1)(2)(⑦) 刚片1由以下杆件构成:(1)(2)(7 由三刚片规则,将单元(⑤)看成一刚片,另两 将刚片0看成第一个刚片 刚片为:0、1,可得一大刚片0 将刚片1看成第二个刚片 将杆件(⑤)看成第三个刚片 由三刚片规则,连接三刚片的三个(虚)较过 一直线,瞬变体系 图2-5-3b仅将图2-5-3a中的结点6的位置稍加调整,但使平面体系性质发生了改变,求 解器对这两种情况也分别给出了正确的计算步骤和结论。 为了获得图2-5-3b所示的机构运动模态,可采用自动求解,其运动模态如图2-5-4所示。 3
§2-5 用求解器进行几何构造分析 数据文档从略。采用智能求解,结果如下: 对图 2-5-2a: 刚片 1 由以下杆件构成: (1) (2) 刚片 2 由以下杆件构成: (5) (6) 由三刚片规则,将单元(8)看成一刚片,另两刚片 为: 1、2,可得一大刚片 1 对图 2-5-2b: 本题用两刚片和三刚片法则无法求解 图 2-5-2b 在图 2-5-2a 的基础上稍加变化,但题目求解性质发生了改变,无法再用常规的 三刚片法则求解,这是智能求解的局限。采用自动求解,图 2-5-2a 和图 2-5-2b 均为无多余约 束的几何不变体系。由于图 2-5-2b 中有一些复链杆,因此用零载法时涉及弯矩和剪力,不是 很方便。 例 2-5-3 试用求解器分析图 2-5-3 所示的几何构造。 图2-5-3 例2-5-3图 数据文档从略。先采用智能求解,结果为: 对图 2-5-3a: 将大地看成一刚片,记为刚片 0 刚片 1 由以下杆件构成: (1) (2) (7) 由三刚片规则,将单元 (5) 看成一刚片,另两 刚片为: 0 、1,可得一大刚片 0 对图 2-5-3b: 将大地看成一刚片,记为刚片 0 刚片 1 由以下杆件构成: (1) (2) (7) 将刚片 0 看成第一个刚片 将刚片 1 看成第二个刚片 将杆件 (5) 看成第三个刚片 由三刚片规则,连接三刚片的三个(虚)铰过 一直线,瞬变体系 图 2-5-3b 仅将图 2-5-3a 中的结点 6 的位置稍加调整,但使平面体系性质发生了改变,求 解器对这两种情况也分别给出了正确的计算步骤和结论。 为了获得图 2-5-3b 所示的机构运动模态,可采用自动求解,其运动模态如图 2-5-4 所示。 3
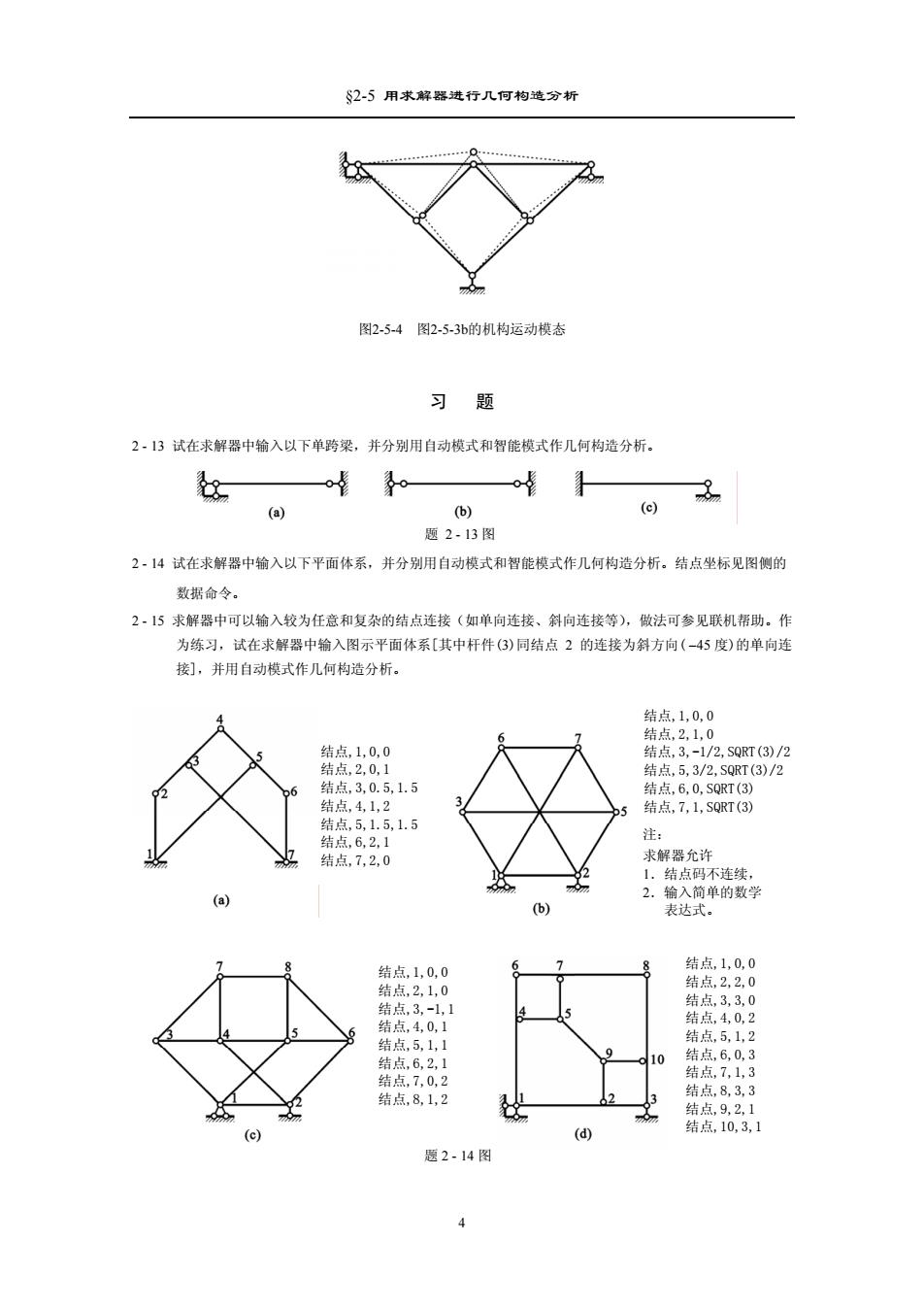
2-5用求解器进行几何构造分析 图2-5-4图2-5-3b的机构运动模态 习题 2-13试在求解器中输入以下单跨梁,并分别用自动模式和智能模式作几何构造分析。 (a) (b) (c) 题2.13图 2,14试在求解器中输入以下平面体系,并分别用自动模式和智能模式作几何构造分析。结点坐标见图侧的 数据命令。 2,15求解器中可以输入较为任意和复杂的结点连接(如单向连接、斜向连接等),做法可参见联机帮助。作 为练习,试在求解器中输入图示平面体系[其中杆件(3)同结点2的连接为斜方向(-45度)的单向连 接],并用自动模式作几何构造分析。 结点,1,0,0 结点,2,1,0 结点,1,0,0 结点,3,-1/2,SQRT(3)/2 结点,2,0,1 结点,5,3/2,SQRT(3)/2 结点,3,0.5,1.5 结点,6,0,SQRT(3) 结点,4,1,2 5 结点,7,1,SQRT(3) 结点,5,1.5,1.5 结点,6,2.1 注: 结点,7,2,0 求解器允许 1.结点码不连续, (a) 2.输入简单的数学 (b) 表达式。 结点,1,0,0 结点,1,0,0 结点,2,1,0 结点,2,2.0 结点,3,-1,1 结点,3,3,0 结点,4,0,2 结点,4,0,1 结点,5,1,1 结点,5,1,2 结点,6,2,1 10 结点,6,0,3 结点,7,0,2 结点,7,1,3 结点,8,1,2 结点,8,3,3 结点,9,2,1 (c) (d) 结点,10,3,1 题2-14图 4
§2-5 用求解器进行几何构造分析 图2-5-4 图2-5-3b的机构运动模态 习 题 2 - 13 试在求解器中输入以下单跨梁,并分别用自动模式和智能模式作几何构造分析。 题 2 - 13 图 2 - 14 试在求解器中输入以下平面体系,并分别用自动模式和智能模式作几何构造分析。结点坐标见图侧的 数据命令。 2 - 15 求解器中可以输入较为任意和复杂的结点连接(如单向连接、斜向连接等),做法可参见联机帮助。作 为练习,试在求解器中输入图示平面体系[其中杆件(3)同结点 2 的连接为斜方向( 度)的单向连 接],并用自动模式作几何构造分析。 −45 结点,1,0,0 结点,2,0,1 结点,3,0.5,1.5 结点,4,1,2 结点,5,1.5,1.5 结点,6,2,1 结点,7,2,0 结点,1,0,0 结点,2,1,0 结点,3,-1/2,SQRT(3)/2 结点,5,3/2,SQRT(3)/2 结点,6,0,SQRT(3) 结点,7,1,SQRT(3) 注: 求解器允许 1.结点码不连续, 2.输入简单的数学 表达式。 结点,1,0,0 结点,2,1,0 结点,3,-1,1 结点,4,0,1 结点,5,1,1 结点,6,2,1 结点,7,0,2 结点,8,1,2 结点,1,0,0 结点,2,2,0 结点,3,3,0 结点,4,0,2 结点,5,1,2 结点,6,0,3 结点,7,1,3 结点,8,3,3 结点,9,2,1 结点,10,3,1 题 2 - 14 图 4

2-5用求解器进行几何构造分析 (4) 结点,1,0,0 (2) ● 5K 结点,2,0,1 结点,3,0,2 (3) 结点,4,1,0 结点,5,1,1.5 5) (1) 注: 求解器对大小写 字母均接受。 题2.15图 5
§2-5 用求解器进行几何构造分析 结点,1,0,0 结点,2,0,1 结点,3,0,2 结点,4,1,0 结点,5,1,1.5 题 2 - 15 图 注: 求解器对大小写 字母均接受。 5