
S2-4在求解器中输入平面结构体系 接。这种处理的好处是可以避免结点的重复编码(如本书中矩阵位移法中所介绍的),同时可 以方便地构造各种复杂的组合结点。 另外,在定义位移约束时,结点处的支座约束也是首先加在虚拟刚结点上,再通过虚拟 刚结点施加给其他相关的杆端。 有了虚拟刚结点的概念,其他的具体做法都己比较显而易见,通过具体例题便很容易搞 懂。因此,以下基本上以例题来代替叙述。疑问之处,可以参见求解器的联机帮助。 3.输入结构体系 欲输入一个结构体系,首先在“编辑器”中打开一个新文件,然后输入命令。在求解器 中输入命令有两种方法: (1)利用“命令”菜单中的子菜单,打开相应的对话框,在对话框中根据提示和选项输入 命令。 (2)在文件中直接键入命令行。 第(1)种方法可以免除用户记忆命令格式,且可以利用对话框中的预览功能随时修正输入 的命令。如果用户对命令格式较熟悉,则直接键入命令更为快捷。本盘在附录中给出了所有 命令的语法规则和格式,需要时可以查阅。 修改命令也有两种方法: 1)将光标置于要修改的命令行,单击工具栏上的“修改”按钮(或在“命令”菜单下选 “修改”子菜单),则求解器将自动打开相应的命令对话框,对话框中的各选项再现了该条命 令中的各个参数,用户可以查看或修改。 2)在文件中直接修改命令行。 求解器中的每一条命令都由一关键词作先导,自版本V1.5开始,在保留原来的英文关键 词的同时,允许使用相应的中文关键词,在功能上它们是等效的。英文关键词键入方便,中 文关键词易读易辨。求解器中默认的选择是中文关键词,如果希望用英文关键词的话,可在 “查看”菜单下去除“中文关键词”的选项。本盘的附录中给出了所有命令的中英文关键词 的对照,需要时可以查询。本盘中大都采用中文关键词。 以下例题中,首先给出完成的命令数据文档,同时给出输入后的结构体系的图例,然后 对个别命令行的输入作简要说明。 例2-4-1在求解器中输入图2-4-6a所示的结构体系。 7 (5) 5 (4) (6 (2) 1) (3 1 m 1.5m (a)平面结构 (b)输入后显示的结构 图2-4-6结构的数值化定义
§2-4 在求解器中输入平面结构体系 接。这种处理的好处是可以避免结点的重复编码(如本书中矩阵位移法中所介绍的),同时可 以方便地构造各种复杂的组合结点。 另外,在定义位移约束时,结点处的支座约束也是首先加在虚拟刚结点上,再通过虚拟 刚结点施加给其他相关的杆端。 有了虚拟刚结点的概念,其他的具体做法都已比较显而易见,通过具体例题便很容易搞 懂。因此,以下基本上以例题来代替叙述。疑问之处,可以参见求解器的联机帮助。 3. 输入结构体系 欲输入一个结构体系,首先在“编辑器”中打开一个新文件,然后输入命令。在求解器 中输入命令有两种方法: (1)利用“命令”菜单中的子菜单,打开相应的对话框,在对话框中根据提示和选项输入 命令。 (2)在文件中直接键入命令行。 第(1)种方法可以免除用户记忆命令格式,且可以利用对话框中的预览功能随时修正输入 的命令。如果用户对命令格式较熟悉,则直接键入命令更为快捷。本盘在附录中给出了所有 命令的语法规则和格式,需要时可以查阅。 修改命令也有两种方法: 1) 将光标置于要修改的命令行,单击工具栏上的“修改”按钮(或在“命令”菜单下选 “修改”子菜单),则求解器将自动打开相应的命令对话框,对话框中的各选项再现了该条命 令中的各个参数,用户可以查看或修改。 2)在文件中直接修改命令行。 求解器中的每一条命令都由一关键词作先导,自版本 v1.5 开始,在保留原来的英文关键 词的同时,允许使用相应的中文关键词,在功能上它们是等效的。英文关键词键入方便,中 文关键词易读易辨。求解器中默认的选择是中文关键词,如果希望用英文关键词的话,可在 “查看”菜单下去除“中文关键词”的选项。本盘的附录中给出了所有命令的中英文关键词 的对照,需要时可以查询。本盘中大都采用中文关键词。 以下例题中,首先给出完成的命令数据文档,同时给出输入后的结构体系的图例,然后 对个别命令行的输入作简要说明。 例 2-4-1 在求解器中输入图 2-4-6a 所示的结构体系。 图 2-4-6 结构的数值化定义 3

S2-4在求解器中输入平面结构体系 解输入后的结构如图24-6b所示,命令数据文档如下,其中左边和右边分别为中、英文 关键词命令数据文档。 结点,1,0,0 N,1,0,0 结点,2,0,1 N,2,0,1 结点,3,1,1 N,3,1,1 结点,4,1,0 N,4,1,0 结点,5,1,2 N,5,1,2 结点,6,2.5,0 N,6,2.5,0 结点,7,2.5,2.5 N,7,2.5,2.5 单元,1,2,1,1,0,1,1,1 E,1,2,1,1,0,1,1,1 单元,2,3,1,1,1,1,1,0 E,2,3,1,1,1,1,1,0 单元,4,3,1,1,0,1,1,1 E,4,3,1,1,0,1,1,1 单元,3,5,1,1,1,1,1,1 E,3,5,1,1,1,1,1,1 单元,5,7,1,1,1,1,1,0 E,5,7,1,1,1,1,1,0 单元,6,7,1,1,1,1,1,0 E,6,7,1,1,1,1,1,0 结点支承,1,4,0,0,0 NSUPT,1,4,0,0,0 结点支承,4,4,0,0,0 NSUPT,4,4,0,0,0 结点支承,6,6,0,0,0,0 NSUPT,6,6,0,0,0,0 END END 以上命令数据中主要有三种命令:结点定义、单元定义、结点支承定义。下面分别讨论 如何用对话框输入这些命令。 (1)结点定义 以第一行命令“结点,1,0,0”为例:其中“结点”或“N”为关键词:后面的1为结点码: 0,0为整体坐标值。用对话框输入该命令的步骤如下: )在“命令”菜单下选择“结点”子菜单,打开结点对话框:此时,默认的命令选择是 结点定义。 2)在“结点码”下拉框中输入(或从下拉选项中选)1。 3)在“坐标x”和“y”下拉框中分别输入0,0。 4)单击“预览”按钮,可以在观览器中看到结点1的显示。 5)若不满意,可以修改以上输入。 6)单击“应用”按钮,将命令写到文档上。 7)可以继续输入下一个命令。 8)完成输入后,单击“关闭”按钮,关闭结点对话框。 此时,可以在文档上看到已输入的命令行,同时观览器中会同步显示出该结点。其余结点的 输入类似。 (2)单元定义 在结点定义命令后面的是单元定义命令。此时,要用到虚拟刚结点的概念。第一行单元 定义命令为:“单元,1,2,1,1,0,1,1,1”:其中关键词“单元”或“E”后面的1,2为单元两端 的结点码:随后的6个数据是两端点与虚拟刚结点1,2的连接码。用对话框输入该命令步骤 如下: 1)在“命令”菜单下选择“单元”子菜单,打开单元对话框:此时,默认的命令选择 是单元定义。 2)单元编码按照输入顺序自动排列,因此没有单元码输入选项。 3)在“杆端1”的“连接结点”处输入1,“连接方式”选“铰结
§2-4 在求解器中输入平面结构体系 解 输入后的结构如图 2-4-6b 所示,命令数据文档如下,其中左边和右边分别为中、英文 关键词命令数据文档。 结点,1,0,0 结点,2,0,1 结点,3,1,1 结点,4,1,0 结点,5,1,2 结点,6,2.5,0 结点,7,2.5,2.5 单元,1,2,1,1,0,1,1,1 单元,2,3,1,1,1,1,1,0 单元,4,3,1,1,0,1,1,1 单元,3,5,1,1,1,1,1,1 单元,5,7,1,1,1,1,1,0 单元,6,7,1,1,1,1,1,0 结点支承,1,4,0,0,0 结点支承,4,4,0,0,0 结点支承,6,6,0,0,0,0 END N,1,0,0 N,2,0,1 N,3,1,1 N,4,1,0 N,5,1,2 N,6,2.5,0 N,7,2.5,2.5 E,1,2,1,1,0,1,1,1 E,2,3,1,1,1,1,1,0 E,4,3,1,1,0,1,1,1 E,3,5,1,1,1,1,1,1 E,5,7,1,1,1,1,1,0 E,6,7,1,1,1,1,1,0 NSUPT,1,4,0,0,0 NSUPT,4,4,0,0,0 NSUPT,6,6,0,0,0,0 END 以上命令数据中主要有三种命令:结点定义、单元定义、结点支承定义。下面分别讨论 如何用对话框输入这些命令。 (1)结点定义 以第一行命令“结点,1,0,0”为例;其中“结点”或“N”为关键词;后面的 1 为结点码; 0,0 为整体坐标值。用对话框输入该命令的步骤如下: 1)在“命令”菜单下选择“结点”子菜单,打开结点对话框;此时,默认的命令选择是 结点定义。 2)在“结点码”下拉框中输入(或从下拉选项中选)1。 3)在“坐标 x”和“y”下拉框中分别输入 0,0。 4)单击“预览”按钮,可以在观览器中看到结点 1 的显示。 5)若不满意,可以修改以上输入。 6)单击“应用”按钮,将命令写到文档上。 7)可以继续输入下一个命令。 8)完成输入后,单击“关闭”按钮,关闭结点对话框。 此时,可以在文档上看到已输入的命令行,同时观览器中会同步显示出该结点。其余结点的 输入类似。 (2)单元定义 在结点定义命令后面的是单元定义命令。此时,要用到虚拟刚结点的概念。第一行单元 定义命令为:“单元,1,2,1,1,0,1,1,1”;其中关键词“单元”或“E”后面的 1,2 为单元两端 的结点码;随后的 6 个数据是两端点与虚拟刚结点 1,2 的连接码。用对话框输入该命令步骤 如下: 1) 在“命令”菜单下选择“单元”子菜单,打开单元对话框;此时,默认的命令选择 是单元定义。 2) 单元编码按照输入顺序自动排列,因此没有单元码输入选项。 3) 在“杆端 1”的“连接结点”处输入 1,“连接方式”选“铰结”。 4

S2-4在求解器中输入平面结构体系 4)在“杆端2”的“连接结点”处输入2,“连接方式”选“刚结”。 5)若要预览,可以单击“预览”。 6)单击“应用”按钮,将命令写到文档上,而后可以继续下一个命令。 7)单击“关闭”按钮,关闭对话框。 此时,可以在文档上看到已输入的命令行,同时观览器中会显示出该单元。其余单元的输入 类似。在观览器的“显示”菜单中,激活“单元方向”,则在各单元上可以看到表示单元方向 的箭头;在观览器的“标注”菜单中,可以激活或取消“单元长度”、“单元码”等选项。 (3)结点支承定义 在单元定义命令后面的是结点支承定义命令。此时,也要用到虚拟刚结点的概念。第一 行结点支承命令为:“结点支承,1,4,0,0,0”:其中关键词“结点支承”或“NSUPT”后面的1 表示结点1:4代表第4类支承(即第3种铰支座):随后的0代表支座方位为水平放置(无 转动):0,0表示支座无水平和竖向位移。用对话框输入该命令步骤如下: 1)在“命令”菜单下选择“位移约束”子菜单,打开支座约束对话框: 2)默认的约束类型是“结点支座”,在“结点码”下拉框中输入1: 3)在“支座类型”处选4,“支座性质”保留默认的“刚性”,其余的均为0: 4)其余的同单元定义的第5)~7)。 此时,可以在文档上看到命令行,同时观览器中会显示出该支座。最后一行结点支座命令“结 点支承,6,6,0,0,0,0”在末尾多了一个0,这是由于该支座为固定支座,最后一个0表示该支 座无转角
§2-4 在求解器中输入平面结构体系 4) 在“杆端 2”的“连接结点”处输入 2,“连接方式”选“刚结”。 5) 若要预览,可以单击“预览”。 6) 单击“应用”按钮,将命令写到文档上,而后可以继续下一个命令。 7) 单击“关闭”按钮,关闭对话框。 此时,可以在文档上看到已输入的命令行,同时观览器中会显示出该单元。其余单元的输入 类似。在观览器的“显示”菜单中,激活“单元方向”,则在各单元上可以看到表示单元方向 的箭头;在观览器的“标注”菜单中,可以激活或取消“单元长度”、“单元码”等选项。 (3) 结点支承定义 在单元定义命令后面的是结点支承定义命令。此时,也要用到虚拟刚结点的概念。第一 行结点支承命令为:“结点支承,1,4,0,0,0”;其中关键词“结点支承”或“NSUPT”后面的 1 表示结点 1;4 代表第 4 类支承(即第 3 种铰支座);随后的 0 代表支座方位为水平放置(无 转动);0,0 表示支座无水平和竖向位移。用对话框输入该命令步骤如下: 1) 在“命令”菜单下选择“位移约束”子菜单,打开支座约束对话框; 2) 默认的约束类型是“结点支座”,在“结点码”下拉框中输入 1; 3) 在“支座类型”处选 4,“支座性质”保留默认的“刚性”,其余的均为 0; 4) 其余的同单元定义的第 5)~7)。 此时,可以在文档上看到命令行,同时观览器中会显示出该支座。最后一行结点支座命令“结 点支承,6,6,0,0,0,0”在末尾多了一个 0,这是由于该支座为固定支座,最后一个 0 表示该支 座无转角。 5

$2-5用求解器进行几何构造分析 S2-5用求解器进行几何构造分析 1.几何构造分析的计算机方法 进行几何构造分析时采用的方法可分为两类:一类是适用于手算的经典方法,另一类是 适用于计算机的程序方法。 在前边的学习中,学到的用三角形组成规律进行几何构造分析的方法是一种适用于手算 的经典方法。这种方法机智灵巧,但不便于编制计算机程序:能够简捷地处理工程中常用的 杆件体系问题,但难于处理复杂的杆件体系问题。 在求解器中自然采用计算机方法。关于这种方法的详细内容将在《程序结构力学》中介 绍,本盘主要将求解器当作工具使用,并对其解题思路作一简述。 思路一一把平面体系的几何构造分析问题表示为一组齐次线性代数方程问题,然后根 据方程组的解的性质可得出几何构造分析的有关结论。 求解步骤: (1)拆除体系中的各个约束,以体系的独立的结点位移作为基本未知量,共有N个。 (2)再把约束加上去,也就是在待求位移之间建立约束条件,得到以N个结点位移为未知 量的M个齐次线性代数方程。 (3)由方程组求解待定位移。根据方程组系数矩阵的阶数和秩,可以确定解的性质。 如方程组有唯一的平凡解(待定位移都是零),则体系为几何不变:反之则为可变。 如方程组系数矩阵的秩小于约束方程的个数,则体系具有多余约束。 2.两种求解模式 对于几何构造分析,求解器具两种求解模式: (1)自动求解 可以对任意的平面体系进行几何构造分析:判断几何可变还是不变:对于可变体系,给 出体系自由度数,指出是常变还是瞬变,并静态或动画显示机构运动模态:若体系有多余约 束,给出多余约束的数目。 (2)智能求解 按两刚片或三刚片法则求解,给出具体的求解步骤。对于无法用三角形法则求解的问题, 给出提示。 自动求解可用来求解所有问题,也是一个方便的研究工具:而智能求解可以模仿人工手 算给出解题思路与步骤,对学生很有帮助。以下通过例题来分别加以说明和介绍。 例2-5-1试用两种求解模式分析图2-5-1a的几何构造,其中结点5、6是组合结点。 解首先,考虑自动求解。输入后的命令文档为 TITLE,例2-5-1 (a) (5) 结点,1,0,0 结点,2,0.4,0 (8) 9) 结点,3,0.6,0 (11)8 结点,4,1,0 (4) (6) 结点,5,0.2,0.5 (7) (10) 结点,6,0.8,0.5 结点,7,0.35,0.3 (1) (2) (3) 结点,8,0.65,0.3 单元,1,2,1,1,0,1,1,0
§2-5 用求解器进行几何构造分析 §2-5 用求解器进行几何构造分析 1. 几何构造分析的计算机方法 进行几何构造分析时采用的方法可分为两类:一类是适用于手算的经典方法,另一类是 适用于计算机的程序方法。 在前边的学习中,学到的用三角形组成规律进行几何构造分析的方法是一种适用于手算 的经典方法。这种方法机智灵巧,但不便于编制计算机程序;能够简捷地处理工程中常用的 杆件体系问题,但难于处理复杂的杆件体系问题。 在求解器中自然采用计算机方法。关于这种方法的详细内容将在《程序结构力学》中介 绍,本盘主要将求解器当作工具使用,并对其解题思路作一简述。 思路 —— 把平面体系的几何构造分析问题表示为一组齐次线性代数方程问题,然后根 据方程组的解的性质可得出几何构造分析的有关结论。 求解步骤: (1) 拆除体系中的各个约束,以体系的独立的结点位移作为基本未知量,共有 N 个。 (2) 再把约束加上去,也就是在待求位移之间建立约束条件,得到以 N 个结点位移为未知 量的 M 个齐次线性代数方程。 (3) 由方程组求解待定位移。根据方程组系数矩阵的阶数和秩,可以确定解的性质。 如方程组有唯一的平凡解(待定位移都是零),则体系为几何不变;反之则为可变。 如方程组系数矩阵的秩小于约束方程的个数,则体系具有多余约束。 2. 两种求解模式 对于几何构造分析,求解器具两种求解模式: (1) 自动求解 可以对任意的平面体系进行几何构造分析:判断几何可变还是不变;对于可变体系,给 出体系自由度数,指出是常变还是瞬变,并静态或动画显示机构运动模态;若体系有多余约 束,给出多余约束的数目。 (2) 智能求解 按两刚片或三刚片法则求解,给出具体的求解步骤。对于无法用三角形法则求解的问题, 给出提示。 自动求解可用来求解所有问题,也是一个方便的研究工具;而智能求解可以模仿人工手 算给出解题思路与步骤,对学生很有帮助。以下通过例题来分别加以说明和介绍。 例 2-5-1 试用两种求解模式分析图 2-5-1a 的几何构造,其中结点 5、6 是组合结点。 解 首先,考虑自动求解。输入后的命令文档为 TITLE,例 2-5-1 结点,1,0,0 结点,2,0.4,0 结点,3,0.6,0 结点,4,1,0 结点,5,0.2,0.5 结点,6,0.8,0.5 结点,7,0.35,0.3 结点,8,0.65,0.3 单元,1,2,1,1,0,1,1,0 1
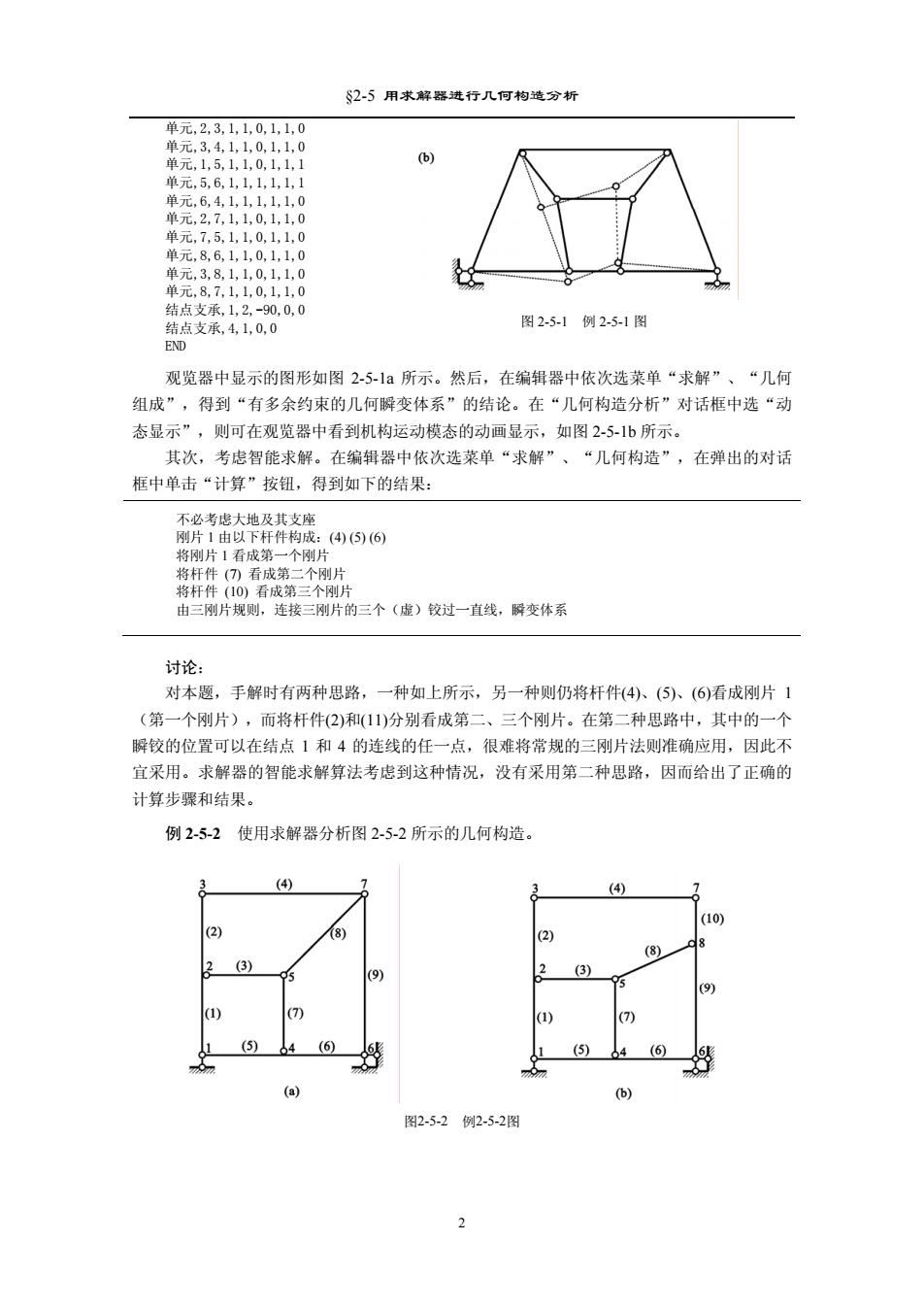
2-5用求解器进行几何构造分析 单元,2,31,1,0,1,1,0 单元,3,4,1,1,0,1,1,0 单元,1,5,1,1,0,1,1,1 单元,5,6,1,1,1,1,1,1 单元,6,4,1,1,1,1,1,0 单元,2,7,1,1,0,1,1,0 单元,7,5,1,1,0,1,1,0 单元,8,6,1,1,0,1,1,0 单元,3,8,1,1,0,1,10 单元,8,7,1,1,0,1,1,0 结点支承,1,2,-90,0,0 结点支承,4,1,0,0 图2-5-1例2-5-1图 END 观览器中显示的图形如图2-5-1a所示。然后,在编辑器中依次选菜单“求解”、“几何 组成”,得到“有多余约束的几何瞬变体系”的结论。在“几何构造分析”对话框中选“动 态显示”,则可在观览器中看到机构运动模态的动画显示,如图2-5-1b所示。 其次,考虑智能求解。在编辑器中依次选菜单“求解”、“几何构造”,在弹出的对话 框中单击“计算”按钮,得到如下的结果: 不必考虑大地及其支座 刚片1由以下杆件构成:(4)(⑤)(6) 将刚片1看成第一个刚片 将杆件()看成第二个刚片 将杆件(10)看成第三个刚片 由三刚片规则,连接三刚片的三个(虚)铰过一直线,瞬变体系 讨论: 对本题,手解时有两种思路,一种如上所示,另一种则仍将杆件(4)、(⑤)、(6)看成刚片1 (第一个刚片),而将杆件(2)和(11)分别看成第二、三个刚片。在第二种思路中,其中的一个 瞬铰的位置可以在结点1和4的连线的任一点,很难将常规的三刚片法则准确应用,因此不 宜采用。求解器的智能求解算法考虑到这种情况,没有采用第二种思路,因而给出了正确的 计算步骤和结果。 例2-5-2使用求解器分析图2-5-2所示的几何构造。 (4) (4) (10) (2) (8) (2) 8 (8) 2 (3) (9) 2 (3) (9) (1) (7) (1) (7) (5) 4 (6) 6 (5) 4 (6) 6 (a) (b) 图2-5-2 例2-5-2图 2
§2-5 用求解器进行几何构造分析 图 2-5-1 例 2-5-1 图 单元,2,3,1,1,0,1,1,0 单元,3,4,1,1,0,1,1,0 单元,1,5,1,1,0,1,1,1 单元,5,6,1,1,1,1,1,1 单元,6,4,1,1,1,1,1,0 单元,2,7,1,1,0,1,1,0 单元,7,5,1,1,0,1,1,0 单元,8,6,1,1,0,1,1,0 单元,3,8,1,1,0,1,1,0 单元,8,7,1,1,0,1,1,0 结点支承,1,2,-90,0,0 结点支承,4,1,0,0 END 观览器中显示的图形如图 2-5-1a 所示。然后,在编辑器中依次选菜单“求解”、“几何 组成”,得到“有多余约束的几何瞬变体系”的结论。在“几何构造分析”对话框中选“动 态显示”,则可在观览器中看到机构运动模态的动画显示,如图 2-5-1b 所示。 其次,考虑智能求解。在编辑器中依次选菜单“求解”、“几何构造”,在弹出的对话 框中单击“计算”按钮,得到如下的结果: 不必考虑大地及其支座 刚片 1 由以下杆件构成:(4) (5) (6) 将刚片 1 看成第一个刚片 将杆件 (7) 看成第二个刚片 将杆件 (10) 看成第三个刚片 由三刚片规则,连接三刚片的三个(虚)铰过一直线,瞬变体系 讨论: 对本题,手解时有两种思路,一种如上所示,另一种则仍将杆件(4)、(5)、(6)看成刚片 1 (第一个刚片),而将杆件(2)和(11)分别看成第二、三个刚片。在第二种思路中,其中的一个 瞬铰的位置可以在结点 1 和 4 的连线的任一点,很难将常规的三刚片法则准确应用,因此不 宜采用。求解器的智能求解算法考虑到这种情况,没有采用第二种思路,因而给出了正确的 计算步骤和结果。 例 2-5-2 使用求解器分析图 2-5-2 所示的几何构造。 图2-5-2 例2-5-2图 2