
解法三:此题也可根据网络结构的特点,令各支路电流如图(3)所示,则左上角的 网孔回路方程为 2B2=2R, 故 2= 由结点①的KCL方程 0.5i=2+i1=22=21 得 4== 由此得端口电压4=R×0.5i+2R×i+R×0.5i=号R 所以 R=告=R=3Q R (e3) (f)图中(12,12,22)和(22,22,12)构成两个Y形连接,分别将两个Y形转化成等 值的△形连接,如图(f1)和(f2)所示。 等值△形的电阻分别为 R=1+1+1)=2.50 R=1+2+1×2)=52 R=R=52 R=2+2+2x2=80 5=1+2+1×2=42 R=R=42 并接两个△形,最后得图(3)所示的等效电路,所以 R=[2IlR∥R)+R∥R]IR∥R) =[25∥4)+2.518]5∥4) -[20,4020-1269n 19+2i"9
解法三:此题也可根据网络结构的特点,令各支路电流如图(e3)所示,则左上角的 网孔回路方程为 2Ri2 = 2Ri1 故 2 1 i = i 由结点①的 KCL 方程 5 2 1 2 2 2 1 0. i = i + i = i = i 得 i i i 4 1 2 = 1 = 由此得端口电压 u R i R i R i Ri ab 2 3 0.5 4 1 = 0.5 + 2 + = 所以 = = = 3 2 3 R i u R ab ab (f)图中 (1 ,1 , 2 ) 和 (2 , 2 ,1 ) 构成两个 Y 形连接,分别将两个 Y 形转化成等 值的△形连接,如图(f1)和(f2)所示。 等值△形的电阻分别为 = = = = + + = = = = + + = = = + + = + + 4 4 2 1 2 1 2 8 1 2 2 5 2 2 ) 5 1 1 2 ) 2.5 (1 2 2 1 1 (1 1 2 3 2 3 2 1 1 2 R R R R R R R R 并接两个 形,最后得图(f3)所示的等效电路,所以 2 2 1 1 3 3 2 //( // ) // //( // ) 2 //(5// 4) 2.5// 8 //(5// 4) 20 40 20 // 1.269 19 21 9 R R R R R R R ab = + = + = + =
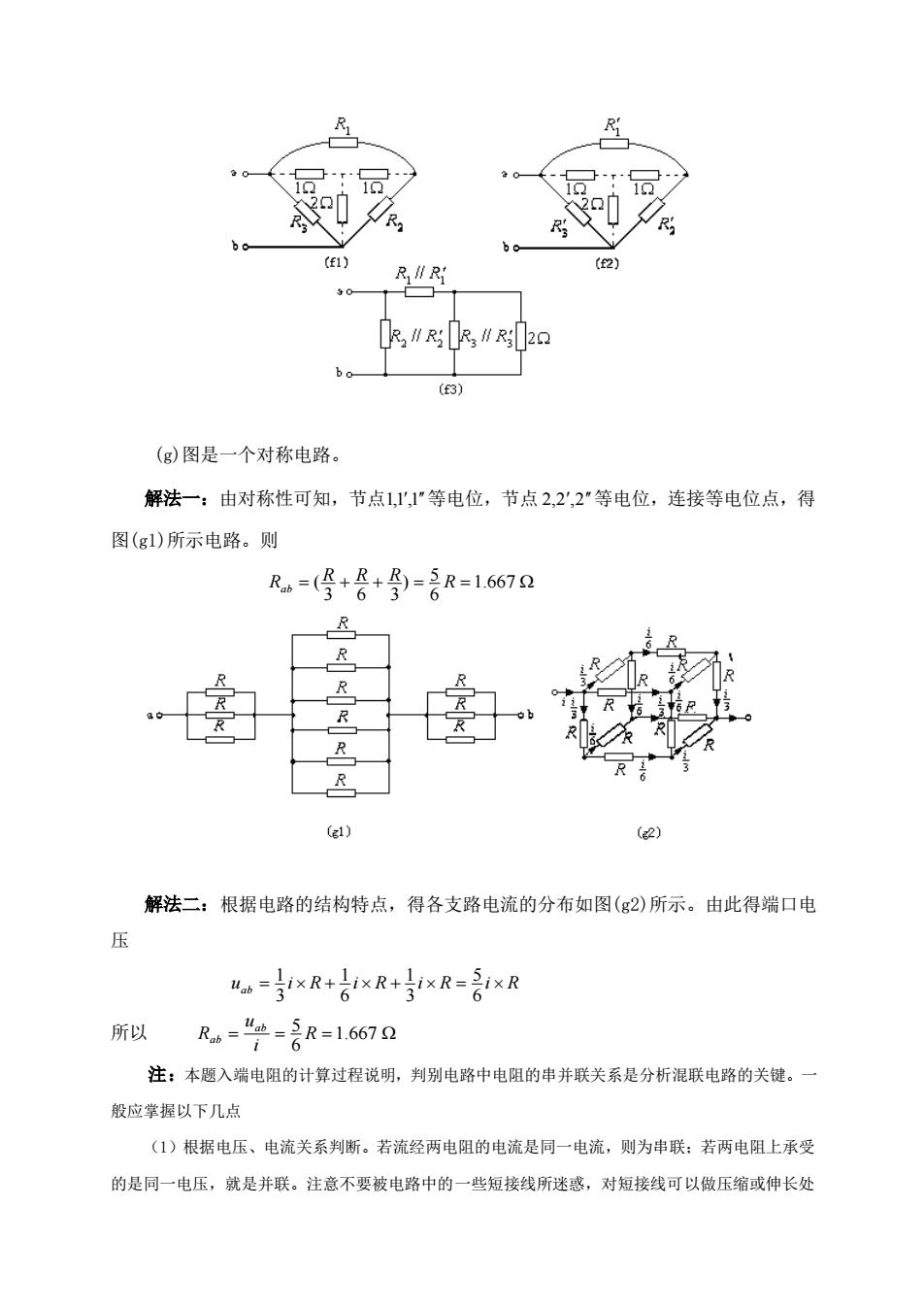
R∥RR∥R2Q (3) (g)图是一个对称电路。 解法一:由对称性可知,节点1,1"等电位,节点2,2,2“等电位,连接等电位点,得 图(g1)所示电路。则 Rb=(号+8+)=2R=1.6672 e4) (e2) 解法二:根据电路的结构特点,得各支路电流的分布如图(g2)所示。由此得端口电 压 s=}×R+名×R+ixR=名xR 所以Rs=-名R=1.67Q 注:本题入端电阻的计算过程说明,判别电路中电阻的串并联关系是分析混联电路的关键。一 般应掌握以下几点 (1)根据电压、电流关系判断。若流经两电阻的电流是同一电流,则为串联:若两电阻上承受 的是同一电压,就是并联。注意不要被电路中的一些短接线所迷惑,对短接线可以做压缩或伸长处
(g)图是一个对称电路。 解法一:由对称性可知,节点 1,1 ,1 等电位,节点 2,2 ,2 等电位,连接等电位点,得 图(g1)所示电路。则 = + + = = 1.667 6 5 ) 3 6 3 ( R R R R Rab 解法二:根据电路的结构特点,得各支路电流的分布如图(g2)所示。由此得端口电 压 uab = i R + i R + i R = i R 6 5 3 1 6 1 3 1 所以 = = = 1.667 6 5 R i u R ab ab 注:本题入端电阻的计算过程说明,判别电路中电阻的串并联关系是分析混联电路的关键。一 般应掌握以下几点 (1)根据电压、电流关系判断。若流经两电阻的电流是同一电流,则为串联;若两电阻上承受 的是同一电压,就是并联。注意不要被电路中的一些短接线所迷惑,对短接线可以做压缩或伸长处