
记 收敛性与连续故 收敛性与连续性 例 对每个KCC2,定义PK:C(2)→R为PK()=supxEKIf(x)I: 则PK是C(2)上的一个半范.另外,pn是C(①)上的一个范数. 对每个j,0≤j≤k,及KCC2通过 Pk()=sup{Def(x):x∈K,lal≤}可定义C*(2)上的一个半 范.每个这样的P?都是C*(①)上的一个范数. 1口10元11无克月00 实芳芳 Sobolev空傅 一满助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 例 对每个 K ⊂⊂ Ω, 定义 pK : C(Ω) → R 为 pK(f) = supx∈K |f(x)|. 则 pK 是 C(Ω) 上的一个半范. 另外,pΩ 是 C(Ω) ¯ 上的一个范数. 对每个 j, 0 ≤ j ≤ k, 及 K ⊂⊂ Ω 通过 pj,K(f) = sup{|D αf(x)| : x ∈ K, |α| ≤ j} 可定义 C k (Ω) 上的一个半 范. 每个这样的 pj,Ω 都是 C k (Ω) 上的一个范数. 窦芳芳 Sobolev 空间 ——辅助知识

记 收敛性与连续故 收敛性与连续性 定义 如果1imp(vk-)=0,则称V中序列{vk}1在v∈V中关 于p收敛 记为在(V,p)中Vn→V,当不致混淆时省略p 1口卡4回子1元电月风0 实芳芳 Sobolev空博 一满助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 定义 如果 lim k→∞ p(vk − v) = 0,则称 V 中序列 {vk} ∞ k=1 在 v ∈ V 中关 于 p 收敛. 记为在 (V, p) 中 vn → v,当不致混淆时省略 p. 设 S ⊂ V. S 的闭包在 (V, p) 中是集合 ¯S = {v ∈ V : 对某些S 中的序列{vn} ∞ n=1 , vn → v in (V, p)}. 如果 S = ¯S,S 称为闭的. S 的闭包 ¯S 是包含 {S : S ⊂ ¯S} 的 最小闭集, ¯S = ¯¯S, 如果 S ⊂ K = K¯ 则 ¯S ⊂ K. 窦芳芳 Sobolev 空间 ——辅助知识

记明 收敛性与连续战 收敛性与连续性 定义 如果1imp(vk-)=0,则称V中序列{vk}1在v∈V中关 于p收敛 记为在(V,p)中Vn→V,当不致混淆时省略p. 设SCV.S的闭包在(V,p)中是集合 5={v∈V:对某些S中的序列{n}e1n→vin(V,p) 4口卡4021元电月只0 实芳芳 Sobolev空博 一蒲助知识
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 定义 如果 lim k→∞ p(vk − v) = 0,则称 V 中序列 {vk} ∞ k=1 在 v ∈ V 中关 于 p 收敛. 记为在 (V, p) 中 vn → v,当不致混淆时省略 p. 设 S ⊂ V. S 的闭包在 (V, p) 中是集合 ¯S = {v ∈ V : 对某些S 中的序列{vn} ∞ n=1, vn → v in (V, p)}. 如果 S = ¯S,S 称为闭的. S 的闭包 ¯S 是包含 {S : S ⊂ ¯S} 的 最小闭集, ¯S = ¯¯S, 如果 S ⊂ K = K¯ 则 ¯S ⊂ K. 窦芳芳 Sobolev 空间 ——辅助知识
记明 收敛性与连续故 收敛性与连续性 定义 如果1imp(vk-)=0,则称V中序列{vk}1在v∈V中关 于p收敛 记为在(V,p)中n→V,当不致混淆时省略P. 设SCV.S的闭包在(V,p)中是集合 5={v∈V:对某些S中的序列{vn}e1,n→vin(V,p)} 如果S=5,5称为闭的.S的闭包5是包含{5:5C5}的 最小闭集,5=5,如果SCK=衣则5CK 口卡4回于1元克月只0 实芳芳 Sobolev空博 一蒲助知识
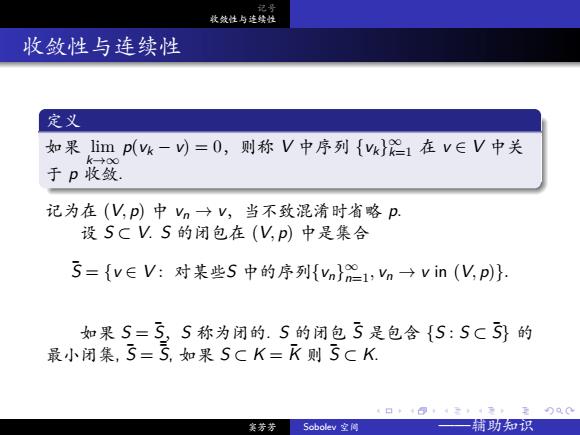
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 记号 收敛性与连续性 收敛性与连续性 定义 如果 lim k→∞ p(vk − v) = 0,则称 V 中序列 {vk} ∞ k=1 在 v ∈ V 中关 于 p 收敛. 记为在 (V, p) 中 vn → v,当不致混淆时省略 p. 设 S ⊂ V. S 的闭包在 (V, p) 中是集合 ¯S = {v ∈ V : 对某些S 中的序列{vn} ∞ n=1, vn → v in (V, p)}. 如果 S = ¯S,S 称为闭的. S 的闭包 ¯S 是包含 {S : S ⊂ ¯S} 的 最小闭集, ¯S = ¯¯S, 如果 S ⊂ K = K¯ 则 ¯S ⊂ K. 窦芳芳 Sobolev 空间 ——辅助知识