第十九章教学基本要求 第十九章振动 2元 x一t图 角频率0=2πV= 2π秒内的振动次数。 (单位:1/S或rad/S) O,T,V都表示简谐运动的周期性,反映振动的快慢
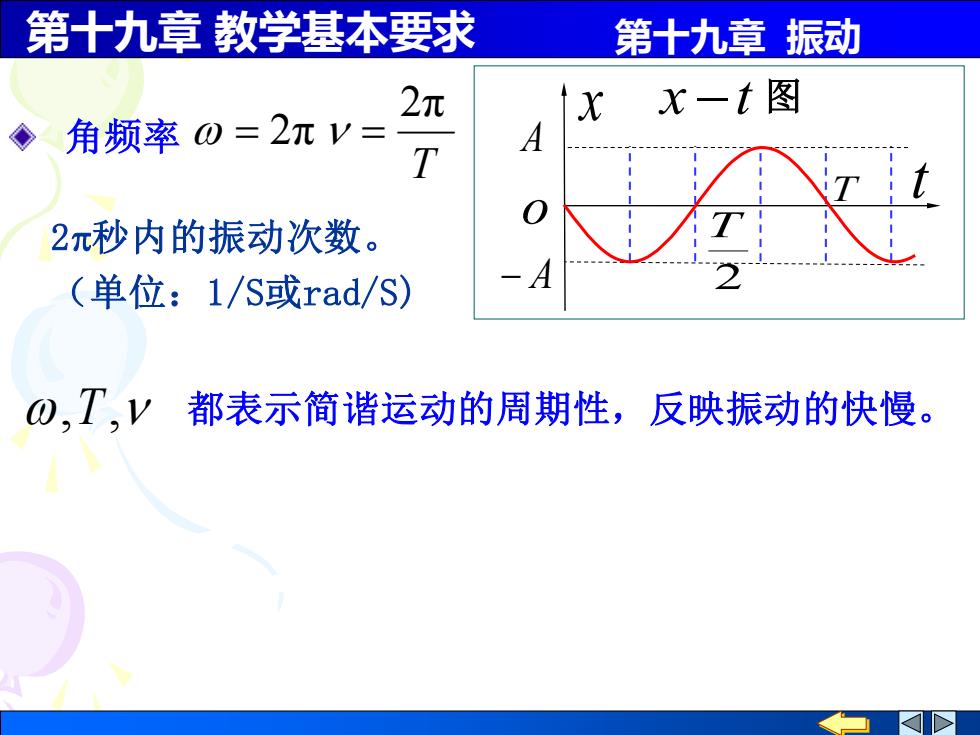
第十九章 教学基本要求 第十九章 振动 T 2π 角频率 = 2π = x −t 图 A − A x T 2 T t o ,T, 都表示简谐运动的周期性,反映振动的快慢。 2秒内的振动次数。 (单位:1/S或rad/S)

第十九章教学基本要求 第十九章振动 >相位 在x=Ac0s(ot+p)中,ot+p 称为振动的相位。 1)wt+D>x,存在一一对应的关系;即其决定 质点在时刻的t的位置。 2)相位在0~2元内变化,质点无相同的运动状态; 相差2n元(为整数)质点运动状态全同.(周期性) 3) 初相位0(t=0) 描述质点初始时刻的运动状态, (0取[-元>元或[0>2元)
第十九章 教学基本要求 第十九章 振动 1) ,存在一一对应的关系;即其决定 质点在时刻的t的位置。 t + → x 2)相位在 0 ~ 2π 内变化,质点无相同的运动状态; ➢相位 3)初相位 (t = 0) 描述质点初始时刻的运动状态. 相差 2nπ (n 为整数 ) 质点运动状态全同.(周期性) ( 取 [−π →π] 或 [0→2π] ) 在 x = Acos(t +) 中, t + 称为振动的相位
第十九章教学基本要求 第十九章振动 t时刻的相位反映t时刻的振动状态(x、D、a) 由x=Acos(ot+p) wt +o 元/2 元 3元/2 2元 x(t) A 0 -A 0 A (t) 0 -0A 0 @A 0 a(t) -aPA 0 aA 0 -aPA
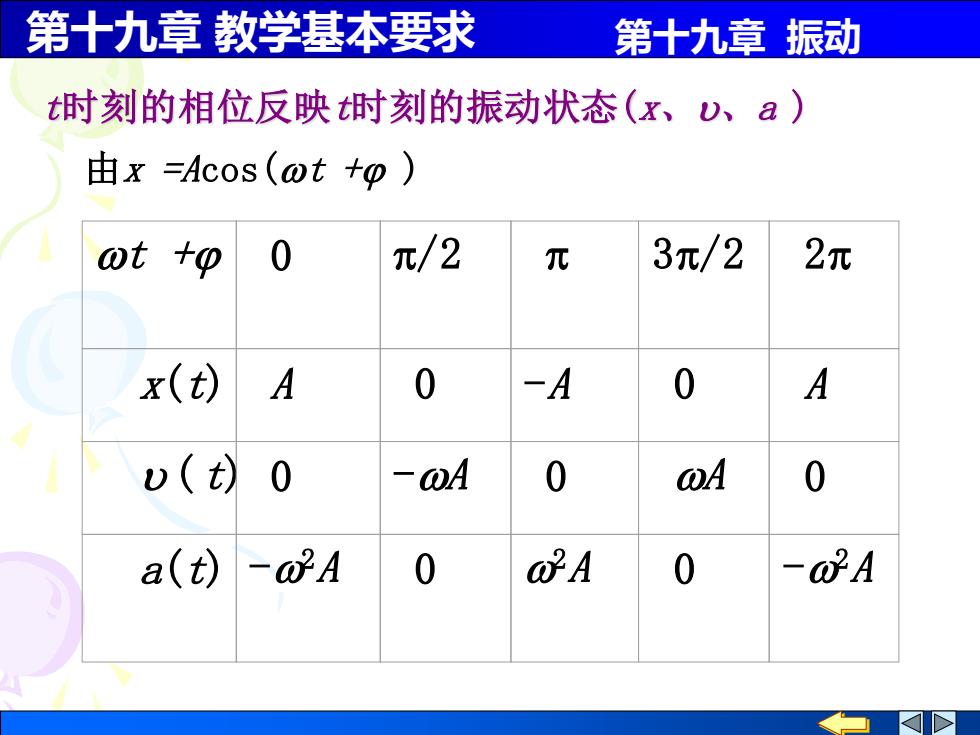
第十九章 教学基本要求 第十九章 振动 t时刻的相位反映t时刻的振动状态(x、、a ) 由x =Acos(t + ) t + 0 /2 3/2 2 x(t) A 0 -A 0 A ( t) 0 -A 0 A 0 a(t) -2A 0 2A 0 -2A
第十九章教学基本要求 第十九章振动 弹簧振子的几个特殊的初始状态及相应的振动曲线 π/2 元 3π/2 2元 Xo A 0 -A 0 A 0 -0A 0 @A 0
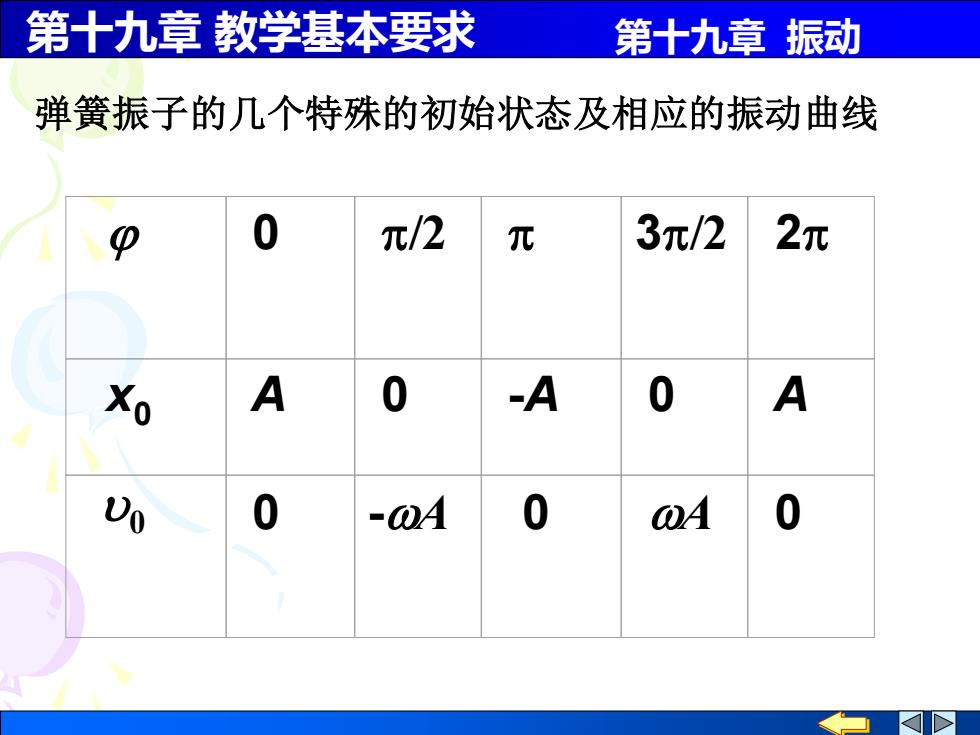
第十九章 教学基本要求 第十九章 振动 弹簧振子的几个特殊的初始状态及相应的振动曲线 0 0 /2 3/2 2 x0 A 0 -A 0 A 0 -A 0 A 0
第十九章教学基本要求 第十九章振动 0 m (a) w T π/2 (b) x0=0
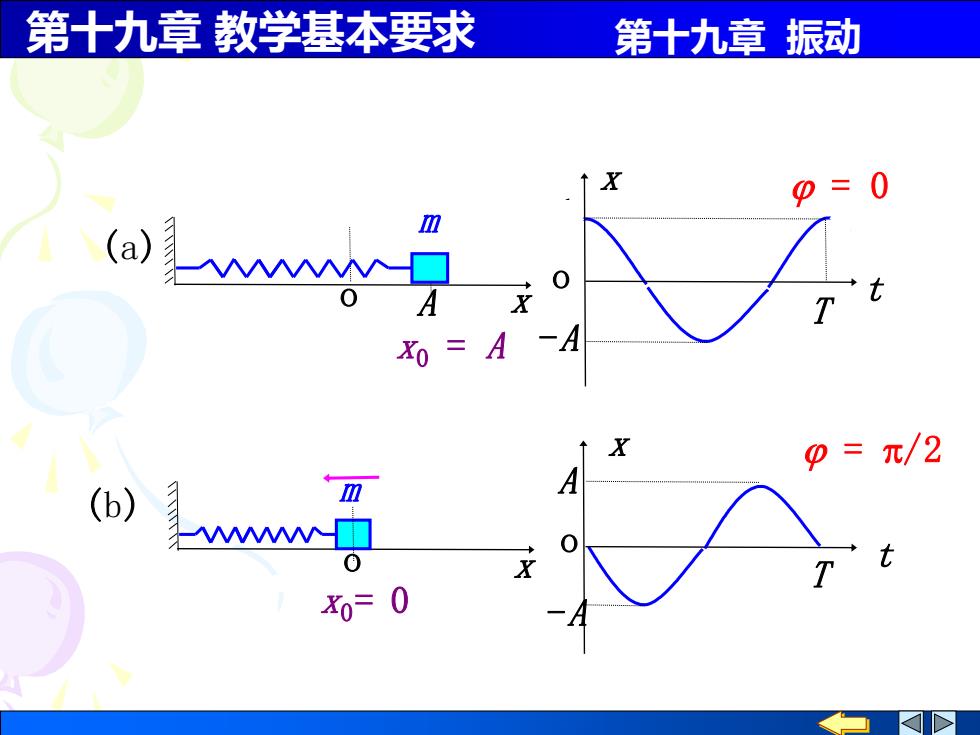
第十九章 教学基本要求 第十九章 振动 o A -A t x = 0 T (a) A x0 = A x m o o A -A t x = /2 x0= 0 T (b) x m o