
第5章列则体运动学 刚体运动随处可见,观览轮盘是一种具有水平转轴、能在铅垂平面内 回转的装置。轮盘和吊箱的运动各有什么样的特点?如何描述?
第5章 刚体运动学 刚体运动随处可见,观览轮盘是一种具有水平转轴、能在铅垂平面内 回转的装置。轮盘和吊箱的运动各有什么样的特点?如何描述?
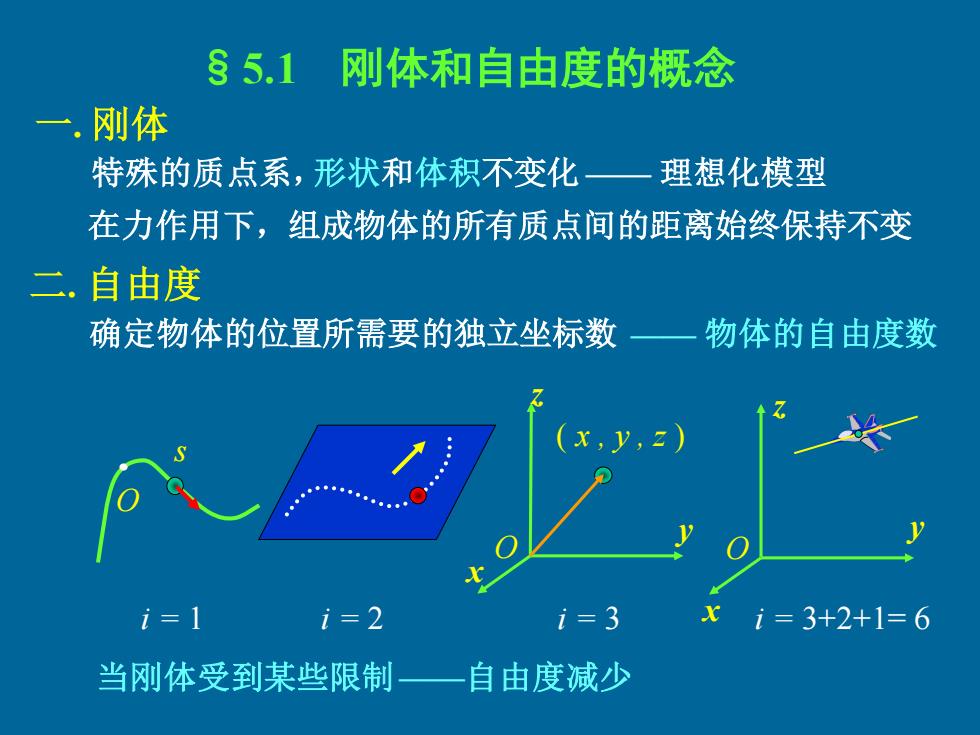
§5.1 刚体和自由度的概念 刚体 特殊的质点系,形状和体积不变化一理想化模型 在力作用下,组成物体的所有质点间的距离始终保持不变 二,自由度 确定物体的位置所需要的独立坐标数一 物体的自由度数 i=1 i=2 i=3 i=3+2+1=6 当刚体受到某些限制 自由度减少
§5.1 刚体和自由度的概念 一. 刚体 特殊的质点系,形状和体积不变化 —— 理想化模型 在力作用下,组成物体的所有质点间的距离始终保持不变 二. 自由度 确定物体的位置所需要的独立坐标数 —— 物体的自由度数 s O i = 1 x y z O ( x , y , z ) i = 2 i = 3 x y z O i = 3+2+1= 6 当刚体受到某些限制——自由度减少
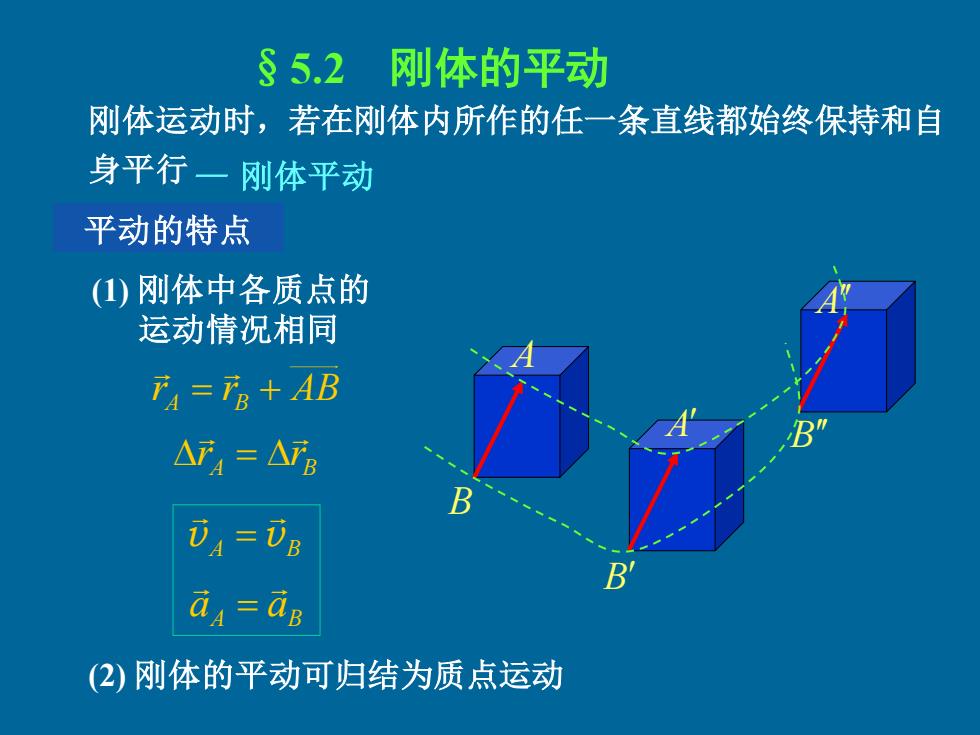
§5.2刚体的平动 刚体运动时,若在刚体内所作的任一条直线都始终保持和自 身平行 一刚体平动 平动的特点 (1)刚体中各质点的 运动情况相同 4=3+AB △7产=△WB i4=0。 B (2)刚体的平动可归结为质点运动
§5.2 刚体的平动 刚体运动时,若在刚体内所作的任一条直线都始终保持和自 身平行— 刚体平动 A B A B A B 平动的特点 (1) 刚体中各质点的 运动情况相同 rA = rB + AB A B r r = v A vB = A B a a = (2) 刚体的平动可归结为质点运动
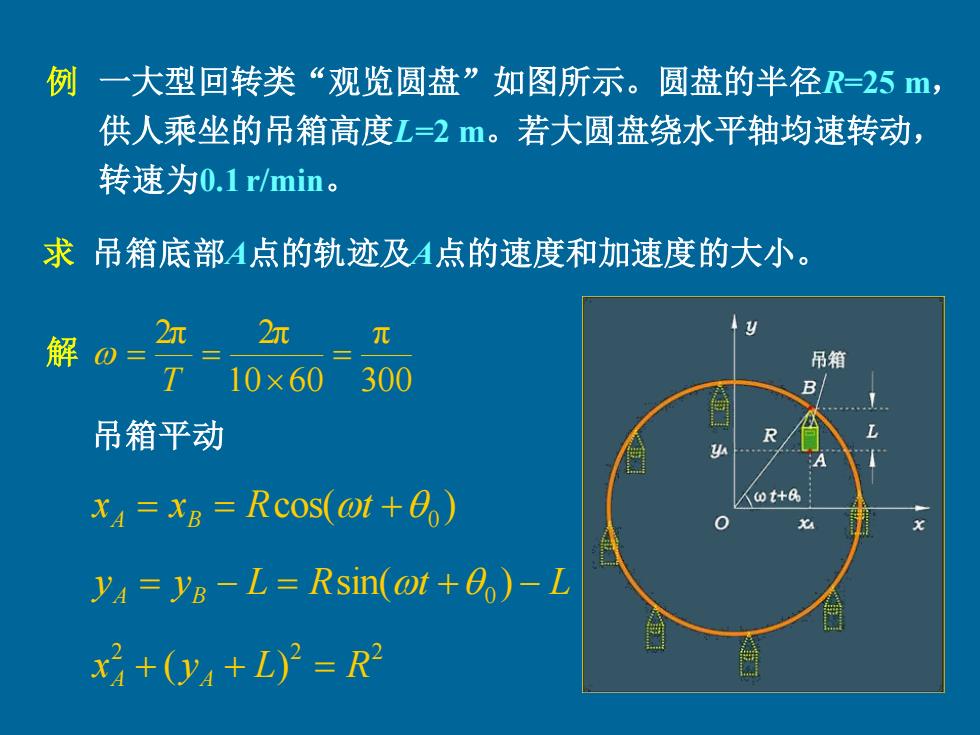
例 一大型回转类“观览圆盘”如图所示。圆盘的半径R=25, 供人乘坐的吊箱高度L=2。若大圆盘绕水平轴均速转动, 转速为0.1r/min。 求吊箱底部4点的轨迹及4点的速度和加速度的大小。 解0= 2n 2n 元 吊箱 T 10×60 300 吊箱平动 R X=xB=Rcos(@t+00) 人0t+A 0 ya=y8-L=Rsin(@t+)-L x+(y4+L)2=R
一大型回转类“观览圆盘”如图所示。圆盘的半径R=25 m, 供人乘坐的吊箱高度L=2 m。若大圆盘绕水平轴均速转动, 转速为0.1 r/min。 例 300 π 10 60 2π 2π = = = T cos( ) = = + 0 x x R t A B yA = yB − L = Rsin(t + 0 ) − L 2 2 2 xA + ( yA + L) = R 解 求 吊箱底部A点的轨迹及A点的速度和加速度的大小。 吊箱平动
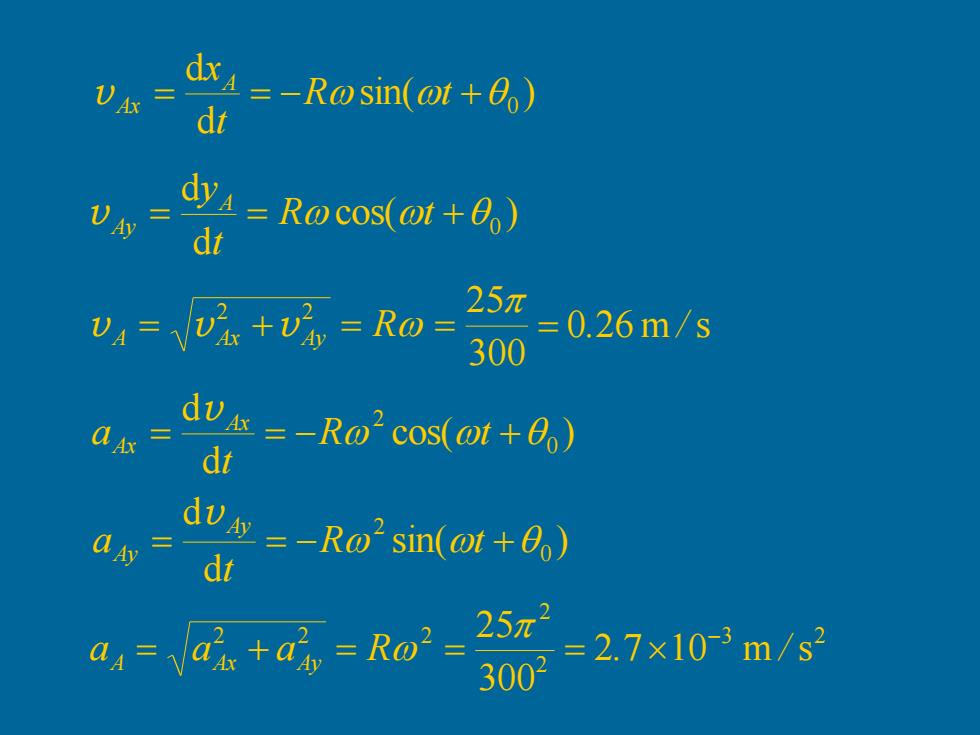
drA=-Rwsin(ot+B,) dt dyi=Rocos(ot+0) dt Va=v'is +vily Ro= 25 =0.26m/s 300 dv=-Ro2cos(OI+0o) dt a Ay dv=-Ro2sim(ot+8,) dt 7+a6=Ro2=-25x2 3002 =2.7×10-3m/s
300 2 2 25 v A = v Ax +v Ay = R = = 0.26 m / s cos( ) d d 0 2 = = −R t + t a Ax Ax v 3 2 2 2 2 2 2 2 7 10 m s 300 25 a a a R . / A Ax Ay − = + = = = sin( ) d d 0 2 = = −R t + t a Ay Ay v sin( ) d d = = − + 0 R t t xA v Ax cos( ) d d = = + 0 R t t yA v Ay