
第四篇电磁学 第九章真空中的静电场 §9-1,2概述 一、电荷与电场 1.电荷:实物的一种属性。 三个基本性质: ①自然界存在两种电荷:正电荷和负电荷 ②电荷守恒 ③电荷的量子化(微观世界的一个基本定律) 最小电量:1.602×10-19库仑 点电荷:不考虑大小和分布状况而可看作集中于一点的电荷。 ①实际有许多情况可以近似成点电荷。 ②点电荷的位置可以方便地在坐标上标出。 电荷守恒定律: 在一个与外界没有电荷交换的系统内,在任一时刻存在于系统中的 正电荷与负电荷的代数和始终保持不变。 ①强调是正负电荷的代数和不变。 ②电荷守恒定律是物理学的基本定律之一。 2.电场 直观上看,电场是给电荷以作用力的物理场。若空间某一区域内各 点具有给予在该点的静止电荷的作用力的属性,就说该区域存在着电场。 电荷一场一电荷 从本质上说:电场是物质的一种存在形式,具有能量、动量和质量。 本章只讨论相对于观察者静止的电荷在其周围空间产生的电场即静电场。 二、库仑定律(实验定律:1785年;电磁学从定性到定量的重要里程碑) 表示两个相对静止的点电荷之间的相互作用的定律,是静电学的基础
第四篇 电磁学 第九章 真空中的静电场 §9-1,2 概述 一、电荷与电场 1.电荷:实物的一种属性。 三个基本性质: ① 自然界存在两种电荷:正电荷和负电荷 ② 电荷守恒 ③ 电荷的量子化(微观世界的一个基本定律) 最小电量: 19 1.602 10− 库仑 点电荷:不考虑大小和分布状况而可看作集中于一点的电荷。 ① 实际有许多情况可以近似成点电荷。 ② 点电荷的位置可以方便地在坐标上标出。 电荷守恒定律: 在一个与外界没有电荷交换的系统内,在任一时刻存在于系统中的 正电荷与负电荷的代数和始终保持不变。 ① 强调是正负电荷的代数和不变。 ② 电荷守恒定律是物理学的基本定律之一。 2. 电场 直观上看,电场是给电荷以作用力的物理场。若空间某一区域内各 点具有给予在该点的静止电荷的作用力的属性,就说该区域存在着电场。 电荷 场 电荷 从本质上说:电场是物质的一种存在形式,具有能量、动量和质量。 本章只讨论相对于观察者静止的电荷在其周围空间产生的电场即静电场。 二、库仑定律(实验定律;1785 年;电磁学从定性到定量的重要里程碑) 表示两个相对静止的点电荷之间的相互作用的定律,是静电学的基础

=l=k84✉;方=-元=k94正=k94元 r ri2ri2 2 7429万 →⊕→ ←⊙ 注意: ①国际单位制[S]中,k=8.988×10N·m2.c2, 而电磁学部分MKSA有理制中 ,;6-8.85×10-12C2.N-m2 1494。 方无装轻病号 ②满足“平方反比律”,这种力称为“库仑力”或“静电力” ③两静止电荷之间的静电力虽然满足大小相等,方向相反,作用在一条 直线上,但不是一对作用力与反作用力。 例题9-1:在氢原子内,电子和原子核之间的距离为r=0.529×10-0m。试计算电子和 原子核之间的静电作用力和万有引力并比较两者大小。又设原子核中的两质子相距 5=4.0×10-5m,求此两质子之间的静电力。 解:已知m。=9.11x10-kg,M氯楼=1.67×10kg 9,=42=1.6×10-9C,G。=6.67x10-1"Nm2.kg2 94=900x10°×06x10-2 人.=46了 (0.529x100y-823x10-*N f=GAm=66x101T×6Zx10-27 -=3.64×10-47N (0.529×10-10)y2 会-2i045=5g-90860号=1w
2 12 1 2 12 21 r q q f = f = k ; 3 12 12 1 2 12 12 2 12 1 2 21 12 r r q q k r r r q q f f k = − = = 12 f 1 q 12 r 2 q 21 f 注意: ① 国际单位制[SI]中, 9 2 2 8.988 10 − k = N m c , 而电磁学部分 MKSA 有理制中 4 0 1 k = ; 12 2 1 2 0 8.85 10− − − = C N m 3 12 12 1 2 12 0 12 2 12 1 2 0 21 12 4 1 4 1 r r q q r r r q q f f = − = = ② 满足“平方反比律”,这种力称为“库仑力”或“静电力” ③ 两静止电荷之间的静电力虽然满足大小相等,方向相反,作用在一条 直线上,但不是一对作用力与反作用力。 例题 9-1:在氢原子内,电子和原子核之间的距离为 r m 10 1 0.529 10− = 。试计算电子和 原子核之间的静电作用力和万有引力并比较两者大小。又设原子核中的两质子相距 r m 15 2 4.0 10− = ,求此两质子之间的静电力。 解:已知 me kg 31 9.11 10− = , M 氢核 = kg 27 1.67 10− q q C 19 1 2 1.6 10− = = , 11 2 2 0 6.67 10− − G = N m k g N r q q f e 8 1 0 2 1 9 2 9 2 1 1 2 0 8.23 10 (0.529 10 ) (1.6 10 ) 9.00 10 4 1 − − − = = = N r Mm f m G 4 7 1 0 2 3 1 2 7 1 1 2 1 0 3.64 10 (0.529 10 ) 9.11 10 1.67 10 6.67 10 − − − − − = = = 39 = 2.2710 m e f f ; N r q q Fe 14 (4.0 10 ) (1.6 10 ) 9 10 4 1 15 2 19 2 9 2 1 1 0 = = = − −

§9-3电场强度 1.电场强度矢量E:E=E ;E单位:牛/仑或伏/米 90 它是定量描写电场中各点性质的物理量,是描写电场性质最基本的物理量。 试探电荷q。应满足: ①体积很小以便确定场中每点的性质。 ②电量很小,不影响原来电场的分布。 2。场强迭加原理(迭加原理是经典电磁学的一条基本原理) 当9置于91:92,9,9.产生的场时,分别受到g,92,9,9 的力为万,万,f;由实验知:了=万+方+.了n 969096 3.场强的计算: (1)点电荷电场中的场强: 源点 90 p场点 0) 原点 真空中: 199 了=46F7
§9-3 电场强度 1.电场强度矢量 E : q0 F E = ; E 单位:牛/仑或伏/米 它是定量描写电场中各点性质的物理量,是描写电场性质最基本的物理量。 试探电荷 0 q 应满足: ① 体积很小以便确定场中每点的性质。 ② 电量很小,不影响原来电场的分布。 2.场强迭加原理(迭加原理是经典电磁学的一条基本原理) 当 0 q 置于 q q q qn , , , , 1 2 3 产生的场时,分别受到 q q q qn , , , , 1 2 3 的力为 n f f f , , , 1 2 ;由实验知: n f f f f = + + 1 2 得: n n E E E q f q f q f q f E = = + ++ = 1 + 2 ++ 0 0 2 0 1 0 3.场强的计算: (1)点电荷电场中的场强: 真空中: r r r qq f 2 0 4 0 1 = ; r r r q E 2 4 0 =

(2)点电荷系电场中的场强 原点 Ux 设真空中有9,92,9.,9n个电荷 4π62 由迭加原理: E=E+E,++瓦-2,9 4π6r (3)任意带电体电场中的场强 影 E-e- 对于线电荷分布,线密度为入 对于面电荷分布,面密度为σ E= 对于体电荷分布,体密度为 E=顶:
(2)点电荷系电场中的场强 设真空中有 q q q qn , , , , 1 2 3 个电荷 1 1 2 0 1 1 1 4 r r r q E = , = 2 2 2 0 2 2 2 4 r r r q E n n n n n r r r q E 2 4 0 = 由迭加原理: = = + ++ = n i i i i i n r r r q E E E E 1 2 0 1 2 4 (3)任意带电体电场中的场强 r r r dq dE 2 4 0 1 = = = r r dq E dE 3 4 0 对于线电荷分布,线密度为 = L r r dl E 3 4 0 1 对于面电荷分布,面密度为 r r dS E S = 3 4 0 1 对于体电荷分布,体密度为 = V r r dV E 3 4 0 1
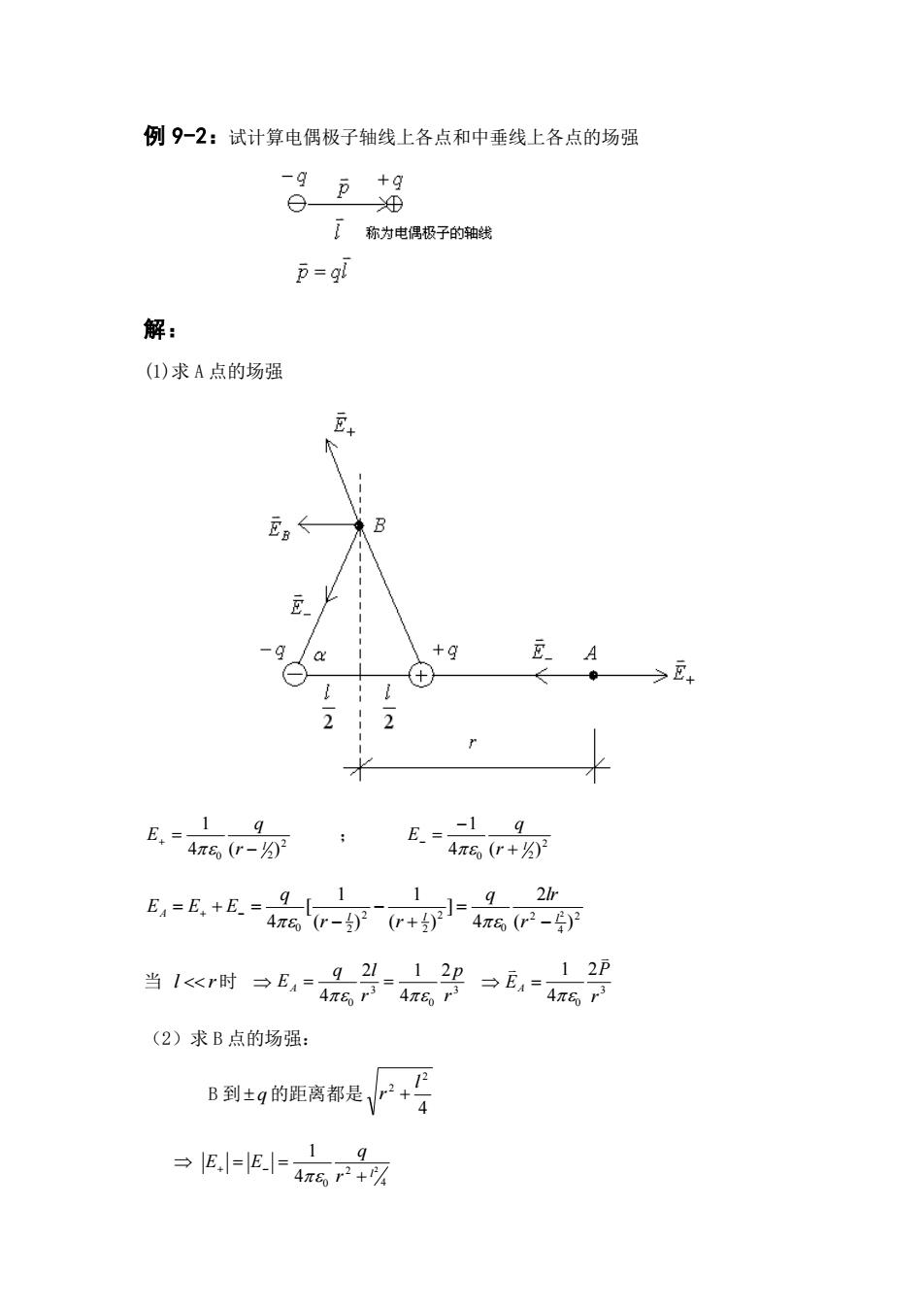
例9-2:试计算电偶极子轴线上各点和中垂线上各点的场强 日月超 了称为电偶极子的轴线 p=gl 解: (I)求A点的场强 2 E.=4+ -1 E,=46-万 (2)求B点的场强: B到的距离都是 →E.=E.4r产+7 9
例 9-2:试计算电偶极子轴线上各点和中垂线上各点的场强 解: (1)求 A 点的场强 2 0 2 4 ( ) 1 l r q E − + = ; 2 0 2 4 ( ) 1 l r q E + − − = 2 4 2 0 2 2 2 0 2 ( ) 2 4 ] ( ) 1 ( ) 1 [ 4 2 l l l A r q lr r r q E E E − = + − − = + + − = 当 l r 时 3 0 3 0 2 4 2 1 4 r p r q l EA = = 3 0 2 4 1 r P EA = (2)求 B 点的场强: B 到 q 的距离都是 4 2 2 l r + 4 2 0 2 4 1 l r q E E + + = − =