
第七章热力学基础 §7-1功热量内能 1、热力学系统和热力学过程 研究关于热现象和热运动规律的物体(组)一一热力学系统 热力学系统的状态随时间的变化一一热力学过程 2、平衡过程(准静态过程) 过程进行的时间大于各状态参量的驰豫时间 例 (1)使系统的温度由T升到2的过程 (2)气体的等温膨胀过程(缓慢提活塞) 若用活塞快速压缩气缸内的气体,则P、V、T都发生变化 3、功热量内能 功和热量是能量交换的二种不同形式(实质) 注意: (1)功和热量是过程的函数(与过程无关),不少态函数 (2)对平衡过程: 便微越)Q=之c- :M_C(T:-T)-MC(T:-T) C是该过程的摩尔热容量 C CM是该过程的比热 Mc是改过程的热容量 对等温过程,C=0,不能用上式计算 对外做功: A-∫dA=PaV 平衡过程在PV图上可以用一条曲线表示。该曲线与V轴所围的面积代表功
第七章 热力学基础 §7-1 功 热量 内能 1、热力学系统和热力学过程 研究关于热现象和热运动规律的物体(组)——热力学系统 热力学系统的状态随时间的变化——热力学过程 2、平衡过程(准静态过程) 过程进行的时间大于各状态参量的驰豫时间 例: (1)使系统的温度由 T1 升到 T2 的过程 (2)气体的等温膨胀过程(缓慢提活塞) 若用活塞快速压缩气缸内的气体,则 P、V、T 都发生变化 3、功 热量 内能 功和热量是能量交换的二种不同形式(实质) 注意: (1)功和热量是过程的函数(与过程无关),不少态函数 (2)对平衡过程: (吸热、放热) C(T T ) MC(T T ) M M CdT M M Q 2 1 2 1 mol T T mol 2 1 = − = − = C 是该过程的摩尔热容量 Mmol C c = ,是该过程的比热 Mc 是改过程的热容量 对等温过程, C = ,不能用上式计算。 对外做功: = = 2 1 v v 2 1 A dA PdV 平衡过程在 PV 图上可以用一条曲线表示。该曲线与 V 轴所围的面积代表功

功、热的单位是焦尔或卡。1卡=4.2焦尔,1焦尔=0.24卡 PA f=Ps 图7-1-1气体膨胀做功及其示意图 内能一 (1)物质系统内部状态决定得能量,是态函数: (2)一般要选择一参考态内能,实际中经常讨论得是内能差: (3)对理想气体内能E仅是T的函数。 §7-2热力学第一定律 它是能量转换和守恒定律在涉及到热现象过程中的具体形式。 Q=E2-E+A 对任意热力学过程适用(固、液、气) Q:吸热,E2-E,是内能增量,A是对外做功。 对状态的微小变化过程 dQ=d正+dA=dE+PdV 对于平衡过程 Q=E:-E+心paV 注意:功、热之间的转换不可能是直接的,必须通过物质系统来完成。 §7-3理想气体的等值平衡过程及摩尔热容量
功、热的单位是焦尔或卡。1 卡=4.2 焦尔,1 焦尔=0.24 卡 图 7-1-1 气体膨胀做功及其示意图 内能—— (1)物质系统内部状态决定得能量,是态函数; (2)一般要选择一参考态内能,实际中经常讨论得是内能差; (3)对理想气体内能 E 仅是 T 的函数。 §7-2 热力学第一定律 它是能量转换和守恒定律在涉及到热现象过程中的具体形式。 Q = E2 − E1 + A 对任意热力学过程适用(固、液、气) Q:吸热, E2 − E1 是内能增量,A 是对外做功。 对状态的微小变化过程 dQ = dE + dA = dE + PdV 对于平衡过程 = − + 2 1 V V Q E2 E1 PdV 注意:功、热之间的转换不可能是直接的,必须通过物质系统来完成。 §7-3 理想气体的等值平衡过程及摩尔热容量 f = Ps dL P O V1 V2 V Ⅰ Ⅱ dV P
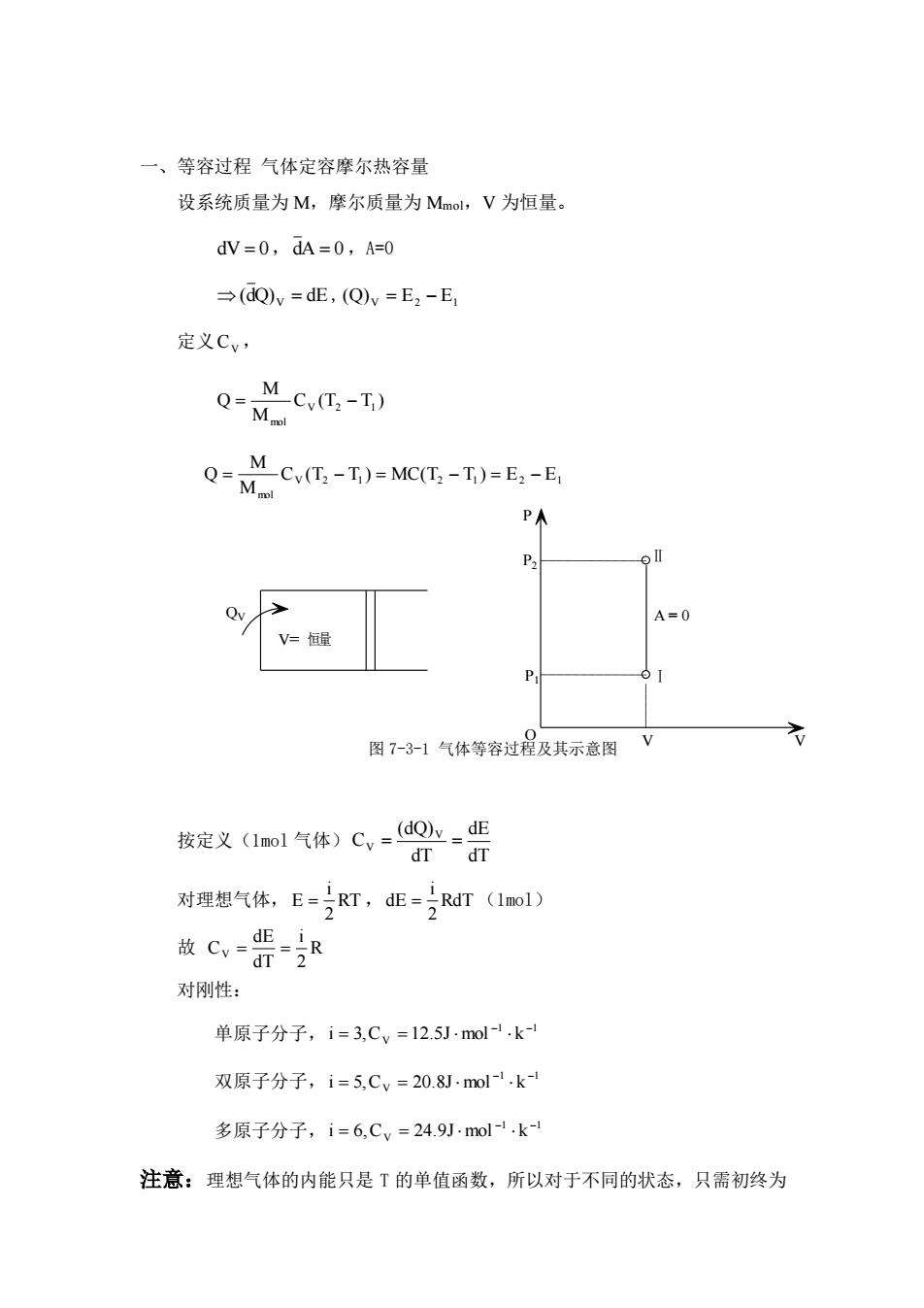
一、等容过程气体定容摩尔热容量 设系统质量为M,摩尔质量为Mml,V为恒量。 dV=0,dA=0,A=0 →(dQv=dE,(Q)v=E2-E, 定义Cv, -c.t,-T) Qc-0=c-0=-E PA 图7-3-1气体等容过程及其示意图V 按定义(1no1气体)Cv=do=dE dr dT 对理想气体,E=RT,d正=号RdT(1mol) 放c,普 对刚性: 单原子分子,i=3,Cv=12.5mol-.k- 双原子分子,i=5,Cv=20.8Jmol1.k 多原子分子,i=6,Cy=24.9mol-1.k 注意:理想气体的内能只是T的单值函数,所以对于不同的状态,只需初终为
一、等容过程 气体定容摩尔热容量 设系统质量为 M,摩尔质量为 Mmol,V 为恒量。 dV = 0,dA = 0,A=0 (dQ)V = dE , V E2 E1 (Q) = − 定义 CV , C (T T ) M M Q V 2 1 mol = − V 2 1 2 1 2 1 mol C (T T ) MC(T T ) E E M M Q = − = − = − 图 7-3-1 气体等容过程及其示意图 按定义(1mol 气体) dT dE dT (dQ) C V V = = 对理想气体, RT 2 i E = , RdT 2 i dE = (1mol) 故 R 2 i dT dE CV = = 对刚性: 单原子分子, 1 1 i 3,CV 12.5J mol k − − = = 双原子分子, 1 1 i 5,CV 20.8J mol k − − = = 多原子分子, 1 1 i 6,CV 24.9J mol k − − = = 注意:理想气体的内能只是 T 的单值函数,所以对于不同的状态,只需初终为 V= 恒量 QV P2 P1 P O V V A = 0 Ⅱ Ⅰ
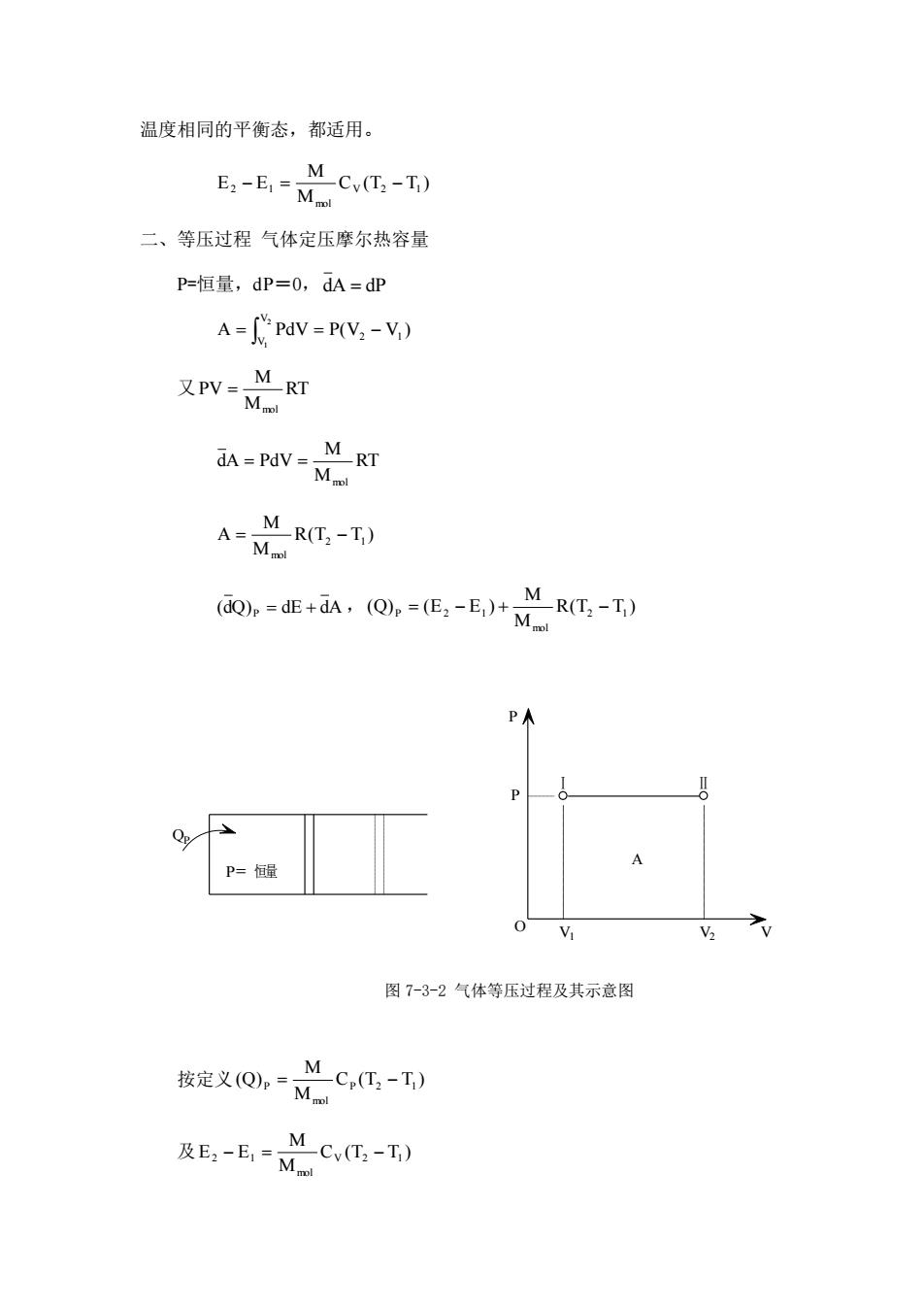
温度相同的平衡态,都适用。 -之c- 二、等压过程气体定压摩尔热容量 P=恒量,dP=O,dA=dP A=[PdV P(V2 -V 又w-总 A-) 国=E,@-e-E之-) 图7-3-2气体等压过程及其示意图 _C,(T:-T) 按定义Q,=M _Cv(T-T) 及E,-E=M
温度相同的平衡态,都适用。 C (T T ) M M E E V 2 1 mol 2 − 1 = − 二、等压过程 气体定压摩尔热容量 P=恒量,dP=0,dA = dP A PdV P(V V ) 2 1 V V 2 1 = = − 又 RT M M PV mol = RT M M dA PdV mol = = R(T T ) M M A 2 1 mol = − (dQ) P = dE + dA , R(T T ) M M (Q) (E E ) 2 1 mol P = 2 − 1 + − 图 7-3-2 气体等压过程及其示意图 按定义 C (T T ) M M (Q) P 2 1 mol P = − 及 C (T T ) M M E E V 2 1 mol 2 − 1 = − P= 恒量 QP P P V1 V2 V A Ⅰ Ⅱ O

代入上式 →C,=Cv+R一一迈耶公式 由CRC,片2R 定义v=C.i+2一比热容比 Cy 对刚性: 单原子分子,i=3,C。=20.81Jmol1.k,v=1.67 双原子分子,i=5,Cp=29.1olk,v=1.40 多原子分子,i=6,Cp-33.2小mol.k-,v=1.33 例:一气缸中储有氮气,质量为1.25kg。在标准大气压下缓慢地加热,使 温度升高1K。试求气体膨胀时所作地功A、气体内能的增量△E以及气体所吸 收的热量Q。(活塞的质量以及它与气缸壁的摩擦均可略去。) 解:因过程是等压的,由式 MR(T,-T)得 A=之ar=d品831xU=训 国为-6所以c,-汉-20am,自式正-之c,可后 E之c,A点uw 所以,气体在这一过程中所吸收的热量为 Qp=E2-E,+A=1300J 三、等温过程 T=恒量,dT=0 dE-0,E2-E,=0 (dQ)r=dA,(Q)=A
代入上式 CP = CV + R —— 迈耶公式 由 R 2 i 2 R C 2 i CV P + = = 定义 i i 2 C C V P + = = ——比热容比 对刚性: 单原子分子, i 3,C 20.81J mol k , 1.67 1 1 = P = = − − 双原子分子, i 5,C 29.11J mol k , 1.40 1 1 = P = = − − 多原子分子, i 6,C 33.21J mol k , 1.33 1 1 = P = = − − 例:一气缸中储有氮气,质量为 1.25kg。在标准大气压下缓慢地加热,使 温度升高 1K。试求气体膨胀时所作地功 A、气体内能的增量 E 以及气体所吸 收的热量 QP。(活塞的质量以及它与气缸壁的摩擦均可略去。) 解:因过程是等压的,由式 R(T T ) M M RdT M M A 2 1 mol T T mol 2 1 = = − 得 8.31 1J 371J 0.028 1.25 R T M M A mol = = = 因为 i=5,所以 R 20.8J/(mol K) 2 i CV = = 。由式 C dT M M dE V mol = 可得, 20.8 1J 929J 0.028 1.25 C T M M E V mol = = = 所以,气体在这一过程中所吸收的热量为 Q E E A 1300J P = 2 − 1 + = 三、等温过程 T=恒量,dT=0 dE=0,E2 − E1 = 0 (dQ)T = dA,(Q)T = A