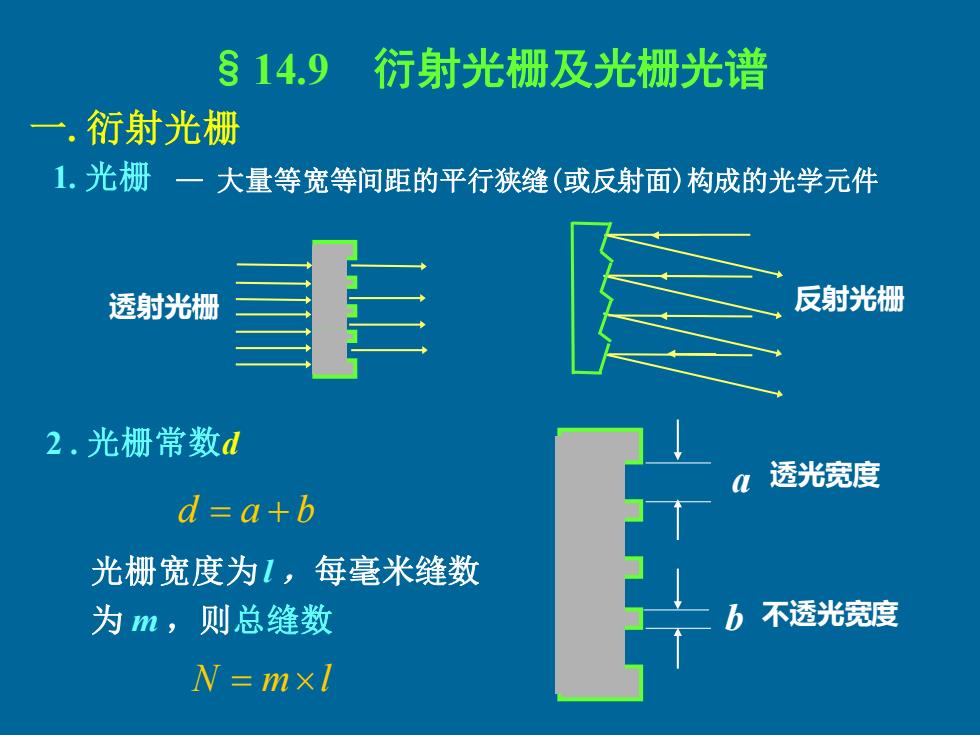
§14.9 衍射光栅及光栅光谱 一.衍射光栅 1.光栅 一大量等宽等间距的平行狭缝(或反射面)构成的光学元件 透射光栅 反射光栅 2.光栅常数d 透光宽度 d三a+b 光栅宽度为1,每毫米缝数 为m,则总缝数 不透光宽度 N=mxl
一. 衍射光栅 1. 光栅 透射光栅 反射光栅 透光宽度 不透光宽度 2 . 光栅常数d d = a + b a b — 大量等宽等间距的平行狭缝(或反射面)构成的光学元件 光栅宽度为l ,每毫米缝数 为 m ,则总缝数 N = ml §14.9 衍射光栅及光栅光谱
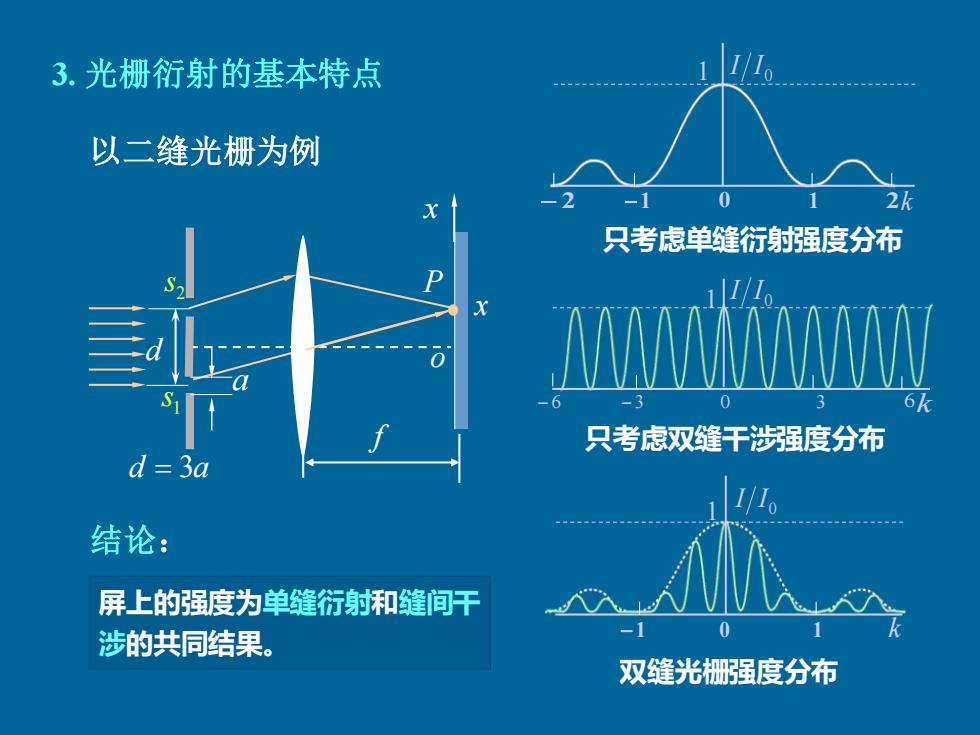
3.光栅衍射的基本特点 以二缝光栅为例 0 X 2k 只考虑单缝衍射强度分布 6 只考虑双缝干涉强度分布 三30 I/1 结论: 屏上的强度为单缝衍射和缝间干 涉的共同结果。 0 双缝光栅强度分布
− 1 0 1 k 1 0 I I − 2 2 x 2 s d P 1 s o a d = 3a 只考虑单缝衍射强度分布 只考虑双缝干涉强度分布 双缝光栅强度分布 f 3. 光栅衍射的基本特点 屏上的强度为单缝衍射和缝间干 涉的共同结果。 • 以二缝光栅为例 x 结论: − 1 0 1 k 1 0 I I − 6 − 3 0 3 6k 0 I I 1
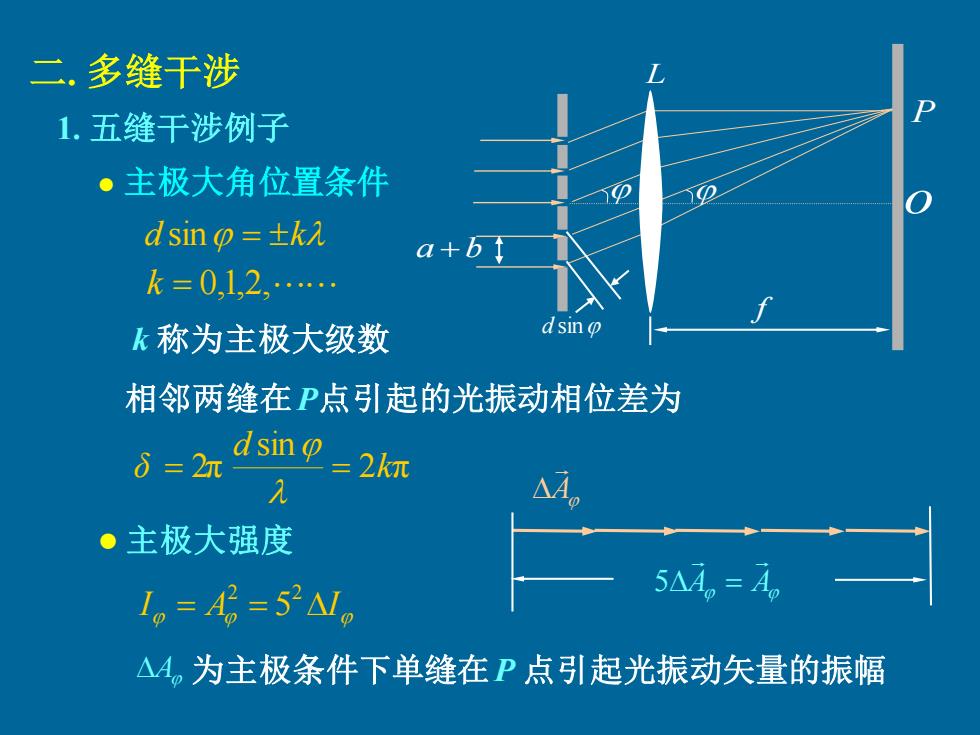
二,多缝干涉 1.五缝干涉例子 。主极大角位置条件 (p dsin o=±k入 a+bt k=01,2,. k称为主极大级数 dsin 相邻两缝在P点引起的光振动相位差为 δ=2r9 sin 2=2kit 入 A ·主极大强度 1。=A6=521。 5AA,A △4。为主极条件下单缝在P点起光振动矢量的振幅
d sin 二. 多缝干涉 1. 五缝干涉例子 d sin = k ⚫ 主极大角位置条件 k = 0,1,2, k 称为主极大级数 2 π sin 2π k d δ = = A A A 5 = I = A = I 2 2 5 相邻两缝在P点引起的光振动相位差为 ⚫ 主极大强度 为主极条件下单缝在P 点引起光振动矢量的振幅 P a + b L f o A
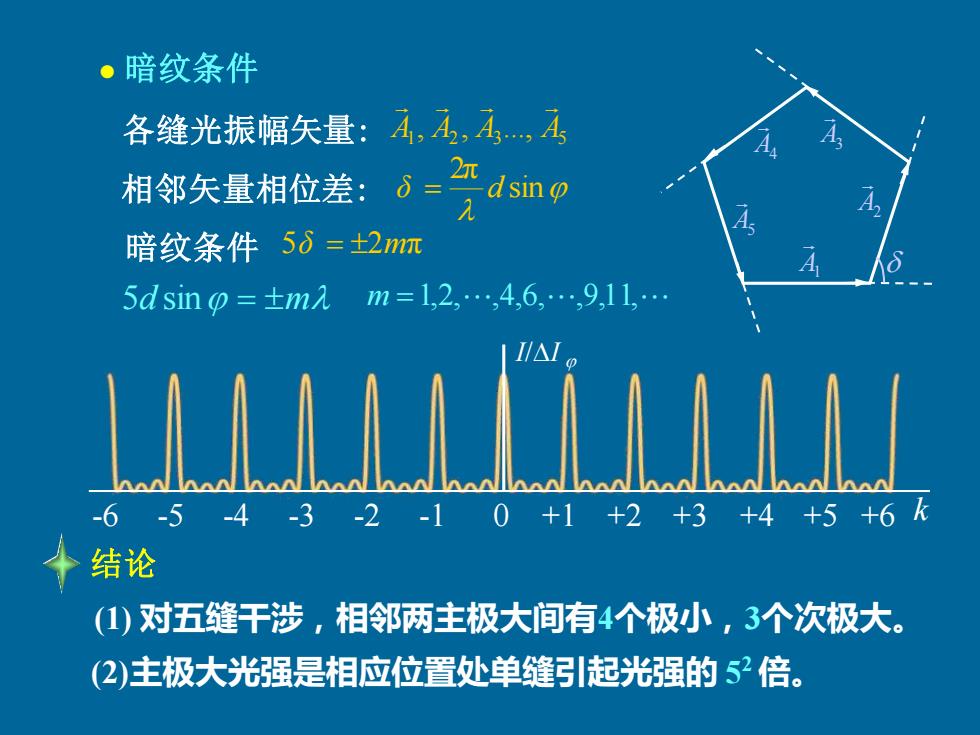
●暗纹条件 各缝光振幅矢量:A,A,A,A 相邻矢量相位差:ò= 沉 dsino 暗纹条件50=+2m 5 dsin o=±m入 m=1,2,4,6,911,. -6-5-4-3-2-10+1+2+3+4+5+6 结论 (1)对五缝干涉,相邻两主极大间有4个极小,3个次极大。 (2)主极大光强是相应位置处单缝引起光强的52倍
5d sin = m m =1,2, ,4,6, ,9,11, 5δ = 2mπ A1 A5 A4 A3 A2 ⚫ 暗纹条件 各缝光振幅矢量: 1 2 3 5 A , A , A ., A 相邻矢量相位差: sin 2π δ = d 暗纹条件 (1) 对五缝干涉,相邻两主极大间有4个极小,3个次极大。 结论 -6 -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 I/I (2)主极大光强是相应位置处单缝引起光强的 5 2 倍。 k
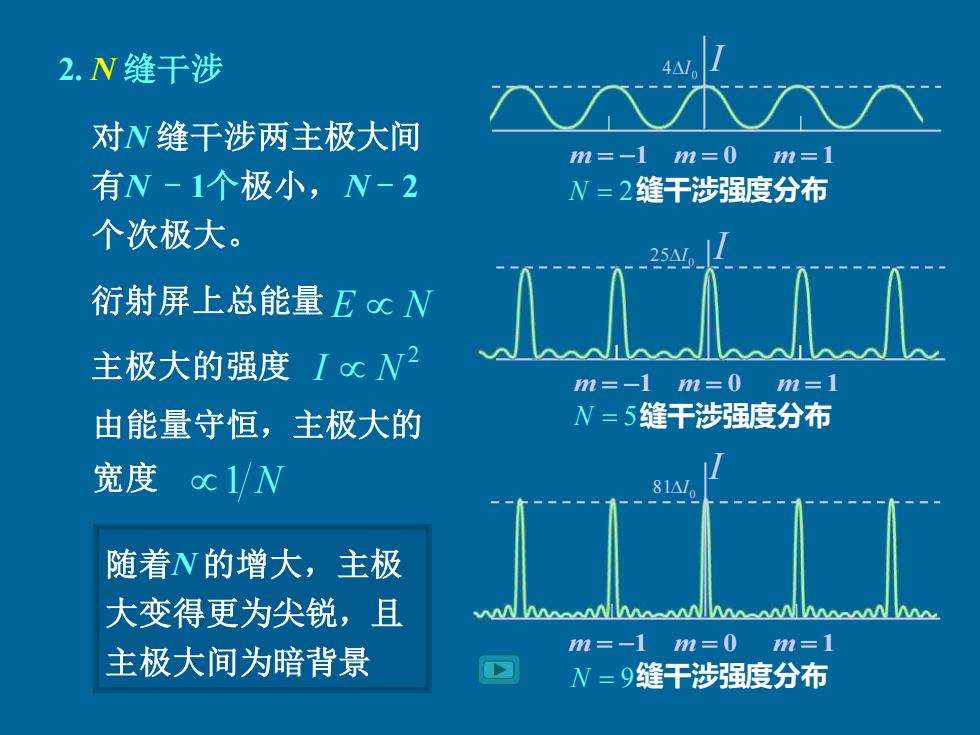
2.N缝干涉 对N缝干涉两主极大间 m=-1m=0m=1 有N-1个极小,N-2 N=2缝干涉强度分布 个次极大。 25△M 衍射屏上总能量EcW 主极大的强度IcW2 m=-1m=0 m=1 由能量守恒,主极大的 N=5缝干涉强度分布 宽度c1/N 81△ 随着N的增大,主极 大变得更为尖锐,且 主极大间为暗背景 m=-1m=0 m=1 N=9缝干涉强度分布
对N 缝干涉两主极大间 有N - 1个极小,N - 2 个次极大。 m = −1 m = 0 m = 1 81 0 I I m = −1 m = 0 m = 1 0 4I I N = 2 N = 5 N = 9 衍射屏上总能量 E N 主极大的强度 2 I N 由能量守恒,主极大的 宽度 1 N 随着N 的增大,主极 大变得更为尖锐,且 主极大间为暗背景 2. N 缝干涉 m = −1 m = 0 m = 1 25 0 I I 缝干涉强度分布 缝干涉强度分布 缝干涉强度分布