广东工业大学：《大学物理》课程教学课件（PPT讲稿）第二十章 波动（20.1-20.10）

例1：已知波函数 y=2×10-3c0s(400t-20mx) m 求：A、人九u。 解：由 y=Ac0s2πyt- x + u y=2x0m4o0-0] m A=2×10-3m

例1：已知波函数 2 10 cos(400 20 ) m 3 y =  t − x − 求：A、、、u。 解：由 2 10 m −3 A =  m 20 2 10 cos 400 3             =  − − x y  t        +      =  −  u x y A cos 2 t

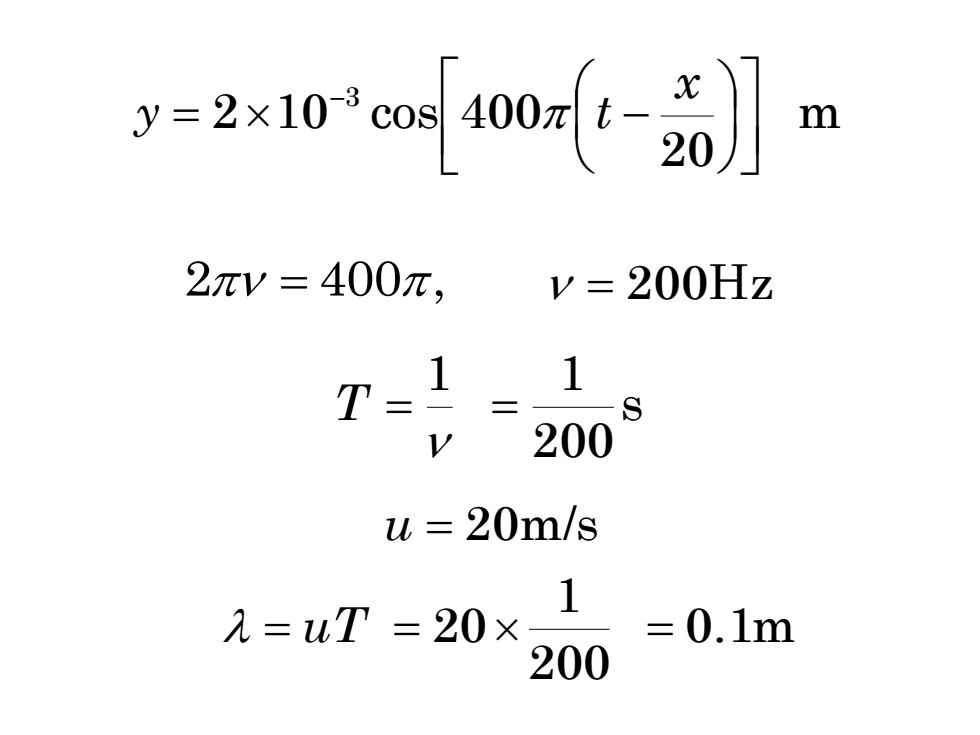
y=2x10oas40s4-20)]m 2πv=400π， 200Hz u 2 m/s 入=uT=20×。 =0.1m 200

2 = 400,  = 200Hz  1 T = s 200 1 = m 20 2 10 cos 400 3             =  − − x y  t 200 1 = 20 u = 20m/s  = uT = 0.1m

例2：振源振动方程为y=6×10-2sin800t 波速u=200m/s,求：①波函数； ②波长、频率；③ x=5m处质点振动与 波源的相位差。 解： ①波源 y=6×10-2c0s(800t-π/2) 波函数 x +0 y=6×10os80-260x12

例2：振源振动方程为 y 6 10 sin800t −2 =  波速 ，求：①波函数； ②波长、频率；③ x = 5m 处质点振动与 波源的相位差。 解： ①波源 波函数        +      =  −  u x y A cos t u = 200m/s 6 10 cos(800 / 2) 2 =   − − y t        −      =  − − /2 200 6 10 cos 800 2   x y t

②.波长、频率 y=Acoi-x +O y=6x10aa800ft-20a2 0=800元 T= 2π 2元 800元 400 v=1/T=400Hz λ=uT=200/400=0.5m

 = 800  2 T =   800 2 = s 400 1 =  = 1/T= 400Hz = 200/ 400 = 0.5m ②.波长、频率        +      =  −  u x y A cos t  = uT        −      =  − − /2 200 6 10 cos 800 2   x y t

③ x=5m质点振动与波源的相位差。 波源 y=6×10-2c0s(800t-π/2) 5m处 y-6x10eas680m?20)a2 波源的相位 01=800t-π/2 x=5m处相位 p2=800π(t-5/200)-π/2 5 相位差 02-91=800π× =20元 200 P点落后反映在相位上为20π，即振源完成10个 全振动后，P点开始振动

③. x = 5m 处相位 相位差 200 5 2 −1 = 800  P 点落后反映在相位上为 20 ， 即振源完成 10 个 全振动后，P 点开始振动。 x = 5m 质点振动与波源的相位差。 波源的相位 1 = 800t − /2 2 = 800 (t − 5/200) − /2 = 20 6 10 cos(800 / 2) 2 =   − − y t        −      =  − − /2 200 6 10 cos 800 2   x y t 波源 5m处