
It is often convenient to change the variable of integration to the collision energy ET=uv2/2.Then k(T)=(8kBT/zp)2[(ET/kBT)oRexp(-ET/kgT)d(ET/kpT) (3.8) where the factor in front of the integral is the thermal(relative)velocity and the integral itself has the dimension of a cross section'. 3.1.2.4 The Tolman interpretation of the activation energy:the reactive reactants The temperature dependence of the reaction rate is determined by the integrals(3.7)or(3.8). The integrand is a product of a rapidly decreasing function,the Boltzmann factor, exp(-ET/kBT),and the energy dependent cross section.For reactions with an energy threshold,in the post threshold regime the cross section will be a rapidly increasing function of the energy,figure 3.3. Note however that the integral is not a thermally averaged cross section.In problem C you show that the integral in(3.8)is an average of the cross section over the thermal flux density of molecules. MRD Chapter 3 page 11 ©R D Levine(2003)
It is often convenient to change the variable of integration to the collision energy ET = µv 2 / 2 . Then k(T) = (8kBT / π µ) (3.8) 1/2 (ET ∫ / kBT)σ R exp(−ET / kBT)d(ET / kBT) where the factor in front of the integral is the thermal (relative) velocity and the integral itself has the dimension of a cross section* . 3.1.2.4 The Tolman interpretation of the activation energy: the reactive reactants The temperature dependence of the reaction rate is determined by the integrals (3.7) or (3.8). The integrand is a product of a rapidly decreasing function, the Boltzmann factor, exp(−ET / kBT), and the energy dependent cross section. For reactions with an energy threshold, in the post threshold regime the cross section will be a rapidly increasing function of the energy, figure 3.3. * Note however that the integral is not a thermally averaged cross section. In problem C you show that the integral in (3.8) is an average of the cross section over the thermal flux density of molecules. MRD Chapter 3 page 11 © R D Levine (2003)
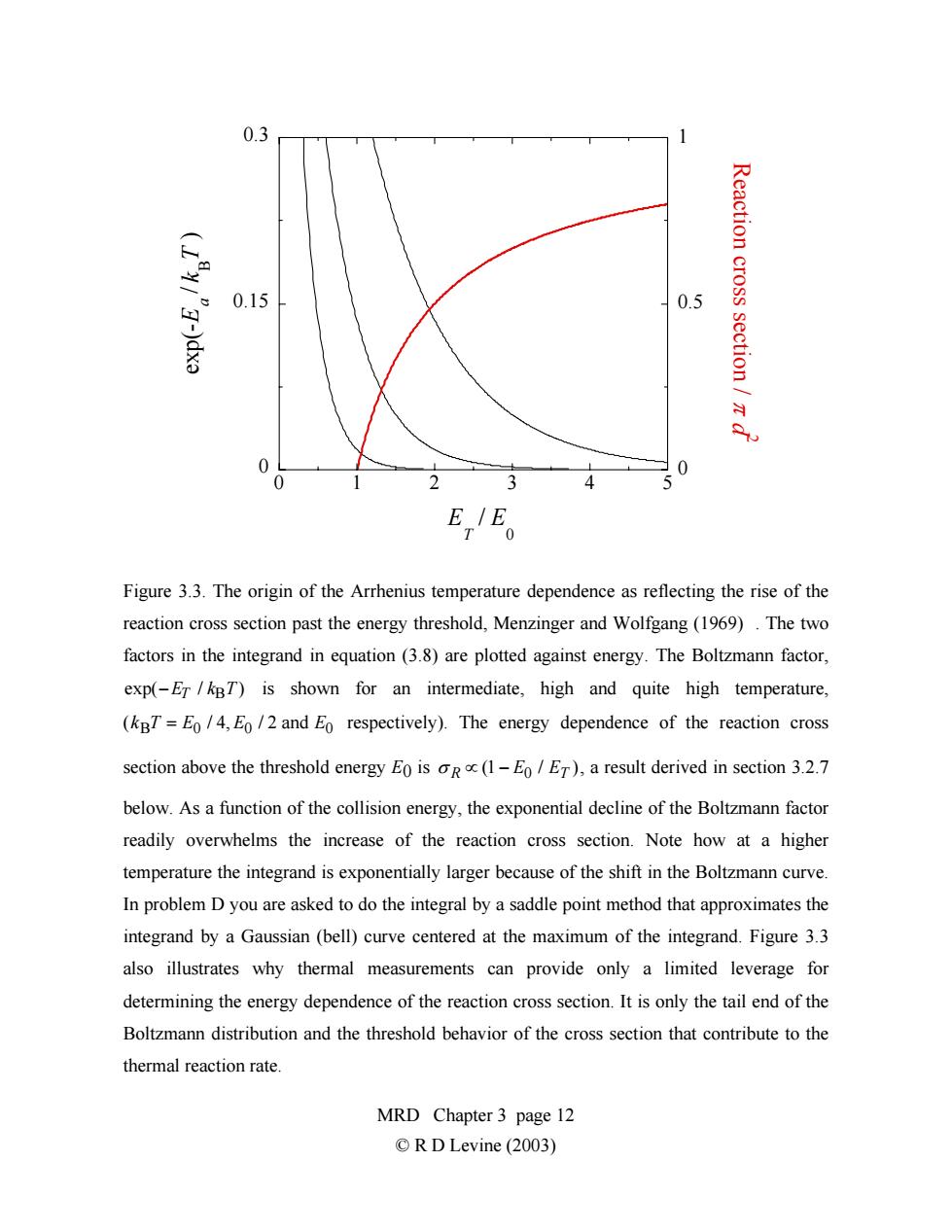
0.3 Reaction cross 0.15 0.5 section /z x 0 0 0 33 4 5 E,E。 Figure 3.3.The origin of the Arrhenius temperature dependence as reflecting the rise of the reaction cross section past the energy threshold,Menzinger and Wolfgang(1969).The two factors in the integrand in equation (3.8)are plotted against energy.The Boltzmann factor, exp(-Er/kBT)is shown for an intermediate,high and quite high temperature, (kBT=Eo/4,Eo/2 and Eo respectively).The energy dependence of the reaction cross section above the threshold energy Eo is oR(1-E/ET),a result derived in section 3.2.7 below.As a function of the collision energy,the exponential decline of the Boltzmann factor readily overwhelms the increase of the reaction cross section.Note how at a higher temperature the integrand is exponentially larger because of the shift in the Boltzmann curve. In problem D you are asked to do the integral by a saddle point method that approximates the integrand by a Gaussian(bell)curve centered at the maximum of the integrand.Figure 3.3 also illustrates why thermal measurements can provide only a limited leverage for determining the energy dependence of the reaction cross section.It is only the tail end of the Boltzmann distribution and the threshold behavior of the cross section that contribute to the thermal reaction rate. MRD Chapter 3 page 12 ©R D Levine(2003)
0 0.15 0.3 0 0.5 1 012345 exp(- E a / kB T ) R e a ctio n c r o s s s e ctio n / π d 2 E T / E 0 Figure 3.3. The origin of the Arrhenius temperature dependence as reflecting the rise of the reaction cross section past the energy threshold, Menzinger and Wolfgang (1969) . The two factors in the integrand in equation (3.8) are plotted against energy. The Boltzmann factor, exp(−ET / kBT) is shown for an intermediate, high and quite high temperature, (kBT = E0 / 4, E0 / 2 and E0 respectively). The energy dependence of the reaction cross section above the threshold energy E0 is σ R ∝ (1 − E0 / ET ), a result derived in section 3.2.7 below. As a function of the collision energy, the exponential decline of the Boltzmann factor readily overwhelms the increase of the reaction cross section. Note how at a higher temperature the integrand is exponentially larger because of the shift in the Boltzmann curve. In problem D you are asked to do the integral by a saddle point method that approximates the integrand by a Gaussian (bell) curve centered at the maximum of the integrand. Figure 3.3 also illustrates why thermal measurements can provide only a limited leverage for determining the energy dependence of the reaction cross section. It is only the tail end of the Boltzmann distribution and the threshold behavior of the cross section that contribute to the thermal reaction rate. MRD Chapter 3 page 12 © R D Levine (2003)

It is then very clear that increasing the temperature will allow the integrand and hence the reaction rate to have a higher value.In problem D you are asked to use a saddle point (approximate)integration to show that an integrand that is a product of an increasing and a decreasing function can be approximated by an Arrhenius form,equation (3.2).Here we proceed to show,following Tolman,that there is always an exact interpretation of the activation energy,equation(3.3),as the excess energy of the collisions that do lead to reaction EaETreactive reactantsETallreactants (3.9) Here reactive reactants means those reactants that do react and the average is over a thermal distribution.The proof is directly from the definition of the activation energy.The proof begins by examining eequation (3.7)and concluding that the entire T dependence of k(T)is due to the Boltzmann factor.We leave it to you to work through the manipulations at the end of which you will conclude that ctive reactantsthe thermal reactat weighe by their raction ae (3.10) (ET aR)exp-ErIkpT)dErET P(ET YET -E红(Er e-er Here P(ET),defined by equation (3.10)is the (normalized)distribution of the reactive reactants.This is the distribution of energy for those pairs of reactants that will react.The average energy of all collisiding pairs is not (3.10)but(3.11) To differentiate k(T)with respect Twhat is needed is to differentiate the thermal Boltzmann factor. Care is needed at one place.The Boltzmann factor carries with it a normalization,(the fore-factor in the last term in(3.7))and this normalization is T-dependent.So it too needs to be differentiated and this is the origin of the second factor in equation(3.9). MRD Chapter 3 page 13 ©R D Levine(2003)
It is then very clear that increasing the temperature will allow the integrand and hence the reaction rate to have a higher value. In problem D you are asked to use a saddle point (approximate) integration to show that an integrand that is a product of an increasing and a decreasing function can be approximated by an Arrhenius form, equation (3.2). Here we proceed to show, following Tolman, that there is always an exact interpretation of the activation energy, equation (3.3), as the excess energy of the collisions that do lead to reaction Ea ≡ ET reactive reactants − ET all reactants (3.9) Here reactive reactants means those reactants that do react and the average is over a thermal distribution. The proof is directly from the definition of the activation energy. The proof begins by examining eequation (3.7) and concluding that the entire T dependence of k(T) is due to the Boltzmann factor. We leave it to you to work through the manipulations* at the end of which you will conclude that ET reactive reactants ≡ ET the thermal reactants weighted by their reaction rate = ET (ET σ R)exp(−ET / kBT)dET ∫ (ET σ R )exp(−ET / kBT) dET ∫ ≡ ET Prr(ET ) ∫ dET (3.10) Here Prr(ET ) , defined by equation (3.10) is the (normalized) distribution of the reactive reactants. This is the distribution of energy for those pairs of reactants that will react. The average energy of all collisiding pairs is not (3.10) but (3.11) * To differentiate k(T) with respect T what is needed is to differentiate the thermal Boltzmann factor. Care is needed at one place. The Boltzmann factor carries with it a normalization, (the fore-factor in the last term in (3.7)) and this normalization is T-dependent. So it too needs to be differentiated and this is the origin of the second factor in equation (3.9). MRD Chapter 3 page 13 © R D Levine (2003)

Eall reactantsEthe thermal reactants (3.11) EY2 exp(-ET /kpT)dET =可B了Eexp-所1keDr When we recognize that,strictly speaking,the activation energy is really a thermal average many puzzles go away.The activation energy is not,for example,the minimal energy for reaction.It is closely related to it because the reactive reactants need to have at least the minimal energy,but they can have more than the minimal amount and indeed the reaction cross section typically rises steeply in the post threshold regime,figure 3.1.Nor does the activation energy have to be independent of temperature.Atypically the activation energy can even be negative if low energy collisions preferentially lead to reaction3. Show,problem E,that this dependence tells us about the entropic requirements of the reaction.We provide a microscopic view of such requirements in chapter 5. MRD Chapter 3 page 14 ©R D Levine(2003)
ET all reactants ≡ ET the thermal reactants = ET ET 1/2 exp(−ET / kBT)dET ET 1/2 ∫ exp(−ET / kBT)dET ∫ (3.11) When we recognize that, strictly speaking, the activation energy is really a thermal average many puzzles go away. The activation energy is not, for example, the minimal energy for reaction. It is closely related to it because the reactive reactants need to have at least the minimal energy, but they can have more than the minimal amount and indeed the reaction cross section typically rises steeply in the post threshold regime, figure 3.1. Nor does the activation energy have to be independent of temperature* . Atypically the activation energy can even be negative if low energy collisions preferentially lead to reaction4 . * Show, problem E, that this dependence tells us about the entropic requirements of the reaction. We provide a microscopic view of such requirements in chapter 5. MRD Chapter 3 page 14 © R D Levine (2003)

Appendix 3.A.Reaction rate under non-equilibrium conditions On a microscopic,molecular level,we can write for a state selected and state resolved reaction F+HCI()→CI+HF() where i and j label the different internal states.We assume here that the kinetic energy has a thermal distribution.The observed bulk reaction rate at complete thermal equilibrium is then a sum over the rates of reaction of the HCI molecules,in all possible states,with F atoms, -∑k(TEHC6] (A.3.1) dt Here k(T)is the reaction rate constant for a selected state of the reactants.Whether the system is in thermal equilibrium over the internal states of HCl or not,we can rewrite(A.3.1) as 四-∑k(D [HCID HCI=K(TXFIHCI] (A.3.2) dt [HCI] where [HCI]is the total concentration of HCl.By comparison to equation(3.1)this defines a reaction rate constant,k(T)as k(T)=∑nHC0=∑P,k(D (A.3.3) [HCI] i Here Pi,as defined by equation(A.3.3),is the relative population (=mol fraction)of HCI molecules in the state i [HCI(O] Pi= (A.3.4) [HCI] In general pi can depend on time and so equation(A.3.3)does not necessarily define a rate constant.If however the system is in thermal equilibrium at the temperature T then pi is the MRD Chapter 3 page 15 ©R D Levine(2003)
Appendix 3.A. Reaction rate under non-equilibrium conditions On a microscopic, molecular level, we can write for a state selected and state resolved reaction F + HCl(i) → Cl + HF( j) where i and j label the different internal states. We assume here that the kinetic energy has a thermal distribution. The observed bulk reaction rate at complete thermal equilibrium is then a sum over the rates of reaction of the HCl molecules, in all possible states, with F atoms, − d[F] dt = ki(T)[F][HCl(i)] i ∑ (A.3.1) Here ki(T) is the reaction rate constant for a selected state of the reactants. Whether the system is in thermal equilibrium over the internal states of HCl or not, we can rewrite (A.3.1) as − d[F] dt = ki(T)[F][HCl(i)] [HCl] [HCl] i ∑ = k(T)[F][HCl] (A.3.2) where [HCl] is the total concentration of HCl. By comparison to equation (3.1) this defines a reaction rate constant, k(T) as k(T) = ki(T) [HCl(i)] [HCl] i ∑ ≡ pi i ∑ ki(T) (A.3.3) Here pi , as defined by equation (A.3.3), is the relative population (=mol fraction) of HCl molecules in the state i pi = [HCl(i)] [HCl] (A.3.4) In general pi can depend on time and so equation (A.3.3) does not necessarily define a rate constant. If however the system is in thermal equilibrium at the temperature T then pi is the MRD Chapter 3 page 15 © R D Levine (2003)