
电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC A Brief History Stephane Mallat ■l988:Mallat算法 法国科学家Stephane Mallat提出多分辨率概念,从空间上形 象说明小波的多分辨率特性,随着尺度由大到小变化,在各尺 度上可以由粗到细的观察图像的不同特征的一种算法。并提出 了正交小波的构造方法和快速算法,称为Mallat:算法。 该算法统一了在此之前构造正交小波基的所有方法,其地位相 当于FFT在经典傅立叶分析中的地位
◼ 1988:Mallat算法 ◼法国科学家Stephane Mallat提出多分辨率概念,从空间上形 象说明小波的多分辨率特性,随着尺度由大到小变化,在各尺 度上可以由粗到细的观察图像的不同特征的一种算法。并提出 了正交小波的构造方法和快速算法,称为Mallat算法。 ◼该算法统一了在此之前构造正交小波基的所有方法,其地位相 当于FFT在经典傅立叶分析中的地位。 Stephane Mallat A Brief History

电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC A Brief History ■1988:Mallat算法 Stephane Mallat Mallat算法:小波分解与重构 y,='-®W- ='-2⊕W-2®W-
◼ 1988:Mallat算法 ◼Mallat算法:小波分解与重构 Stephane Mallat A Brief History 1 1 2 2 1 ... j j j jjj V V W V W W − − −−− = = =
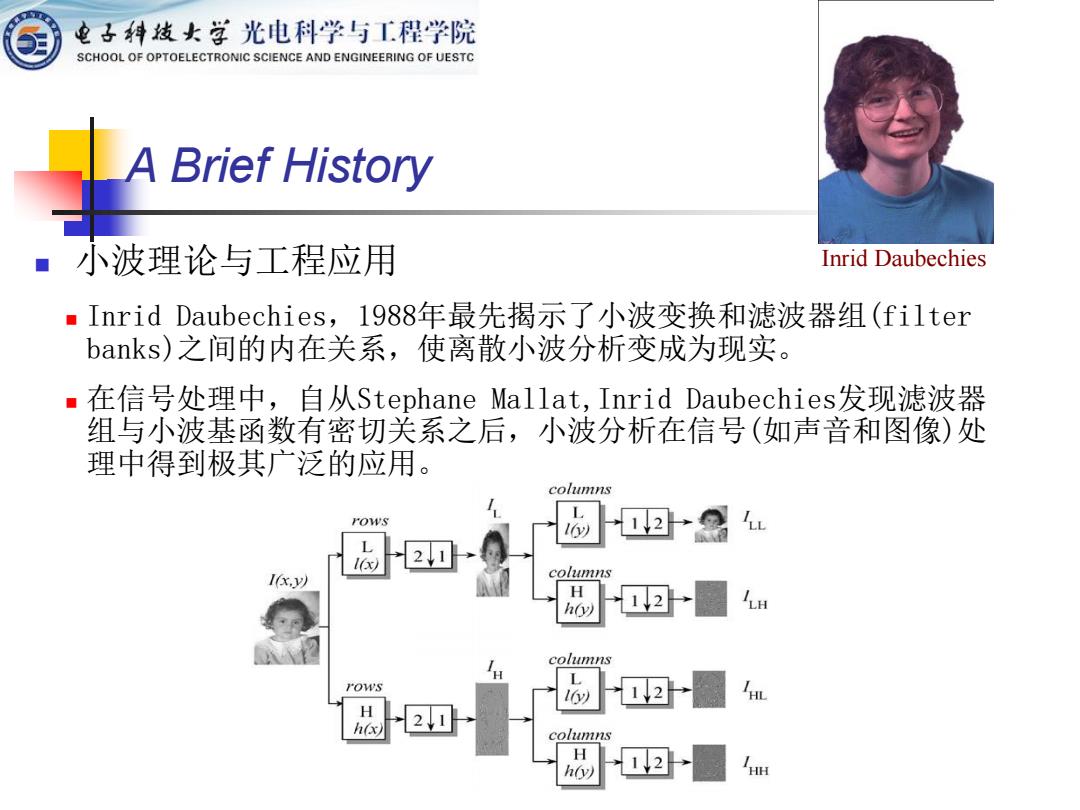
电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC A Brief History 小波理论与工程应用 Inrid Daubechies ■Inrid Daubechies,1988年最先揭示了小波变换和滤波器组(filter banks)之间的内在关系,使离散小波分析变成为现实。 ■在信号处理中,自从Stephane Mallat,Inrid Daubechies发现滤波器 组与小波基函数有密切关系之后,小波分析在信号(如声音和图像)处 理中得到极其广泛的应用。 columns L FOWS l) L Ix) 210 1x,以 columns H h0) columns L rOWS 16 12 H h(x) 21 columns H hy) 2 /:t
◼ 小波理论与工程应用 ◼ Inrid Daubechies,1988年最先揭示了小波变换和滤波器组(filter banks)之间的内在关系,使离散小波分析变成为现实。 ◼ 在信号处理中,自从Stephane Mallat,Inrid Daubechies发现滤波器 组与小波基函数有密切关系之后,小波分析在信号(如声音和图像)处 理中得到极其广泛的应用。 Inrid Daubechies A Brief History

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC A Brief History(Summary) 时间 标志性事件 人物 1822 Fourier变换,在频域的定位最准确,无任何时域 Fourier 定位能力。如:δ函数,时域定位完全准确,频域 无任何定位能力。 1910 提出规范正交基。 Harr 1946 Gabor?变换(STFT),窗函数的大小和形状与时间和 Gabor 频率无关而保持固定不变。不构成正交基。 1984 提出连续小波变换。 Morlet 1985 提出离散小波变换。 Meyer,Daubecies 1986 Meyeri证明了不可能存在时域频域同时具有正则性 Meyer 的正交小波基,证明了小波的自正交性。 1987 统一了多分辨率分析和小波变换,给出了快速算 Mallat 法。 1988 Daubecies在NSF的小波专题研讨会进行了讲座。 Daubecies
时 间 标志性事件 人物 1822 Fourier变换,在频域的定位最准确,无任何时域 定位能力。如:δ函数,时域定位完全准确,频域 无任何定位能力。 Fourier 1910 提出规范正交基。 Harr 1946 Gabor变换(STFT),窗函数的大小和形状与时间和 频率无关而保持固定不变。不构成正交基。 Gabor 1984 提出连续小波变换。 Morlet 1985 提出离散小波变换。 Meyer,Daubecies 1986 Meyer证明了不可能存在时域频域同时具有正则性 的正交小波基,证明了小波的自正交性。 Meyer 1987 统一了多分辨率分析和小波变换,给出了快速算 法。 Mallat 1988 Daubecies在NSF的小波专题研讨会进行了讲座。 Daubecies A Brief History (Summary)

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Outline Background Multiresolution Expansions Wavelet Transforms in One Dimension The Fast Wavelet Transform Wavelet Transforms in Two Dimensions ◆Vavelet Packets
Outline ◆ Background ◆ Multiresolution Expansions ◆ Wavelet Transforms in One Dimension ◆ The Fast Wavelet Transform ◆ Wavelet Transforms in Two Dimensions ◆ Wavelet Packets