
电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC chapterd4fiteingintheFftegμegylonatin

电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC Outline Background Preliminary Concepts Sampling and the Fourier Transform of Sampled Functions The Discrete Fourier Transform of One Variable Extension to Functions of Two Variables Some Properties of the 2-D Discrete Fourier Transform The Basics of Filtering in the Frequency Domain Image Smoothing Using Frequency Domain Filters Image Sharpening Using Frequency Domain Filters Selective Filtering
Outline ◆ Background ◆ Preliminary Concepts ◆ Sampling and the Fourier Transform of Sampled Functions ◆ The Discrete Fourier Transform of One Variable ◆ Extension to Functions of Two Variables ◆ Some Properties of the 2-D Discrete Fourier Transform ◆ The Basics of Filtering in the Frequency Domain ◆ Image Smoothing Using Frequency Domain Filters ◆ Image Sharpening Using Frequency Domain Filters ◆ Selective Filtering

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC 4.1 Background Agenda A Brief History of the Fourier Series and Transform
A Brief History of the Fourier Series and Transform 4.1 Background Agenda

电子科发女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC A Brief History Jean Baptiste Joseph Fourier: French mathematician,born in 1768 in the town of Auxerre. ■ Fourier's contribution states that any periodic function can be expressed as the sum of sines and/or cosines of different frequencies,each multiplied by a different coefficient (we now Fourier(1768-1830) call this sum a Fourier series)
A Brief History ◼ Jean Baptiste Joseph Fourier: French mathematician, born in 1768 in the town of Auxerre. ◼ Fourier’s contribution states that any periodic function can be expressed as the sum of sines and/or cosines of different frequencies, each multiplied by a different coefficient (we now call this sum a Fourier series). Fourier(1768 –1830)
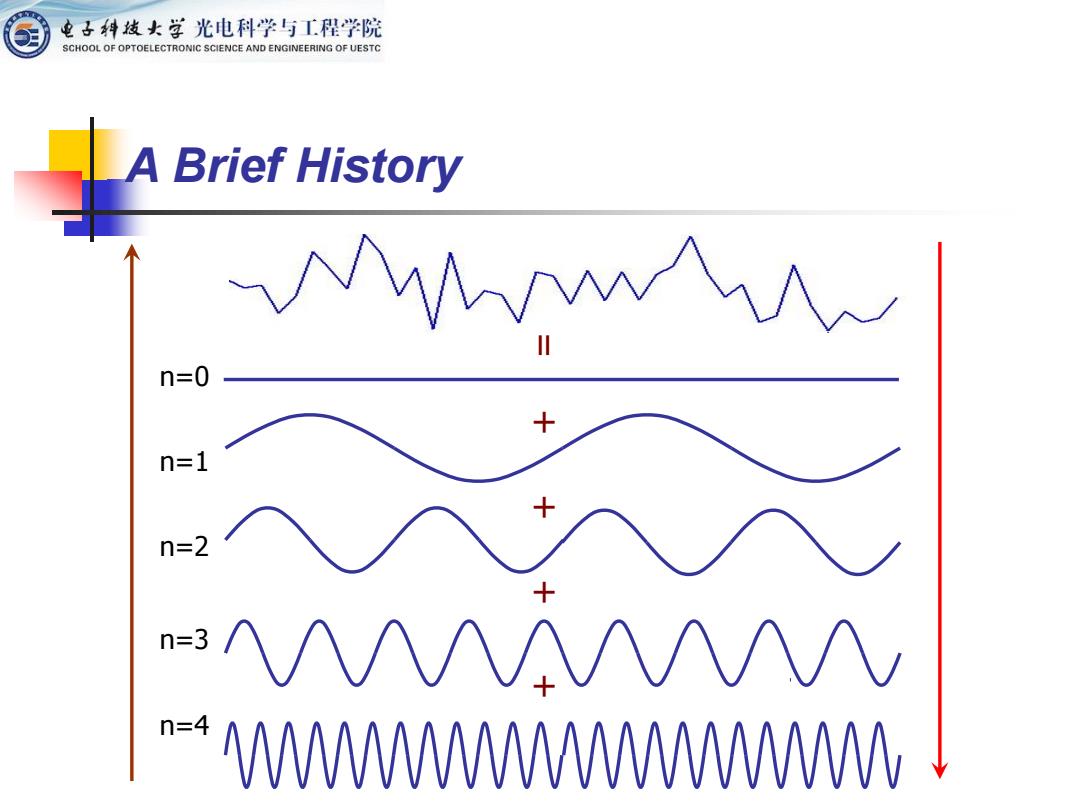
电子科线女学光电科学与工程学院 SCHOOL OF OPTOELECTRONIC SCIENCE AND ENGINEERING OF UESTC A Brief History w n=0 × n=1 n=2 n=3 n=4 WWWM
= + + + + n=0 n=1 n=2 n=3 n=4 A Brief History