
信号处理理论与算法 短时傅里叶变换与Gabor3变换 张朋 自动化工程学院
信号处理理论与算法 短时傅里叶变换与Gabor变换 张 朋 自动化工程学院
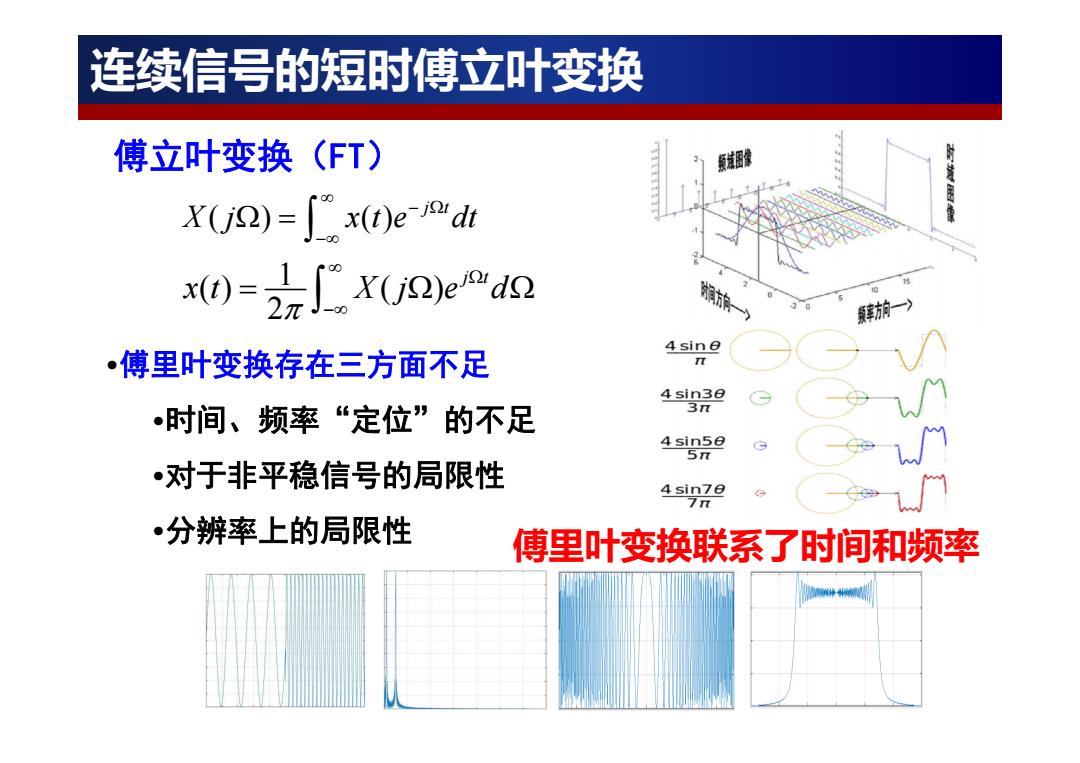
连续信号的短时傅立叶变换 傅立叶变换(FT) 原超拿 X(j)=["x(t)e-dr x)=2元JX(U2e0 4sine ●傅里叶变换存在三方面不足 4sin30 时间、频率“定位”的不足 3π 4sin5e 5π •对于非平稳信号的局限性 4sin7e 7π •分辨率上的局限性 傅里叶变换联系了时间和频率
傅立叶变换(FT) ( ) () j t X j x t e dt 1 () ( ) 2 j t xt X j e d 傅里叶变换联系了时间和频率 连续信号的短时傅立叶变换 •傅里叶变换存在三方面不足 •时间、频率“定位”的不足 •对于非平稳信号的局限性 •分辨率上的局限性

连续信号的短时傅立叶变换 短时傅立叶变换(STFT) 用基函数8,n(t)=g(t-t)eR来代替傅立叶变换中的基函数e2r STFT定义: 给定信号x(t)∈L(R)其STFT定义为: STFT,(t,)=x()gia()dt =[x(t)g'(r-t)e-dr =<x(r),g(r-t)e> 式中8.(t)=g(t-t)e2i Ig()1 8.(t)l=1 窗函数8(T)取对称函数
用基函数 j t g ( ) g(t )e , 来代替傅立叶变换中的基函数 j t e 短时傅立叶变换(STFT) 连续信号的短时傅立叶变换 给定信号 其STFT定义为 : 式中 窗函数 取对称函数。 ( ) ( ) 2 x t L R j j x t x g t e d x g t e STFT t x g d ( ) ( ) ( ), ( ) ( , ) ( ) ( ) * * , j t g ( ) g( t)e , || g( ) || 1 || ( ) || 1 gt, g( ) STFT定义:
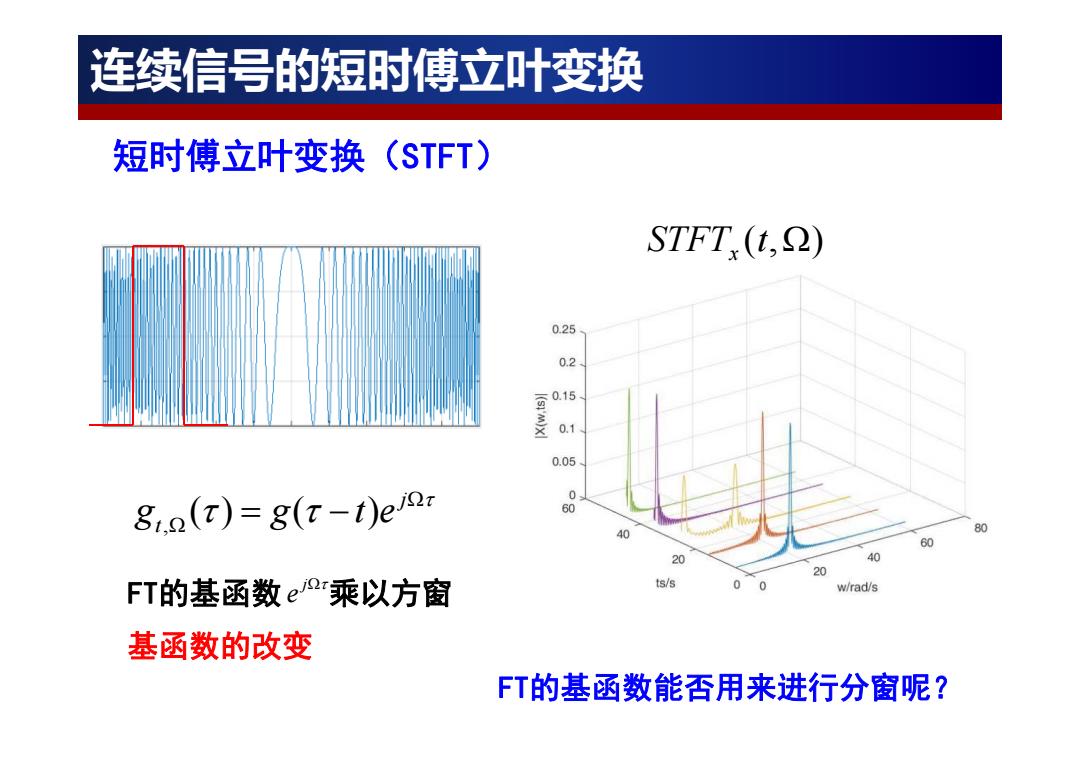
连续信号的短时傅立叶变换 短时傅立叶变换(STFT) STFT.(t,) 0.25 0.2 0.15 (sM)x 0.1 0.05 0 8.(t)=8(x-t)e2i 60 90 80 20 40 20 FT的基函数eP乘以方窗 ts/s 0 w/rad/s 基函数的改变 FT的基函数能否用来进行分窗呢?
FT的基函数 乘以方窗 , () ( ) j t g g te j e 基函数的改变 STFT (t,) x FT的基函数能否用来进行分窗呢? 连续信号的短时傅立叶变换 短时傅立叶变换(STFT)
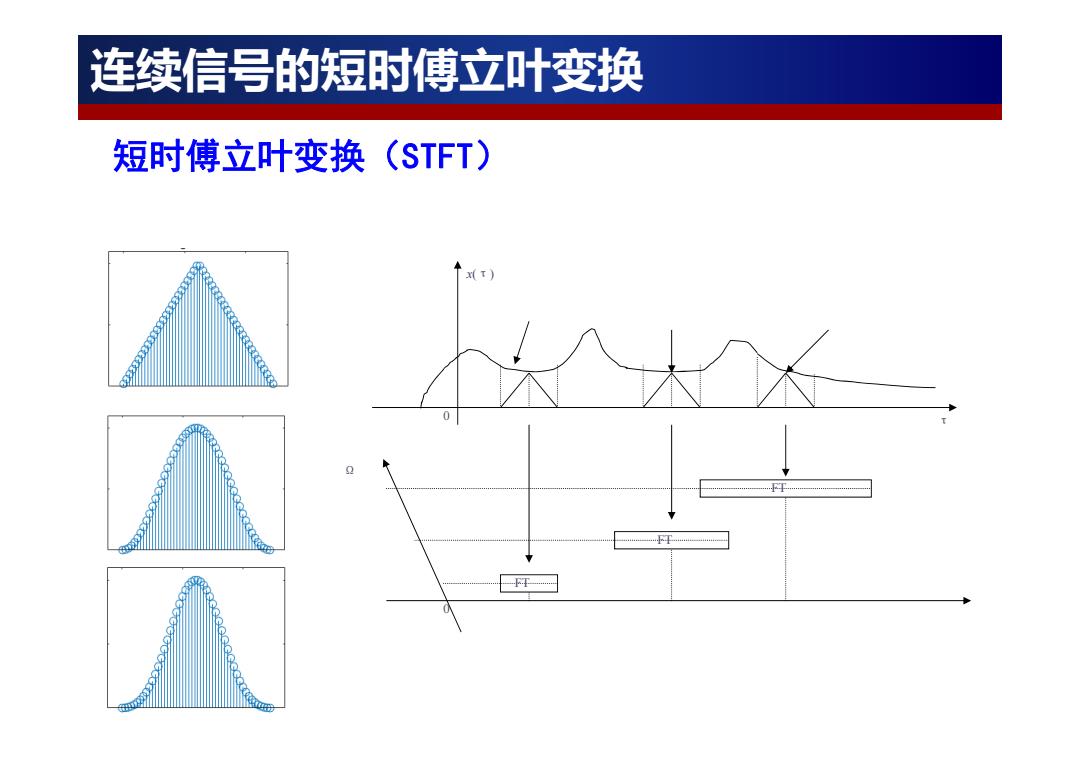
连续信号的短时傅立叶变换 短时傅立叶变换(STFT) X(T
τ x(τ) 0 FT FT FT Ω 0 连续信号的短时傅立叶变换 短时傅立叶变换(STFT)