
核心重难探究 第三步:通过取0和1的平均数缩小x所在的范围; 取=当号时 当x=1时>0,1<1. 2 (1)请仿照第二步,通过运算,验证2x2+x-2=0的另一个根x2所 在范围是-2<x2<-1; (2)在-2<x2<-1的基础上,重复应用第三步中取平均数的方法, 将x,所在范围缩小至<x,<n,使得n-m≤. 导航页
导航页 核心重难探究 第三步:通过取0和1的平均数缩小x1所在的范围; 取 x= 𝟎+𝟏 𝟐 = 𝟏 𝟐 ,∵当 x= 𝟏 𝟐 时,y<0; 当 x=1 时,y>0,∴ 𝟏 𝟐 <x1<1. (1)请仿照第二步,通过运算,验证2x 2+x-2=0的另一个根x2所 在范围是-2<x2<-1; (2)在-2<x2<-1的基础上,重复应用第三步中取平均数的方法, 将x2所在范围缩小至m<x2<n,使得n-m≤ . 𝟏 𝟒
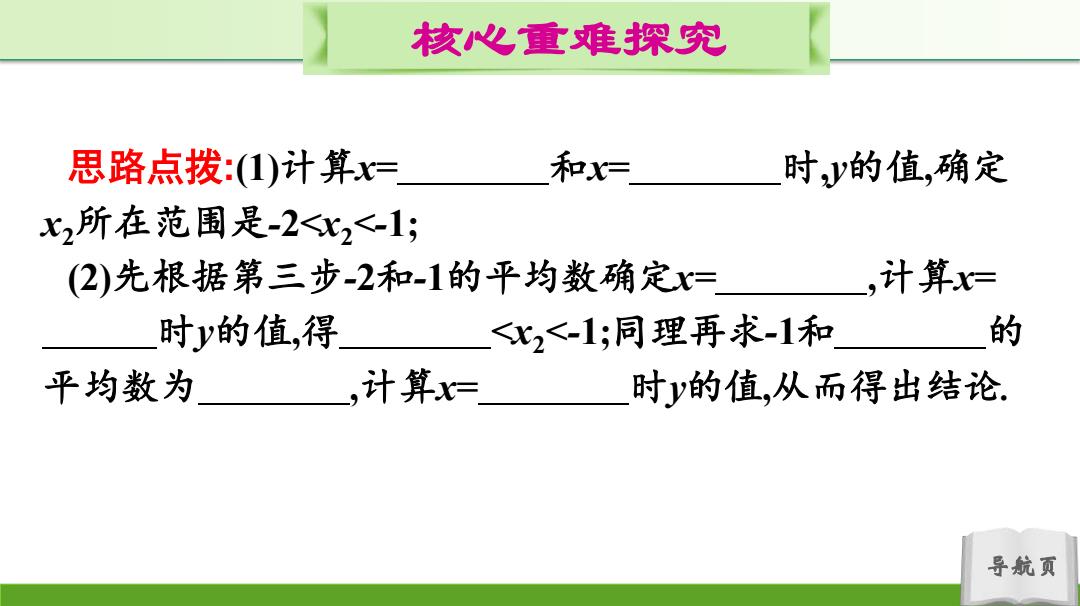
核心重难探究 思路点拨:1)计算x= 和x= 时y的值,确定 x2所在范围是-2<x2<-1; (2)先根据第三步-2和-1的平均数确定x= ,计算= 时y的值,得 <x2<-1;同理再求-1和 的 平均数为■ ,计算= 时y的值,从而得出结论. 导航页
导航页 核心重难探究 思路点拨:(1)计算x= 和x= 时,y的值,确定 x2所在范围是-2<x2<-1; (2)先根据第三步-2和-1的平均数确定x= ,计算x= 时y的值,得 <x2<-1;同理再求-1和 的 平均数为 ,计算x= 时y的值,从而得出结论

核心重难探究 解:(1).当=2时y>0; 当x=1时y<0; ∴.方程2x2+x-2=0的另一个根x2所在的范围是-2<x2<-1. 2取20-2 22 :当x时-2x足-22=10: 当x=-1时y=1<0; 导航页
导航页 核心重难探究 解:(1)∵当x=-2时,y>0; 当x=-1时,y<0; ∴方程2x 2+x-2=0的另一个根x2所在的范围是-2<x2<-1. (2)取 x= (-𝟐)+(-𝟏) 𝟐 =- 𝟑 𝟐 , ∵当 x=- 𝟑 𝟐 时,y=2× 𝟗 𝟒 − 𝟑 𝟐 -2=1>0; 当 x=-1 时,y=-1<0; ∴- 𝟑 𝟐 <x2<-1