
当入2=入3=1时,解方程(A一E)x=0由 7-2 A-E= 得基础解系P2= -2 所以k2,(k≠0)是对应于入2=)3=的全部特征向量 -211 例3求矩阵A= 0 2 0 的特征值和特征向量 -41
当2 = 3 =1时 ,解方程(A-E)x = 0由 − − − = 1 0 1 4 2 0 2 1 0 A E ~ 0 0 0 0 1 2 1 0 1 得基础解系 − − = 1 2 1 2 p 例3 求矩阵 − − = 4 1 3 0 2 0 2 1 1 A 的特征值和特征向量 所以k p2 (k 0)是对应于2 = 3 =1的全部特征向量

解(1)由A一入E=0,求A的全部特征值。 -2-λ 2-入 3-入 -e-2g =(2-入22-入-2) =-(入+1入-2}=0 得A的特征值为入,=一1入2=入3=2
解 (1)由︱A-λE︱=0,求A的全部特征值。 − − − − − − = 4 1 3 0 2 0 2 1 1 A E ( ) − − − − = − 4 3 2 1 2 (2 )( 2) 2 = − − − ( 1)( 2) 0 2 = − + − = 得A的特征值为 1 = −1 2 = 3 = 2
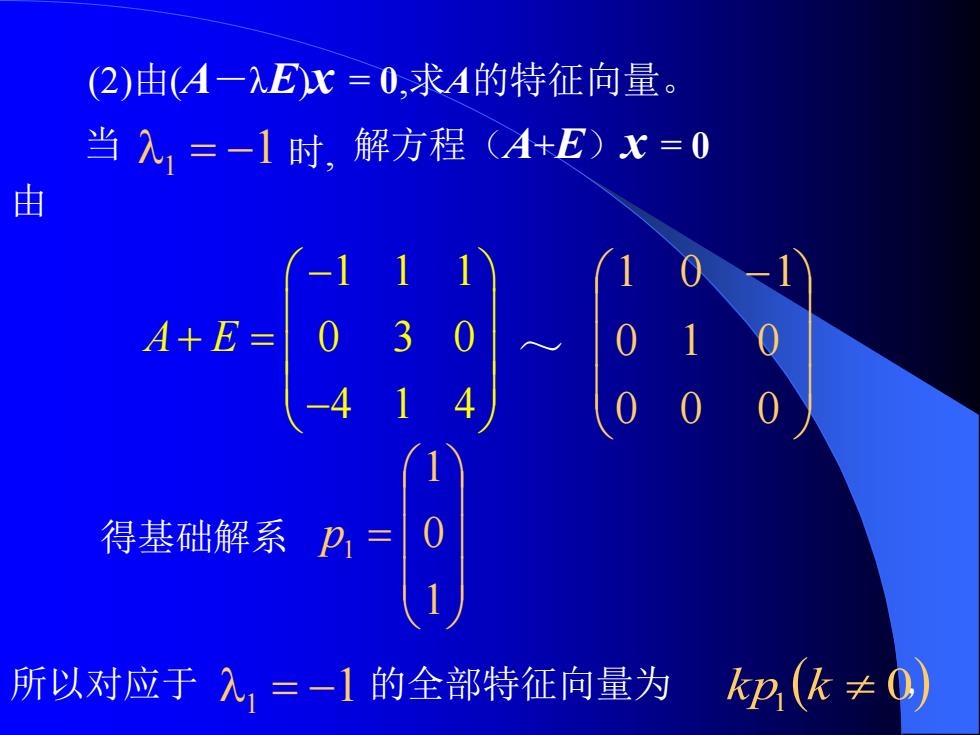
(2)由(A一入E)X=0,求A的特征向量。 当入,=一1时,解方程(A+E)x=0 由 得基础解系P,= 所以对应于入,=-1的全部特征向量为k2(飞≠0)
(2)由(A-λE)x = 0,求A的特征向量。 当 1 = −1 时, 解方程(A+E)x = 0 由 1 1 1 0 3 0 4 1 4 A E − + = − ~ − 0 0 0 0 1 0 1 0 1 得基础解系 = 1 0 1 1 p 所以对应于 1 = −1 的全部特征向量为 ( 0,) kp1 k

当入2=入3=2时 解方程(A一2E)x=0,由 2可0 得基础解系 所以对应于入2=入3=2的全部特征向量 飞2P2+k3P3(亿2,k不同时为零
当2 = 3 = 2时 解方程(A-2E)x = 0 ,由 − − − = 4 1 1 0 0 0 4 1 1 A 2E ~ − 0 0 0 0 0 0 4 1 1 得基础解系 = − = 4 0 1 1 1 0 2 3 p , p 所以对应于2 = 3 = 2的全部特征向量 2 2 3 p3 k p + k ( 不同时为零) 2 3 k ,k

例4设)是方阵A的特征值,则22是A的特征值: 证因为入是方阵A的特征值,设为P0,使 AP=λP 于是 APP=A(4P)=A0P)=(4P)=(0P)=入2P 所以,2是4的特征值 例5设3阶方阵A满足A3-3A2+2A=0,求A的特征值 解设入是A的特征值,x是A的关于)所对应的特征向量 则AX=)X,从而4一32x+2Ax=0 (23-322+2见)x=0又x0 所以 入3-3元2+2入=0,从而(22-3%+2)=0
例4 设λ是方阵A的特征值, 证 因为λ是方阵A的特征值,设为P ≠0,使 AP = λP, 于是 A P = A(AP) 2 = A(P) = (AP) ( P) P 2 = = 所以 2 是A 2 的特征值 例5 设3阶方阵A满足 求A的特征值 解 设λ是A的特征值, x是 A 的关于 λ 所对应的特征向量 则Ax = λx,从而 3 2 0 3 2 A x − A x + Ax = 3 2 0, 3 2 A − A + A= 又 x≠0, 3 2 0, 3 2 所以 − + = 3 2 0 2 从而 ( − + ) = 3 2 ( 3 2 ) 0 − + = x 2 2 则 是 的特征值. A