《概率论与数理统计》课程教学资源（PPT课件）第三章 多维随机变量及其分布 第五节 两个随机变量的函数的分布

概率伦与数程统外 P(max(X,Y)=i) 0 1 =PX=i,Y<i 0 1/22 1/22 +P{X≤i,Y=i} 1 1/22 1/22 →P{max(X,Y)=0=P{0,0} 1 22 P{max(X,Y)=1FP{1,0}+P{0,1}+P{1,1} 1,113 22 23+ 2222 故Z=max(X,Y)Z 0 的分布律为 4

P{max(X,Y ) = i} = P{X = i,Y  i} + P{X  i,Y = i}  P{max(X,Y ) = 0}= P{0,0} , 2 1 2 = P{max(X,Y ) = 1}= P{1,0}+ P{0,1}+ P{1,1} 2 2 2 2 1 2 1 2 1 = + + . 2 3 2 = 的分布律为 故Z = max( X,Y ) Z P 0 1 4 3 4 1 X Y 0 1 1 0 2 1 2 2 1 2 2 1 2 2 1 2

概车纶与散理统外「 三、连续型随机变量函数的分布 1.Z=X+Y的分布 设(X,Y)的概率密度为f(x,y),则Z=X+Y 的分布函数为 Fz(a)=PZ≤z=∬fx,)dxdy◆X x+y≤ x+y=7 fdxdy x-u-yf fu-x.ydudy =∫[afu-y)dy]aa

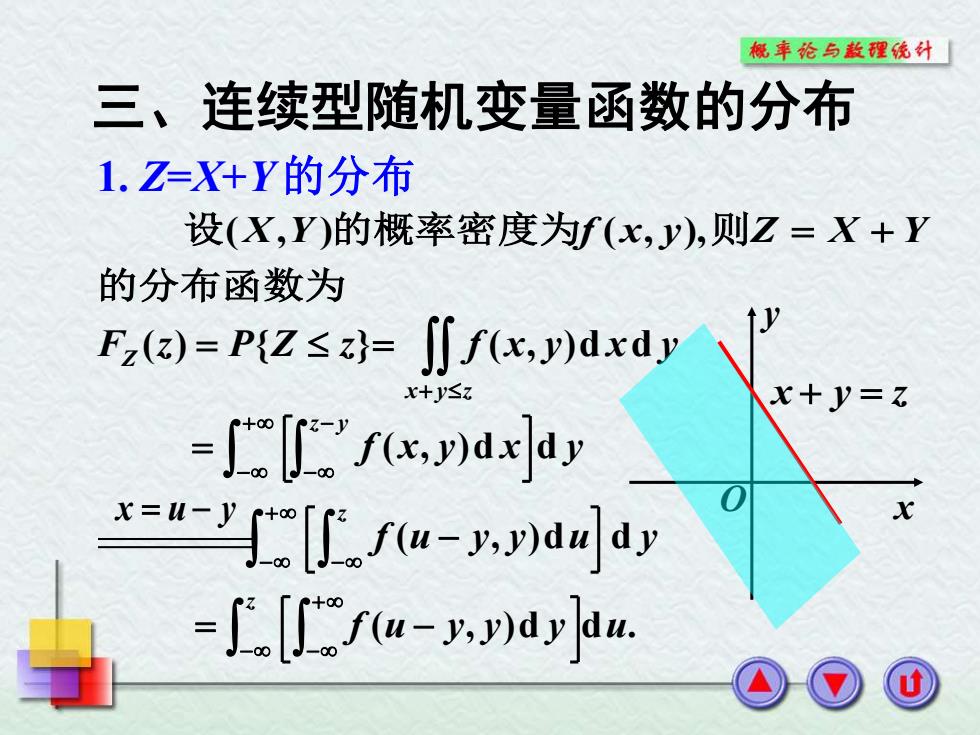
的分布函数为 设(X,Y )的概率密度为f (x, y),则Z = X + Y F (z) P{Z z} Z =  f x y x y x y z ( , )d d  +  = x y O x + y = z x = u − y 三、连续型随机变量函数的分布 1. Z=X+Y 的分布 f x y x y z y ( , )d d   + − − − = f u y y u y z ( , )d d   + − − − f (u y, y)d y du. z −  + − = −

概率伦与款理统外 由此可得概率密度函数为 f&)=fa-,)d. 由于X与y对称，fz(z)=」f(x,z-)dx. 当X,Y独立时，fz(z)也可表示为 f()=[fx(z-y)f(y)dy, fz(z)=[fx(x)f(z-x)dx

由此可得概率密度函数为 ( ) ( , )d .  + − f z = f z − y y y Z f (z) f (x,z x)d x. Z  + − 由于 X 与 Y 对称, = − 当 X, Y 独立时, fZ (z)也可表示为 ( ) ( ) ( )d ,  + − f z = f z − y f y y Z X Y f (z) f (x) f (z x)d x . Z  X Y + − 或 = −

概率伦与散理统针」 例4设两个独立的随机变量X与Y都服从标准正 态分布，求Z=X+Y的概率密度. 解由于f=↓ =e2,-0<x<+o0, √2 0四三云 =e2,-o<y<+oo, 由公式fz(z)=fx(x)fr(z-x)dx

由公式 f (z) f (x) f (z x)d x, Z  X Y + − = − 解 e , , 2π 1 ( ) 2 2 = −    + − f x x x 由于 X e , , 2π 1 ( ) 2 2 = −    + − f y y y Y 例4 设两个独立的随机变量 X 与Y 都服从标准正 态分布,求 Z=X+Y 的概率密度