复旦大学：《集成电路工程》教学资源（学士士学位论文）单管和双管放大器的频响分析

第三章单管放大器的频率响应特性 第三章单管放大器的频率响应特性 本章中，我们由简单的单管放大器一共源放大器开始。虽然看起来过于简单，但是 它已经包含两个节点，即输入节点和输出节点。因此共源放大器是所有两阶放大器的代 表，将会被详细研究。重要的传输特性，比如增益、输入和输出阻抗将被讨论。其他重 要的现象比如极点分离、正负零点、密勒效应也将会涉及。其次是阻抗转换电路一源极 跟随器，它的从高阻抗到低阻抗转换的缓冲能力随频率的变化将会被仔细讨论。然后， 讨论用于从低阻抗到高阻抗转换的共栅放大器。 3.1共源放大器 如图3-1所示，给出了带电阻负载及电阻偏置的单管共源放大器。Rs是信号源电压 源内阻，Cc是信号通路上的耦合电容，R1和R2是设置静态工作点的偏置电阻，R是 负载（这里假设电阻负载）。电容C℃一般比较大，将其视为高频交流短路，画出小信号 等效电路图如图3-1。R12是电阻R1和R2的并联电阻，考虑一般性，假设R12>>Rs, 忽略R12。 因为这个电路包含两个节点，所有的器件电容和寄生电容都可以归为以下三类： ①输入节点到地之间的电容，称为Cgs: ②输出节点到地之间的电容，称为Cds: ③输出节点到输入节点之间的电容，称为Cgd。 通过Laplace变换，可以将增益传输函数计算为复数频率的函数；每个电容被表示为阻 抗1/sC,其中S=jw. Voo R Rs VIN (a） (b) 图3-1共源放大器及其小信号等效电路图 根据小信号等效电路，利用节点电压法可以得到增益Av和输入阻抗Zn、输出阻抗 Zut的完整表达式。接下来将会看到，尽管电路中有3个节点电容，但是传输函数的分 母仅仅是二阶的，这是因为3个节点电容组成了一个环路，在电路中只允许存在两个独 立的初始条件，所以产生的是对时间的二阶微分方程

第三章 单管放大器的频率响应特性 11 第三章 单管放大器的频率响应特性 本章中，我们由简单的单管放大器—共源放大器开始。虽然看起来过于简单，但是 它已经包含两个节点，即输入节点和输出节点。因此共源放大器是所有两阶放大器的代 表，将会被详细研究。重要的传输特性，比如增益、输入和输出阻抗将被讨论。其他重 要的现象比如极点分离、正负零点、密勒效应也将会涉及。其次是阻抗转换电路--源极 跟随器，它的从高阻抗到低阻抗转换的缓冲能力随频率的变化将会被仔细讨论。然后， 讨论用于从低阻抗到高阻抗转换的共栅放大器。 3.1 共源放大器 如图 3-1 所示，给出了带电阻负载及电阻偏置的单管共源放大器。RS是信号源电压 源内阻，CC 是信号通路上的耦合电容，R1 和 R2 是设置静态工作点的偏置电阻，RL 是 负载（这里假设电阻负载）。电容 CC一般比较大，将其视为高频交流短路，画出小信号 等效电路图如图 3-1。R12 是电阻 R1 和 R2 的并联电阻，考虑一般性，假设 R12>>RS， 忽略 R12。 因为这个电路包含两个节点，所有的器件电容和寄生电容都可以归为以下三类： ①输入节点到地之间的电容，称为 Cgs； ②输出节点到地之间的电容，称为 Cds； ③输出节点到输入节点之间的电容，称为 Cgd。 通过 Laplace 变换，可以将增益传输函数计算为复数频率的函数；每个电容被表示为阻 抗 1/sC,其中 s=jω。 RS VDD VSS CC Rin R1 RL Rout vOUT vIN R2 gmvgs Cds rds RL vout Cgd R12 Cgs vgs RS vin RS ’ ZL ’ RL Z ’ in Zout (a) (b) 图 3-1 共源放大器及其小信号等效电路图 根据小信号等效电路，利用节点电压法可以得到增益 AV和输入阻抗 Zin、输出阻抗 Zout 的完整表达式。接下来将会看到，尽管电路中有 3 个节点电容，但是传输函数的分 母仅仅是二阶的，这是因为 3 个节点电容组成了一个环路，在电路中只允许存在两个独 立的初始条件，所以产生的是对时间的二阶微分方程

单管和双管放大器的频响分析 3.1.1单独考虑各个电容 我们先单独考虑各个电容对频率响应特性的影响。 (1)只考虑电容Cgs 很容易可以求出增益为 Ao A=1+ (3.1) 其中 Ao=-9mRL (3.2) 表示低频增益： 1 fo=2TR.Co (3.3) 表示电容Cgs形成的极点频率，Rs是电容Cgs看到的电阻，更精确地，为RsR12。如 果考虑R12,则输出阻抗为 乙==R2lsC。=1+Rc,5 尺2 (3.4) (2)只考虑电容Cds 这时增益的表达式与式(3.1)相似，只不过极点变为 1 2TRCas (3.5) 表示电容Cs形成的极点频率，其中R是电容Cs看到的电阻， R=Rll rds 3.6) 输出阻抗为 Vout= Zout= R (3.7) lout 1+jf/f2 (3)只考虑电容Cgd 电容Cg非常重要，作为从输出节点到输入节点的反馈电容，它使得从输出节点和输入 极点看到的电容增大了。 增益为 1-jf /fo Ay Av0 1+jflfea (3.8) 其中 12

单管和双管放大器的频响分析 12 3.1.1 单独考虑各个电容 我们先单独考虑各个电容对频率响应特性的影响。 (1) 只考虑电容 Cgs 很容易可以求出增益为   v0 v 1 c1 A A jf f (3.1) 其中   ' A g R v0 m L (3.2) 表示低频增益； c1  s gs 1 2π f R C (3.3) 表示电容 Cgs 形成的极点频率，RS 是电容 Cgs 看到的电阻，更精确地，为 RS||R12。如 果考虑 R12，则输出阻抗为     in 12 in 12 gs in 12 gs 1 v R Z R sC i R C s (3.4) (2) 只考虑电容 Cds 这时增益的表达式与式 (3.1) 相似，只不过极点变为 c2  ' L ds 1 2π f R C (3.5) 表示电容 Cds 形成的极点频率，其中 ' RL 是电容 Cds 看到的电阻,  ' R R r L L ds (3.6) 输出阻抗为    ' out L out out c2 1 v R Z i jf f (3.7) (3) 只考虑电容 Cgd 电容 Cgd非常重要，作为从输出节点到输入节点的反馈电容，它使得从输出节点和输入 极点看到的电容增大了。 增益为    c4 V V0 c3 1 / 1 / jf f A A jf f (3.8) 其中

第三章单管放大器的频率响应特性 f=2TTMRsCo (3.9) M=1+尽+gR=1+尽-A0 (3.10) R. R 64。9m 2TCgd (3.11) 增益传输函数包含一个极点f3和一个零点f4,在低频时，显然A=Avo;因为极点f3 中的M因子（代表Miller效应）包含Avo,通常较大，在高频时，极点往往占主导地位， 即极点频率更低。 密勒效应(Miller效应) 值得注意的是，现在截止频率f3不是简单地由RC,而是由MRC决定的，因子M 加进了RC积。M是与低频增益绝对值成正比的系数，反映了反馈电容对输入节点时间 常数的影响程度。因子M中的最大的一项是低频增益A0,当低频增益足够大时，可以 近似为M=1-Avo即Miller因子。主极点是倍增的电容Cgd(乘以放大级低频增益)和源 电阻Rs的乘积造成的。可以等效成输入节点有一个电容C,它的值为 Ca=MCa≈AvoCgd (3.12) 这称为Miller效应，Ca称为Miller电容 在更高频率上，式(3.9)给出的零点出现，零点的大小为f4。超过该频率，增益的 频率响应将会变得平坦，而且达到纯电阻性的Ah。由式(3.9)容易算出 A质R (3.13) 由图3-2容易看出，在绝对值上比例f4/fc3和Avo/Avh相等。实际上，频率f3和f4之间 的斜率等于1或者说是-20dB/decade。 除去偏置电阻，只考虑电容时的输入阻抗为 1 in 1+RCodS 1 1-A0 (3.14) CgdS ≈MCgs 其中，零点为 1 fes=2TRCod (3.15) 这表示在低频处，输入端看到的电容为Miller电容。在高于f6的频率，式(3.15)中给 出的零点变得更加重要，在这些高频范围，输入阻抗是电阻性的，而且等于R产1/gm。 3

第三章 单管放大器的频率响应特性 13 c3  S gd 1 2πM f R C (3.9)       ' ' L L ' m L v0 s s 1 1 R R M g R A R R (3.10)  m c4 2π gd g f C (3.11) 增益传输函数包含一个极点 fc3 和一个零点 fc4，在低频时，显然|AV|=AV0；因为极点 fc3 中的 M 因子（代表 Miller 效应）包含 AV0，通常较大，在高频时，极点往往占主导地位， 即极点频率更低。 密勒效应 (Miller 效应) 值得注意的是，现在截止频率 fc3不是简单地由 RC，而是由 MRC 决定的，因子 M 加进了 RC 积。M 是与低频增益绝对值成正比的系数，反映了反馈电容对输入节点时间 常数的影响程度。因子 M 中的最大的一项是低频增益 AV0，当低频增益足够大时，可以 近似为 M=1-AV0即 Miller 因子。主极点是倍增的电容 Cgd（乘以放大级低频增益）和源 电阻 RS的乘积造成的。可以等效成输入节点有一个电容 ' Cgd ，它的值为   ' C MC A C gd gd V0 gd (3.12) 这称为 Miller 效应， ' Cgd 称为 Miller 电容 在更高频率上，式 (3.9) 给出的零点出现，零点的大小为 fc4。超过该频率，增益的 频率响应将会变得平坦，而且达到纯电阻性的 AVh。由式 (3.9) 容易算出   ' L vh s m s R 1 A MR g R (3.13) 由图 3-2 容易看出，在绝对值上比例 fc4/fc3和 AV0/AVh相等。实际上，频率 fc3和 fc4之间 的斜率等于 1 或者说是-20dB/decade。 除去偏置电阻，只考虑电容时的输入阻抗为           ' L gd in v0 gd gd 1 1 1 1 R C s Z A C s MC (3.14) 其中，零点为 c5  ' L gd 1 2π f R C (3.15) 这表示在低频处，输入端看到的电容为 Miller 电容。在高于 fc6的频率，式 (3.15) 中给 出的零点变得更加重要，在这些高频范围，输入阻抗是电阻性的，而且等于 Rin≈1/gm

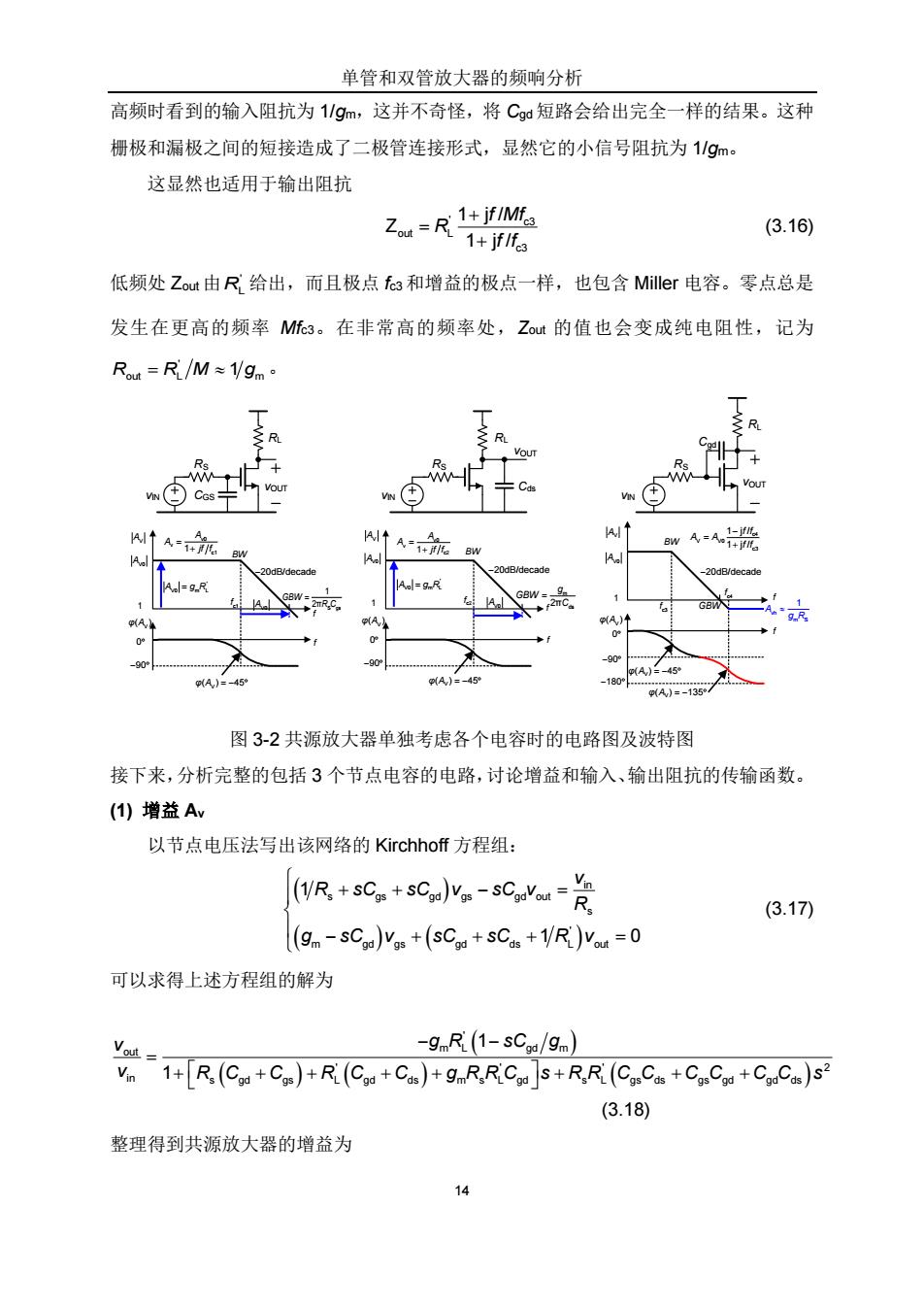
单管和双管放大器的频响分析 高频时看到的输入阻抗为1/gm,这并不奇怪，将Cgd短路会给出完全一样的结果。这种 栅极和漏极之间的短接造成了二极管连接形式，显然它的小信号阻抗为1/gm。 这显然也适用于输出阻抗 2R院 (3.16) 低频处Zout由R给出，而且极点f3和增益的极点一样，也包含Miller电容。零点总是 发生在更高的频率M3。在非常高的频率处，Zout的值也会变成纯电阻性，记为 Rut=R/M≈1/gm R VoUT Rs M 二Cd VIN A A 1-j A=1+ A1+ 20dB/decade -20dB/decade -20dB/decade l=g.R GBW= TR.C A GBW (A) A)↑ 0 -90° -909 p(A)=-45 (A)=-45 A)=-45 -180°. (A)=-135° 图32共源放大器单独考虑各个电容时的电路图及波特图 接下来，分析完整的包括3个节点电容的电路，讨论增益和输入、输出阻抗的传输函数。 (1)增益Av 以节点电压法写出该网络的Kirchhoff方程组： (WR+sCs+sCpy。-sCYu- R (3.17) (9m-SCgd)Vgs +(SCgd+SCas +1R)Vout =0 可以求得上述方程组的解为 Vt一 -gnR(1-sCa/9m） Vin 1+Ra(Cod+Cos)+RL(Cod+Cus)+gmRRCodS+RRL(CgsCas +CgsCod+CgdCds)s2 (3.18) 整理得到共源放大器的增益为 14

单管和双管放大器的频响分析 14 高频时看到的输入阻抗为 1/gm，这并不奇怪，将 Cgd短路会给出完全一样的结果。这种 栅极和漏极之间的短接造成了二极管连接形式，显然它的小信号阻抗为 1/gm。 这显然也适用于输出阻抗    ' c3 out L c3 1 j / Z 1 j / f Mf R f f (3.16) 低频处 Zout 由 ' RL 给出，而且极点 fc3 和增益的极点一样，也包含 Miller 电容。零点总是 发生在更高的频率 Mfc3。在非常高的频率处，Zout 的值也会变成纯电阻性，记为   ' R R M g out L m 1 。 图 3-2 共源放大器单独考虑各个电容时的电路图及波特图 接下来，分析完整的包括 3 个节点电容的电路，讨论增益和输入、输出阻抗的传输函数。 (1) 增益 Av 以节点电压法写出该网络的 Kirchhoff 方程组：                     in s gs gd gs gd out s ' m gd gs gd ds L out 1 1 0 v R sC sC v sC v R g sC v sC sC R v (3.17) 可以求得上述方程组的解为                        ' out m L gd m ' ' ' 2 in s gd gs L gd ds m s L gd s L gs ds gs gd gd ds 1 1 v g R sC g v R C C R C C g R R C s R R C C C C C C s (3.18) 整理得到共源放大器的增益为 AV  ' A g R V0 m L AV0 BW  m ds 2π g GBW C   900 V φ( ) A 1 c2 f 20dB/decade AV0    V φ( ) 45 A f f  ' A g R V0 m L AV AV0 BW  S gs 1 2π GBW R C   900 V φ( ) A 1 c1 f 20dB/decade AV0    V φ( ) 45 A f f AV AV0 BW GBW   900 V φ( ) A 1 c3 f 20dB/decade    V φ( ) 45 A f f   180 c4 f vh  m S 1 A g R    V φ( ) 135 A vOUT vIN RL RS CGS vOUT vIN RS Cgd vIN RL RS vOUT Cds RL   v0 v 1 c1 A A jf f   v0 v 1 c2 A A jf f    c4 V V0 c3 1 j / 1 j / f f A A f f

第三章单管放大器的频率响应特性 1-sCg的/9m R.(CMC)+RRCs (3.19) Vin 其中 C2=CgsCds+CgsCgd+CpdCds (3.20) (2)输入阻抗Zn 为求电路网络的输入阻抗，在输入端加一个电流源作为激励，然后求出输入端的 电压g即可。设在输入端加一个电流为加的电流源，运用节点电压法可以得到下列 Kirchhoff方程组 (SCgs+SCgd)Vg-SCodVout in (3.21) -SCgdVg+(SCgd+SCds+1/R)Vout =0 可以求得上述方程组的解为 1+RL(Cgd+Cas)s InCy+(1+gR)Cos+R(CnCu+CuCo+CoCo)s (3.22) 所以输入阻抗为 1+R(Cgd+Cos)s Z,[C+0+gR)0s1 (3.23) RC2s2 「Cs+(1+gnR)cgas 即 1+R(Cga+Cds)s Z.G,+0-A0,51+Ce+-AcF RC2s2 (3.24) 其中 1 (3.25) 2TR(Cg+Cas） (3)输出阻抗Zout 为求电路网络的输出阻抗，在输出端加一个电流源ot作为激励，然后求出输出端 的电压Vou即可。当分析带有激励信号源的网络的输出阻抗时，应将激励源去除之后再 求输出阻抗。原则是：电压源短路，电流源开路，同时全部保留它们的源内阻。 将图中激励电压源短路，在输出端加激励电流iout,运用节点电压法可以得到下 列Kirchhoff方程组 15

第三章 单管放大器的频率响应特性 15              out gd m v v0 ' ' 2 2 in s gs gd L ds s L 1 1 v sC g A A v R C MC R C s R R C s (3.19) 其中    2 C C C C C C C gs ds gs gd gd ds (3.20) (2) 输入阻抗 Zin 为求电路网络的输入阻抗，在输入端加一个电流源 iin作为激励，然后求出输入端的 电压 vg 即可。设在输入端加一个电流为 iin 的电流源，运用节点电压法可以得到下列 Kirchhoff 方程组                 gs gd g gd out in ' gd g gd ds L out 1 0 sC sC v sC v i sC v sC sC R v (3.21) 可以求得上述方程组的解为                   ' g L gd ds ' ' 2 in gs m L gd L gs ds gs gd gd ds 1 1 v R C C s i C g R C s R C C C C C C s (3.22) 所以输入阻抗为                       ' L gd ds in ' ' 2 2 gs m L gd L ' gs m L gd 1 1 1 1 1 R C C s Z C g R C s R C s C g R C s (3.23) 即                       ' L gd ds in ' 2 2 gs v0 gd L gs v0 gd 1 1 1 1 1 R C C s Z C A C s R C s C A C s (3.24) 其中     c16 ' L gd ds 1 2π f R C C (3.25) (3) 输出阻抗 Zout 为求电路网络的输出阻抗，在输出端加一个电流源 iout 作为激励，然后求出输出端 的电压 vout 即可。当分析带有激励信号源的网络的输出阻抗时，应将激励源去除之后再 求输出阻抗。原则是：电压源短路，电流源开路，同时全部保留它们的源内阻。 将图中激励电压源 vin短路，在输出端加激励电流 iout，运用节点电压法可以得到下 列 Kirchhoff 方程组