
22 第一章热力学基础 比等温线的斜率更陡 下面将证明,这个结论不仅对理想气体成立,而且对更一般的任何具有两个 独立参量的体系也都成立.的确,对绝热过程,由第一定律 dQ=dU+pdv=0, 由(1.4.13)及(1.4.15)式得 CdT+(C,-C)(0),dv=0. (1.5.15) 利用 ar=(3.p+(0).av, 改换独立变量,使独立变量由(1.5.15)式的(T,V)换为(p,V),得 c[(g6)p+().av]+(c,-c)(0),av=0.(15.16 即 c.(3)dp+C.()dv-0. (1.5.17) 现在来证明一个非常有用的数学公式,设x、y、之满足函数关系 f(x,y,z)=0 则由 afdx+y df=a afdz=0. 得 aflax 相乘后得 ).()(,=-1, (1.5.18) 利用微商关系(1.5.18),得 0.().()。=-1. (1.5.19) 由(1.5.17)和(1.5.19)式,最后得出 (1.5.20) §1.6理想气体的卡诺循环过程 历史上,在生产实践中具有重要意义的是热机.热力学在历史上是从研究和
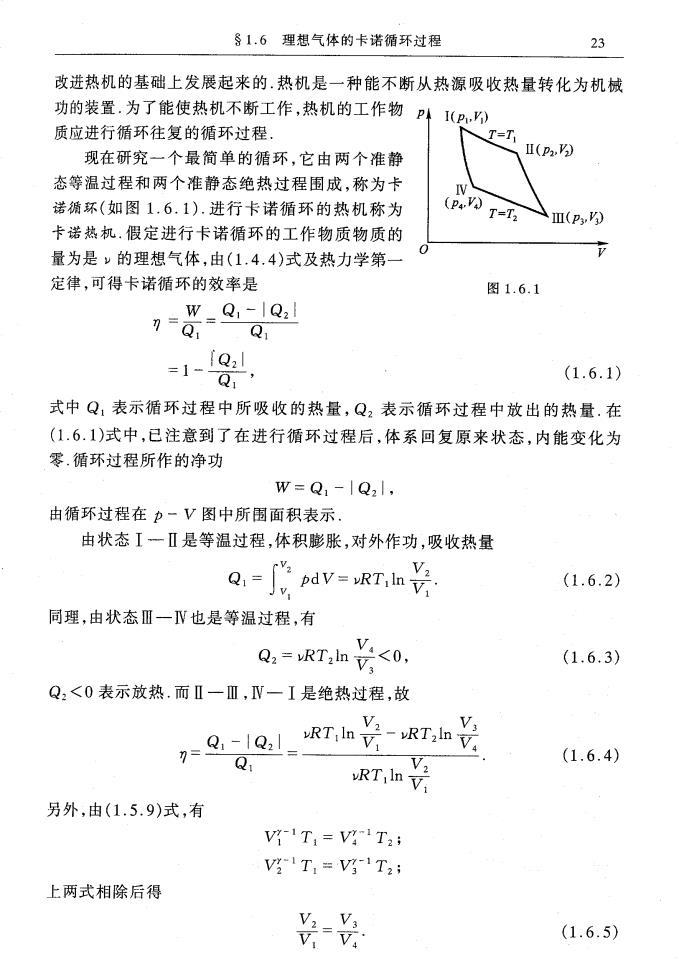
§1.6理想气体的卡诺循环过程 23 改进热机的基础上发展起来的,热机是一种能不断从热源吸收热量转化为机械 功的装置.为了能使热机不断工作,热机的工作物P4 I(P,) 质应进行循环往复的循环过程. T=T 现在研究一个最简单的循环,它由两个准静 Ⅱ(P2,) 态等温过程和两个准静态绝热过程围成,称为卡 诺循环(如图1.6.1).进行卡诺循环的热机称为 (P4) T=T2 Ⅲ(P,) 卡诺热机.假定进行卡诺循环的工作物质物质的 量为是的理想气体,由(1.4.4)式及热力学第一 定律,可得卡诺循环的效率是 图1.6.1 W-Q,-|Q2 Q =1-fQ1 Q (1.6.1) 式中Q,表示循环过程中所吸收的热量,Q2表示循环过程中放出的热量.在 (1.6.1)式中,已注意到了在进行循环过程后,体系回复原来状态,内能变化为 零.循环过程所作的净功 w=Q1-|Q21, 由循环过程在p-V图中所围面积表示. 由状态I一Ⅱ是等温过程,体积膨胀,对外作功,吸收热量 Q,=Jdv=RTh长 (1.6.2) 同理,由状态Ⅲ一Ⅳ也是等温过程,有 Q:=kT,h长<0, (1.6.3) Q2<0表示放热.而Ⅱ一Ⅲ,V一I是绝热过程,故 V2 7=9-1Q1 RTiIn V -yRTaln V Q (1.6.4) RTiln Vi 另外,由(1.5.9)式,有 V7-1T1=Vg1T2; V-ITI=V3T2i 上两式相除后得 (1.6.5)

24 第一章热力学基础 将(1.6.5)式代入(1.6.4)式后得 T2 0=1- (1.6.6) (1.6.6)表明,以理想气体为工作物质的准静态卡诺热机的效率只与热源和冷源 的温度有关.而与p一V图中,卡诺循环包围的面积无关.卡诺循环包围的面积 越大,吸热也越多,WQ,仍然不变 §1.7热力学第二定律 在自然界中,违反热力学第一定律的过程是不能实现的.但是,不违反热力 学第一定律的过程是否全部都能够实现呢?日常生活的经验告诉我们,答案是 否定的.例如,让两个不同温度的物体互相接触,并使这两个物体和外界隔绝,这 两个物体进行热交换的结果总是高温物体温度下降,低温物体的温度上升,最后 两个物体达到相同的温度,从未发生过高温物体温度上升,低温物体温度下降, 两个物体之间温度相差越来越大的情况.尽管后者只要低温物体失去的热量等 于高温物体获得的热量,也同样满足热力学第一定律.在使重物的下落以带动叶 轮,再让叶轮搅动容器中的水,使水温度升高的焦耳热功当量的实验里,实验规 察到的也只是重物所作的功转化为热,也从来没有发现过作为热源的水自动冷 却而使重物上升的情况,虽然在这种情况下,只要热源冷却过程中放出的热量等 于重物上升时所消耗的功,也同样不违背热力学第一定律.这些例子说明,自然 界中必然还存在不同于热力学第一定律的其它规律,制约着自然过程的发展.这 个规律排除了某些不违背热力学第一定律的过程出现的可能性 实际上,自然界内任何宏观自发过程都具有方向性.自发过程是指在不受外 来干预的条件下体系自发进行的过程,对于孤立系,根据热力学平衡的实验,过 程自发发展的方向总是从非平衡态到平衡态,不能在外界对体系既不作功,又不 交换热量,即不加外来作用的条件下自发地从平衡态过渡到非平衡态.在热力学 中,所谓过程的方向总是指过程自发进行的方向.任何过程,加上外来的干预后, 方向就毫无意义了.例如,如果用一部制冷机工作在低温物体和高温物体之间, 通过外界作功,完全可以使热量从低温物体传到高温物体中去,从而使低温物体 温度下降,高温物体温度上升,这就谈不上热传导过程的方向性 这里要指出:过程自发进行的方向性的问题在历史上是和如何提高热机效 率的问题紧密相联系的.按热力学第一定律,热机效率?不大于1.但?可否等 于1呢?由(1.6.1)式,7=1即Q2=0,它不放热,卡诺循环中的热源T2完全 不起作用.这是一种只有一个热源的机器,它从单一热源吸取热量全部用来对外 作功,而且,除对外作功外,不引起其它变化.体系和外界都回到了原来状态.这

§1.7热力学第二定律 25 种过程是否可以实现是和热和功之间转化的方向性问题联系在一起的 可逆过程热力学第二定律是关于自发过程方向性的定律.为把过程的方 向性明确化,在物理学中常引进可逆过程的概念,在自发过程中,从非平衡态过 渡到平衡态的正过程和破坏平衡态,使它回复到原来非平衡态的逆过程是不等 当的.前者是自发的,后者却必须有外来作用,或者说,必然伴随有外界的变化 因此定义:一个过程,如果每一步都可在相反的方向进行而不引起外界的其它任 何变化,则称此过程为可逆过程,反之,即为不可逆过程 现在对可逆过程的概念作一些讨论: ()所谓一个过程不可逆,并不是说一个不可逆过程的逆过程不能进行,而 是说当过程逆向进行时,逆过程在外界留下的痕迹不能将原来正过程的痕迹消 去.可逆过程定义的关键之处在于“不引起外界的其它任何变化”这句话.它的含 意是:正过程和逆过程合起来后总的后果是:体系复原,外界复原,正过程在任何 地方留下的痕迹都能被逆过程在同一地方留下的痕迹消去,而使总的后果为零, 同样,所谓一个过程可逆,也并不是说一个过程可以自发地自动逆向进行,逆向 进行的过程不会是自发的,必须依靠外来作用才能使过程逆向进行.但是,可逆 过程是说,如果它逆向进行的话,则其逆过程与正过程的一切痕迹消去 ()一切自发过程都是不可逆的,我们说宏观自发过程是不可逆过程,但这 并不是说人为控制的不是自发的过程就都是可逆过程,人为控制的过程既可能 是可逆的,也可能是不可逆的.设想一个装有气体的气缸,如果把气缸的活塞很 快地拉动,这个非静态过程就是个不可逆过程.当活塞向外拉动时,由于拉动速 度很快,气体分子还来不及全部跟随活塞运动.这样,靠近活塞的气体较稀薄,内 部的气体较稠密.而在逆过程中,即将活塞向内压缩时,情况则相反.靠近活塞的 气体较稠密,内部的气体较稀薄.因此,正过程和逆过程的痕迹不能消去,总的后 果必然在外界留下影响 ()那么,什么过程是可逆的呢?要使过程可逆,必须使正过程和逆过程 中相应的态具有相同的参量换句话说,必须使过程在反向进行时,每一步都是 正过程相应的一步的重复.也就是说,这个过程在时间反演t一t时具有不变 性.因为在当t→一t时,正过程变成了逆过程.在热力学中,这只有在准静态无 摩擦的条件下才有可能.因为对于准静态过程,过程中的每一一步,体系都处在平 衡态.不管是正行还是逆行,只要达到这个平衡态,参量都具有同样的确定的数 值,又因为是无摩擦的,体系的压强和外界的压强在任何时刻都具有相同的数 值,因而正过程和逆过程所作的功大小相等,符号相反,总的后果为零.这说明, 对于无摩擦的准静态过程,当反向进行时,物体和外界在过程中的每-一步的状态 都是原来正过程的重复,因此是可逆过程,以后在本书中,如不特别指明,都略去 摩擦力,因而可认为准静态过程就是可逆过程

26 第一章热力学基础 (v)事实上,自然界中的各种不可逆过程是相互联系的.可以从一个过程 的不可逆性推断另一个过程的不可逆性.例如可以从热传导过程的不可逆性推 断摩擦生热过程的不可逆性,也可以反过来.因为总可以通过各种设计把不同过 程联系起来,(请读者自己设计一种方案,以论证若热传导过程不可逆,则摩擦生 热过程必不可逆.)同样还可以证实,一个不可逆过程,不仅在直接反向进行时不 能消除外界的所有影响,而且无论用任何曲折复杂的方法,也都不可能使体系和 外界都完全恢复原状,不引起其它变化,消除所有影响 (ν)既然一个不可逆过程无论用任何方法都不能使体系和外界都恢复原状 而不引起任何变化,因此一个过程的不可逆性与其说是决定于过程本身,毋宁说 决定于它的初态和未态.在自发的,即不加外来影响的条件下,不可逆过程的初、 末态是不等当的.例如对孤立系所进行的弛豫过程,体系可以自发地从初态(非 平衡态)变到末态(平衡态),但却不能自发地从末态变到初态.初态是非平衡态, 末态是平衡态,这种不等当性就决定了弛豫过程一定是不可逆过程.由于这种 初、末态的不等当性,必然存在一个仅和初态、末态有关而与过程无关的态函数, 可以用它来判别自发过程进行的方向,这个态函数就是熵.热力学第二定律,就 是把这种自发过程的方向性抽象出来,提高到基本定律的地位;就是要找出这个 态函数熵来,用它明确规定自发过程的不可逆性 热力学第二定律热力学第二定律是关于自发过程方向性的规律,它明确 指出了某些过程的不可逆性,它是大量实验事实的总结,由于自然界中不可逆过 程是多种多样的,因而热力学第二定律也有多种不同的表述形式: (a)克劳修斯(Clausius)说法:不可能把热量从低温物体传给高温物体而不 引起其它变化 (b)开尔文(Kelvin)说法:不可能从单一热源吸收热量使它完全变成有用的 功而不产生其它影响 (c)普朗克(Planck)说法:不可能制造一部机器,在循环动作中把一重物升 高而同时使一热库冷却 这里要特别强调指出,在所有这些说法中,“不引起其它变化”、“不产生其它 影响”、“循环动作”等条件是极为重要的.这些条件,本质上就是说的“不可逆 性”.离开了这些条件,当然可以使热量从低温热源传给高温热源,例如只要用制 冷机在其中工作,通过外界对体系作功就可以做到这一点.也可以从单一热源吸 取热量使它全部变成功,比如理想气体作等温膨胀,这个过程内能不变,吸收的 热量就全部变为功,但结果是体系体积变大了,外界体积缩小了,过程进行的后 果在外界留下了影响.事实上,克劳修斯说法实质上是说热传导过程的不可逆 性.开尔文说法、普朗克说法实质上指的是热和功之间的转换,比方摩擦生热过 程的不可逆性