
S1.4热力学第一定律 17 比热容.在一定条件下,物体温度升高1K时所吸收的热量称为热容.热容是广 延量.而把单位质量的热容称为比热容.热容C,和比热容℃.的数学表示式分别 是 c=(会9).=() (1.4.6) (1.4.7) m是物体的质量,脚标x表示相应的过程,因为àQ与过程有关,所以热容和比 热容都与过程有关.比热容是强度量,由(1.4.6)式可见,绝热过程的热容为零, 而等温过程的热容趋于无限大。 现在来求定压过程的热容C。和定容过程的热容Cv.取只有两个独立参量 的体系,比如化学纯的气体,在准静态过程中,由热力学第一定律 aQ=dU+pdv, 得 c=(),=(.: (1.4.8) c,=()=(),+p),: (1.4.9) 注意(1.4.8)式对非静态过程也适用,因为只要是等容过程,功总为零.但(1.4. 9)式只适用于准静态过程或非静态但外界等压的过程 如果要把(1.4.9)式也写成类似于(1.4.8)式的形式,可以将独立变量从 (T,V)换成(T,p).引入 H=U+bV, (1.4.10) H称为焓,显然H也是态函数.对(1.4.10)式两端微分, dH=dU+pdv+Vdp=aQ+Vdp, a C,=(aT, (1.4.11) (1.4.11)式表明,在准静态等压过程中,体系焓的增量等于它所吸收的热量。 分别以(p,V)、(V,T)和(p,T)为独立变量,用(1.4.8)式和(1.4.9)式,可 将热量dQ表示为: dQ=(g),p+[(),+p]av. (1.4.12) aQ=(),ar+[(g0),+p]av =cdr+[(0),+p]av, (1.4.13)

18 第一章热力学基础 aQ= (3).ar+(g),p+p[),dr+(影),p] =c,dr+[(g),+p(3%),]ap: (1.4.14) 在热力学意义下,热容由实验测量得出,在统计物理学中,在引进一些模型和假 设之后,热容可由理论推出。 定压热容和定容热容之间的关系可由(1.4.13)、(1.4.14)式得出,在等压条 件下比较这两式,得 c,=c+[(),+]Y)。 (1.4.15) 通常,在热力学意义下,只要把U、H等热力学函数归结为C。、Cv和状态 方程等可从实验测得的量,就可认为问题已经解决,因为热力学是一种宏观理 论,它从实验出发,归纳为一些基本定律,然后经过演绎推理,解释物质在不同过 程和状态中更多的新的性质,再把这些性质在实验中检验.因此只要把一些物理 量如U、H等归结为C。、Cv或压强p、体积V、温度T等实验上可以直接测量 的物理量后,就可以准确到一个待定常数(如U。),从实验上给出这些态函数. 例如内能,取U=U(T,V),由(1.4.8)式及(1.4.15)式,有 au=(),ar+(0),dv =cvdr+[(C,-c)(0),-b]av, (1.4.16) 可由状态方程求得 利用(1.4.16)式,可以求得理想气体的定压热容与定容热容之差C。-Cv. 对于理想气体,它向真空自由膨胀的焦耳(Joule)实验表明,气体膨胀前后的 温度不变这说明,理想气体的内能仪仅是温度的函数,而与体积无关,因为向真 空自由膨胀的过程中,外压强po为零,由(1.4.5)式,得△W=0.另外,向真空自 由膨胀过程中,气体膨胀得很快,过程可视为是绝热进行的,亦即△Q=0.由热 力学第一定律得,△U=0.气体膨胀前后的初态和末态具有相同的内能、相同的 温度,但不同的体积.因此有 =0, (1.4.17) dU=CvdT. (1.4.18) 在温区不太大的情况下,可认为Cv是常数,从而得 U=CvT+Uo. (1.4.19)

§1.5理想气体的多方过程 19 不失普遍性,可选积分常数U。=0,由 H=U+pV=CvT+pV=(Cv+vR)T, (1.4.20) 式中y为理想气体的物质的量,得 (aH C=aT。 =Cy+R, 或写成 C-Cv=vR. (1.4.21) (1.4.22)式也可由(1.4.16)及(1.4.18)式得出.的确,由 0),=(c,-C)(0,-=0 (1.4.22) 及理想气体的状态方程,V=RT,得 a av =R, (1.4.23) 代入(1.4.23)式后,亦可得(1.4.22)式 §1.5理想气体的多方过程 利用理想气体的状态方程V=RT及内能仅是温度函数的结论,本节将 计算一些重要的物理过程中理想气体所作的功、内能的变化和热量,但是应该指 出,对理想气体说来,状态方程和 0), =0并非两个独立的结果,以后将证明, 由状态方程可导出(),=0.事实上,从微观上看,(】 =0的结论也是易 于理解的.因为体积变化,只改变分子之间的距离,从而改变它们的相互作用能. 而对于理想气体,分子之间的距离较大,比分子的直径大一个数量级以上,分子 之间的相互作用能本来就远远小于分子的无规则运动的平均动能,这部分相互 作用能本来就已经被忽略.而体积膨胀又不影响气体分子的平均动能.因此,理 想气体的内能不因体积的改变而改变。 定义热容C为常数的过程为多方过程,对于理想气体,由热力学第一定律 aQ=CydT+pdv, (1.5.1) 另一方面,按多方过程的定义 aQ=CdT. (1.5.2) 由(1.5.1)、(1.5.2)式有 CdT=CydT+pdV; (1.5.3) 由状态方程得

20 第一章热力学基础 pdV+Vdp=vRdT. (1.5.4) 在(1.5.3)、(1.5.4)式中消去dT,再注意到C。-Cv=R,得 C,-CdV+dp=0, Cv-CV (1.5.5) 积分后得 pV"=const. (1.5.6) 其中”=称为多方指数.(1.5.6)式是多方过程所满足的方程式.由于密 度p=,N是气体的分子数,(1.56)也可写成 po"=const. (1.5.7) 在多方过程中,压强与密度ρ的n次幂成正比.多方过程对天体物理学中脉冲 星等致密星体的讨论是非常重要的. 考察理想气体多方过程的几个特殊情况: (i)绝热过程 dQ=0.C=0,n=名=7 (1.5.6)式变为: pV7 const. (1.5.8) (1.5.8)称为泊松(Poisson)方程,它也可以改写成用(T,V)及(T,p)表示的形 式.把(1.5.8)式与状态方程联立,得 TV?-=const. (1.5.9) 或 p-YTY=const. (1.5.10) 另外,由热力学第一定律,有 dU+aW=CvdT+pdV=0. (i)等温过程 dT=0, 由于理想气体内能仅是温度的函数,有 dU=0, 又因一般说来,准静态等温过程并不绝热,即 dQ丰0 故有 C→∞,n→1, V=const. (1.5.11) aQ=pdv
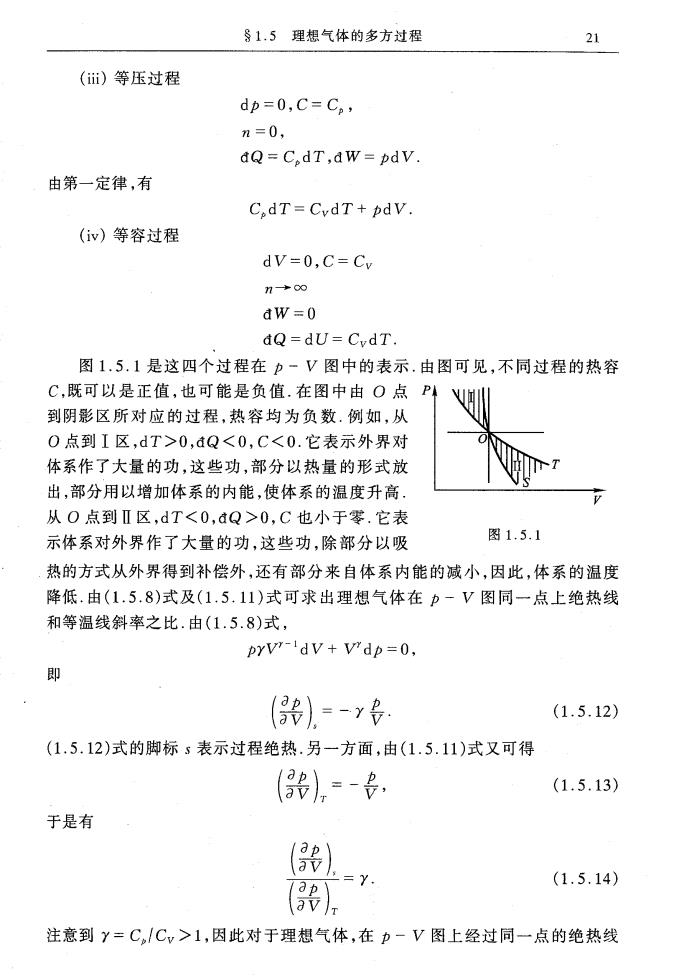
§1.5理想气体的多方过程 21 ()等压过程 dp=0,C=C。, n=0, dQ=C,dT,aw=pdV. 由第一定律,有 C.dT=CydT+pdV. (iv)等容过程 dV=0,C=Cv no dw=0 dQ=dU=CvdT. 图1.5.1是这四个过程在p~V图中的表示.由图可见,不同过程的热容 C,既可以是正值,也可能是负值.在图中由O点P 到阴影区所对应的过程,热容均为负数.例如,从 0点到I区,dT>0,dQ<0,C<0.它表示外界对 体系作了大量的功,这些功,部分以热量的形式放 出,部分用以增加体系的内能,使体系的温度升高. 从O点到Ⅱ区,dT<0,dQ>0,C也小于零.它表 示体系对外界作了大量的功,这些功,除部分以吸 图1.5.1 热的方式从外界得到补偿外,还有部分来自体系内能的减小,因此,体系的温度 降低.由(1.5.8)式及(1.5.11)式可求出理想气体在力-V图同一点上绝热线 和等温线斜率之比.由(1.5.8)式, prV-dv+v'dp=0, 即 (器)=-y (1.5.12) (1.5.12)式的脚标s表示过程绝热.另一方面,由(1.5.11)式又可得 0),=- (1.5.13) 于是有 p av). (1.5.14) av 注意到Y=C,/Cv>1,因此对于理想气体,在p-V图上经过同一点的绝热线