
6.4 Hartree-Fock-Roothaan六程 FC=SCa C11 C12 … C1K C= C21 C22 … C2K 系数矩阵 … CK1 CK2 CKK 0 0 0 82 0 8= HF问题转变为矩阵方程问题 0 0 d)-ab 其中 N/2 (wo)=∬.(1点()g4(2)4(2)drd, Puv=2∑cca 密度矩阵元 PS矩阵 对角元 PSμ-原子轨道9u上的电子布局 非对角元 PvSw-原子轨道ppv之间的电子密度布局
LCAO-MO 16 Chapter 6 HF 6.4 Hartree-Fock-Roothaan方程
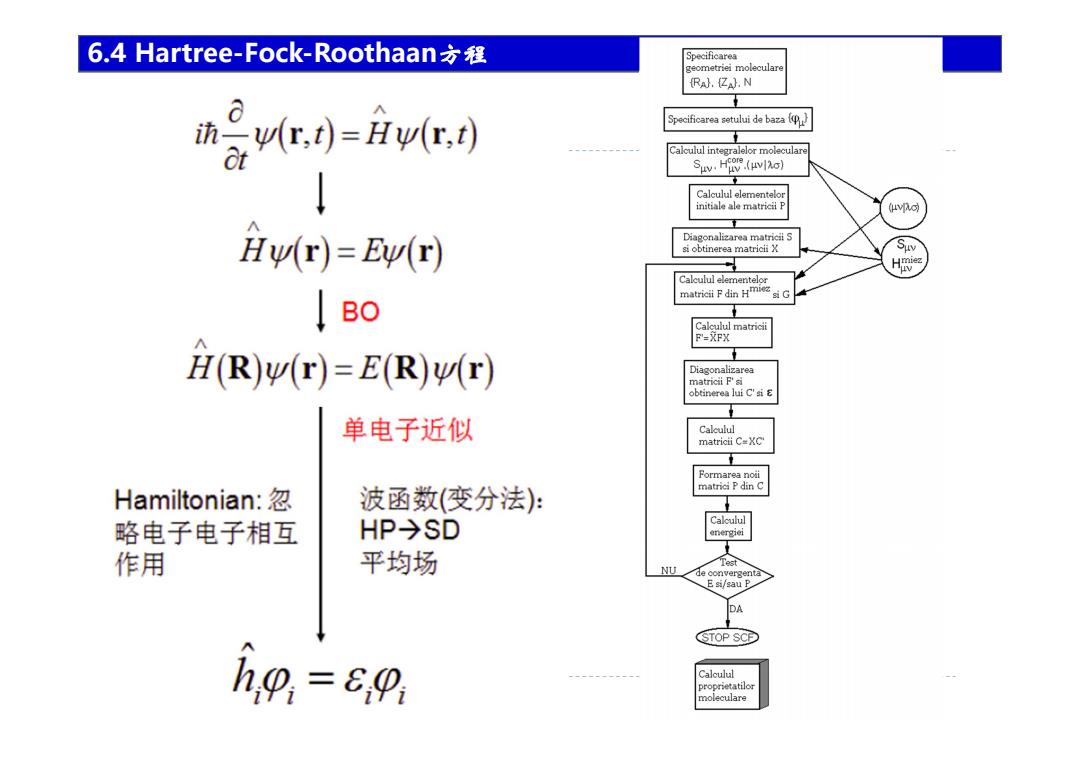
6.4 Hartree-Fock-Roothaan六程 Specificarea geometriei moleculare R.亿.N 经c=ve Specificarea stului de baa Calculul integralelor moleculare Suv.Hw.(μw2oj Calculul elementelor initiale ale matricii P v Hv(r)=E(r) Diagonalizarea matricii S si obtinerea matricii X H2 Calculul elementelor |B0 matricii Fdin Hmie Calculul matricii F-XFX H(R)v(r)=E(R)w(r) Diagonalizarea matricii F'si obtinerea lui C'si E 单电子近似 Caleulul matricii C=XC Formarea noii matrici P din C Hamiltonian:忽 波函数(变分法): Calculul 略电子电子相互 HP→SD ner它i 作用 平均场 Test NU de convergenta E si/sau P DA STOP SCP h,0,=e0 Caleulul proprietatilor moleculare
LCAO-MO 17 Chapter 6 HF 6.4 Hartree-Fock-Roothaan方程

6.4 Hartree-Fock-Roothaan方程 Restricted or Unrestricted HF Restricted HF restricted wave-function ④1(x)=p1(r)a(w)④2(x)=p1(r)p(w) |YF)=p,p2s} Restricted wave-function for Li atom But:Kis()2s)0 and Kis(p)2s()=0 1s(a)and 1s(B)electrons will experience different potentials so that it will be more convenient to describe the two kind of electrons by different wave-functions Unrestricted HF-No restriction on spatial wavefunction for spin orbit Φ(×)=p1(r)a(w)重2(×)=p1(r)B(w) 十一% 出)=醒p》 Unrestricted wave-function for Li atom op〉=δg(gg〉=6(ale}=sg >18 Chapter 6 HF
Restricted or Unrestricted HF 18 Chapter 6 HF 6.4 Hartree-Fock-Roothaan方程

6.5基组 STO 对分子体系进行从头计算时,分子轨道要用一套基函数(基 组)展开,常用基组包括 (1)STO (Slater Type Orbitals) om(r5)=R(r5)Y(0.2) Ru=rm-lesr 有时也有几个径向函数线性组合来近似一个原子轨道 R=2c,R,(G,5) R,(r,5)=r-e 对应n=1,2,3称为单(,双(或三型基组,即SZ,DZ,TZ,这种轨道较接近 原子轨,但计算困难,所以较多用于原子体系及双原子分子体系和半经验计算方 法(此种方法忽略了许多多中心积分),但多原子体系,由于Roothaani方程中 出现许多四中心(双电子)积分。 >19 Chapter 6 HF
STO 19 Chapter 6 HF 6.5 基组 对分子体系进行从头计算时,分子轨道要用一套基函数(基 组)展开,常用基组包括: (1) STO(Slater Type Orbitals) ( , ) ( , ) ( , ) φ n,l,m r ξ = Rn,l r ξ Yl,m θ ϕ n r n l R r e − −ξ = 1 , = = n i n l i i i R c R r 1 , ( ,ξ ) n r i i i R r r e ξ ξ − − = 1 ( , ) 有时也有几个径向函数线性组合来近似一个原子轨道 对应n=1,2,3称为单ζ,双ζ 或三 ζ型基组,即SZ,DZ,TZ,这种轨道较接近 原子轨,但计算困难,所以较多用于原子体系及双原子分子体系和半经验计算方 法(此种方法忽略了许多多中心积分),但多原子体系,由于Roothaan方程中 出现许多四中心(双电子)积分