
第四章分子的对称性与群论基础 … .90 4.1对称元素和对称操作 .90 4.1.1对称元素和对称操作的定义 90 4.1.2对称元素和对称操作的类型 .90 4.2对称操作的乘积、乘法表. 92 4.2.1对称操作的乘积.… …92 4.2.2对称元素和对称操作之间的一般关系 93 4.2.3分子全部对称操作集合的性质乘法表. .94 4.3群的基本概念 95 4.3.1群的定义 95 4.3.2群的几个例子. 95 43.3子群,类和群的同构 96 4.4对称点群 97 4.4.1对称点群 97 4.4.2分子对称性的系统分类法 .99 4.4.3实例. .100 4.5群的表示… .102 4.5.1对称操作的矩阵形式… .102 4.5.2群的表示… 105 4.6群的不可约表示的性质 107 4.6.1“广义正交定理”及其推论 107 4.6.2群的特征标表.… 109 4.6.3可约表示的分解 .111 4.7基函数 112 4.7.】基函数 112 4.7.2对称性匹配的线性组合(SALC)投影算子法. 113 4.8群论和量子力学 115 4.81本征函数是不可约表示的基 .115 4.8.2能级的简并度等于不可约表示的维数 115 4.9群论在化学键和分子力学中的应用 116 4.9.1亲化轨道(Dh对称性). …116 4.9.2休克尔(Huckel)分子轨道(HMO)理论苯分子… 117 4.9.3分子振动H0分子… 118 4.10直乘积表示、分支规则 119 4.10.1直积表示 119 4.10.2对称直积和反称直积 .120 4.10.3选择定则.。 .121 4.10.4分支规则 121 习题 123
1 第四章 分子的对称性与群论基础 ....................................................................................................................... 90 4.1 对称元素和对称操作 .................................................................................................................................... 90 4.1.1 对称元素和对称操作的定义 ............................................................................................................... 90 4.1.2 对称元素和对称操作的类型 ............................................................................................................... 90 4.2 对称操作的乘积、乘法表 .......................................................................................................................... 92 4.2.1 对称操作的乘积 ................................................................................................................................... 92 4.2.2 对称元素和对称操作之间的一般关系 ................................................................................................ 93 4.2.3 分子全部对称操作集合的性质 乘法表 ............................................................................................ 94 4.3 群的基本概念 .............................................................................................................................................. 95 4.3.1 群的定义 ............................................................................................................................................... 95 4.3.2 群的几个例子 ....................................................................................................................................... 95 4.3.3 子群,类和群的同构 ........................................................................................................................... 96 4.4 对称点群 ...................................................................................................................................................... 97 4.4.1 对称点群 ............................................................................................................................................... 97 4.4.2 分子对称性的系统分类法 ................................................................................................................... 99 4.4.3 实例 ..................................................................................................................................................... 100 4.5 群的表示 .................................................................................................................................................... 102 4.5.1 对称操作的矩阵形式 ......................................................................................................................... 102 4.5.2 群的表示 ............................................................................................................................................. 105 4.6 群的不可约表示的性质 ............................................................................................................................ 107 4.6.1 “广义正交定理”及其推论 ............................................................................................................. 107 4.6.2 群的特征标表 ..................................................................................................................................... 109 4.6.3 可约表示的分解 .................................................................................................................................. 111 4.7 基函数 ......................................................................................................................................................... 112 4.7.1 基函数 .................................................................................................................................................. 112 4.7.2 对称性匹配的线性组合(SALC)投影算子法 ...................................................................................... 113 4.8 群论和量子力学 ......................................................................................................................................... 115 4.8.1 本征函数是不可约表示的基 .............................................................................................................. 115 4.8.2 能级的简并度等于不可约表示的维数 ............................................................................................... 115 4.9 群论在化学键和分子力学中的应用 ......................................................................................................... 116 4.9.1 亲化轨道(D3h 对称性).......................................................................................................................... 116 4.9.2 休克尔(Huckel)分子轨道(HMO)理论 苯分子 ........................................................................... 117 4.9.3 分子振动 H2O 分子 .......................................................................................................................... 118 4.10 直乘积表示、分支规则 ........................................................................................................................... 119 4.10.1 直积表示 ............................................................................................................................................ 119 4.10.2 对称直积和反称直积 ....................................................................................................................... 120 4.10.3 选择定则 ........................................................................................................................................... 121 4.10.4 分支规则 ........................................................................................................................................... 121 习题 ..................................................................................................................................................................... 123

第四章 分子的对称性与群论基础 分子的量子力学处理是困难的:我们常常可以从分子的对称性得到有关分子的能级、波函数和分子性 质的定性知识.如象我们在第六章中要看到的一样,分子的对称性或原子周围环境的对称性严格而精确地 决定了一个原子或分子可能具有的能级数目和类型.因此,只要单独从对称性考虑,我们总可以说出问题 的定性特征是什么,不需要任何定量的计算我们就知道有多少能态,在它们之间可能发生哪种相互作用和 跃迁.用另一种方式来说,仅从对称性考虑就可以使我们对“什么是可能的和什么是完全不可能的?”这 个问题给出一个完全而严格的回答。然而,只由对称性考虑不能告诉我们这种可能的事情在实际上发生的 可能性有多大,原则上,对称性可以告诉我们体系的两个状态的能量必然不同,但是,只有经过计算或测 量我们才能决定能量的差别有多大,还有,对称性只能告诉我们在分子的电子光谱或振动光谱中某些吸收 谱带可以发生,但是要知道它们在什么部位发生,强度有多大则需要作计算. 所谓分子的对称性,我们将指核保持固定于其平衡位置所形成的骨架对称性.(对于分子量子力学,我 们的起点将是Borm-Oppenheimer近似,它认为当求解分子的电子波函数时.核是看作固定的,见第七章).应 当注意,一个分子的对称性在不同的电子状态时可能不同,例如HCN在其电子基态时是直线形的,但在某 些激发态时是非直线形的,除非另外指明,我们将只考虑电子基态的对称性,本章由三部分内容组成,第 一部分,4.1-4.4节,是分子的几何对称性和点群,第二部分,4.5-4.7节,介绍了群的表示理论:第三部分, 4.8-4.10节,简述了群论在化学键,分子力学,光谱理论方面的应用, 4.1对称元素和对称操作 为了建立尽可能有用的分子对称性概念,必须制定一些关于对称性的严格数学标准,为此,首先研究 分子可以具有的对称元素的种类,和由这些对称元素所生成的对称操作,下一节将证明,一个分子的全部 对称操作的集合组成一个数学群, 4.1.1对称元素和对称操作的定义 对于对称操作,我们意指一个物体这样的变换,其最后位置与最初位置是物理上不可分辨的,同时物 体中各对点的距离保持不变.例如,考虑平面三角形分子BF3图4.1(),为了方便,我们把其中的氟核标上 号.若我们将分子绕通过硼核并垂直于分子平面的轴逆时针 方向转动120°,新的位置将如图4.1(b)所示.由于事实上氟 核彼此在物理上是不可分辨的,因此我们进行了一个对称操 作,转动所绕之轴是对称元素之一例,对称元素和对称操作 F 是相关的但不相同的概念,它们常被混淆,一个对称元素是 (a) (b) 一个几何上存在物(点,线或面),相对于它的变换是进行一 图4.1(a)BF:分子(b)转动120°后的BF 个对称操作. 4.1.2对称元素和对称操作的类型 1)真轴和真转动 90
90 第四章 分子的对称性与群论基础 分子的量子力学处理是困难的;我们常常可以从分子的对称性得到有关分子的能级、波函数和分子性 质的定性知识.如象我们在第六章中要看到的一样,分子的对称性或原子周围环境的对称性严格而精确地 决定了一个原子或分子可能具有的能级数目和类型.因此,只要单独从对称性考虑,我们总可以说出问题 的定性特征是什么.不需要任何定量的计算我们就知道有多少能态,在它们之间可能发生哪种相互作用和 跃迁.用另一种方式来说,仅从对称性考虑就可以使我们对“什么是可能的和什么是完全不可能的?”这 个问题给出一个完全而严格的回答。然而,只由对称性考虑不能告诉我们这种可能的事情在实际上发生的 可能性有多大,原则上,对称性可以告诉我们体系的两个状态的能量必然不同,但是,只有经过计算或测 量我们才能决定能量的差别有多大,还有,对称性只能告诉我们在分子的电子光谱或振动光谱中某些吸收 谱带可以发生,但是要知道它们在什么部位发生,强度有多大则需要作计算. 所谓分子的对称性,我们将指核保持固定于其平衡位置所形成的骨架对称性.(对于分子量子力学,我 们的起点将是 Born-Oppenheimer 近似,它认为当求解分子的电子波函数时.核是看作固定的,见第七章).应 当注意,一个分子的对称性在不同的电子状态时可能不同,例如 HCN 在其电子基态时是直线形的,但在某 些激发态时是非直线形的,除非另外指明,我们将只考虑电子基态的对称性,本章由三部分内容组成,第 一部分,4.1-4.4 节,是分子的几何对称性和点群,第二部分,4.5-4.7 节,介绍了群的表示理论;第三部分, 4.8-4.10 节,简述了群论在化学键,分子力学,光谱理论方面的应用. 4.1 对称元素和对称操作 为了建立尽可能有用的分子对称性概念,必须制定一些关于对称性的严格数学标准,为此,首先研究 分子可以具有的对称元素的种类,和由这些对称元素所生成的对称操作,下一节将证明,一个分子的全部 对称操作的集合组成一个数学群. 4.1.1 对称元素和对称操作的定义 对于对称操作,我们意指一个物体这样的变换,其最后位置与最初位置是物理上不可分辨的,同时物 体中各对点的距离保持不变.例如,考虑平面三角形分子 BF3 图 4.1(a),为了方便,我们把其中的氟核标上 号.若我们将分子绕通过硼核并垂直于分子平面的轴逆时针 方向转动 120°,新的位置将如图 4.1(b)所示.由于事实上氟 核彼此在物理上是不可分辨的,因此我们进行了一个对称操 作,转动所绕之轴是对称元素之一例.对称元素和对称操作 是相关的但不相同的概念,它们常被混淆,一个对称元素是 —个几何上存在物(点,线或面),相对于它的变换是进行一 个对称操作. 4.1.2 对称元素和对称操作的类型 1)真轴和真转动 (a) (b) 图 4.1 (a) BF3分子(b)转动 120°后的 BF3 B F1 F2 F3 B F1 F3 F2
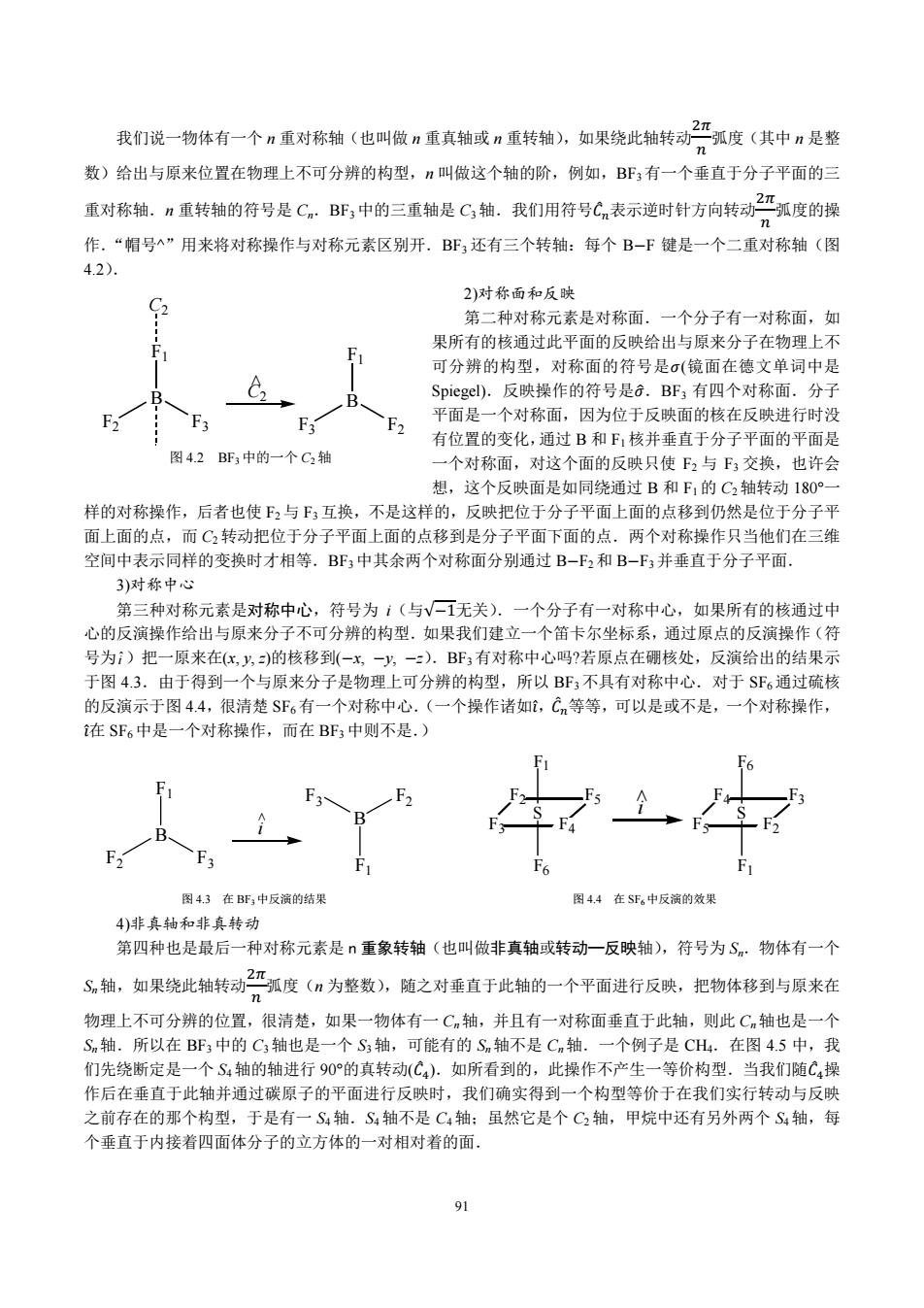
2π 我们说一物体有一个n重对称轴(也叫做n重真轴或n重转轴),如果绕此轴转动一弧度(其中n是整 数)给出与原来位置在物理上不可分辨的构型,n叫做这个轴的阶,例如,BF3有一个垂直于分子平面的三 重对称轴。n重转轴的符号是C.B那,中的三重轴是C,轴。我们用符号C,表示逆时针方向转动严弧度的操 作.“帽号”用来将对称操作与对称元素区别开.BF?还有三个转轴:每个B-F键是一个二重对称轴(图 4.2) 2)对称面和反映 C2 第二种对称元素是对称面.一个分子有一对称面,如 果所有的核通过此平面的反映给出与原来分子在物理上不 可分辨的构型,对称面的符号是σ(镜面在德文单词中是 Spiegel).反映操作的符号是6.BF;有四个对称面.分子 平面是一个对称面,因为位于反映面的核在反映进行时没 有位置的变化,通过B和F:核并垂直于分子平面的平面是 图4.2BF3中的一个C2轴 一个对称面,对这个面的反映只使F2与F3交换,也许会 想,这个反映面是如同绕通过B和F1的C2轴转动180°一 样的对称操作,后者也使F2与F3互换,不是这样的,反映把位于分子平面上面的点移到仍然是位于分子平 面上面的点,而C2转动把位于分子平面上面的点移到是分子平面下面的点.两个对称操作只当他们在三维 空间中表示同样的变换时才相等.BF3中其余两个对称面分别通过B-F2和B-F3并垂直于分子平面. 3)对称中心 第三种对称元素是对称中心,符号为i(与V一1无关).一个分子有一对称中心,如果所有的核通过中 心的反演操作给出与原来分子不可分辨的构型.如果我们建立一个笛卡尔坐标系,通过原点的反演操作(符 号为)把一原来在(x,,)的核移到(-x一y,-).BF3有对称中心吗?若原点在硼核处,反演给出的结果示 于图4.3.由于得到一个与原来分子是物理上可分辨的构型,所以BF3不具有对称中心.对于SF6通过硫核 的反演示于图4.4,很清楚SF6有一个对称中心.(一个操作诸如,Cn等等,可以是或不是,一个对称操作, 在SF6中是一个对称操作,而在BF3中则不是.) F 图4.3在BF3中反演的结果 图4.4在SF6中反演的效果 4)非真轴和非真转动 第四种也是最后一种对称元素是n重象转轴(也叫做非真轴或转动一反映轴),符号为Sm,物体有一个 S,轴,如果绕此轴转动2”弧度(为整数),随之对垂直于此轴的一个平面进行反映,把物体移到与原来在 物理上不可分辨的位置,很清楚,如果一物体有一C,轴,并且有一对称面垂直于此轴,则此Cn轴也是一个 Sn轴.所以在BF3中的C3轴也是一个S3轴,可能有的Sn轴不是Cn轴.一个例子是CH4.在图4.5中,我 们先绕断定是一个S4轴的轴进行90°的真转动(C4).如所看到的,此操作不产生一等价构型.当我们随C4操 作后在垂直于此轴并通过碳原子的平面进行反映时,我们确实得到一个构型等价于在我们实行转动与反映 之前存在的那个构型,于是有一S4轴.S4轴不是C4轴:虽然它是个C2轴,甲烷中还有另外两个S4轴,每 个垂直于内接着四面体分子的立方体的一对相对着的面. 91
91 我们说一物体有一个 n 重对称轴(也叫做 n 重真轴或 n 重转轴),如果绕此轴转动ଶగ 弧度(其中 n 是整 数)给出与原来位置在物理上不可分辨的构型,n 叫做这个轴的阶,例如,BF3 有一个垂直于分子平面的三 重对称轴.n 重转轴的符号是 Cn.BF3 中的三重轴是 C3 轴.我们用符号ܥመ 表示逆时针方向转动ଶగ 弧度的操 作.“帽号^”用来将对称操作与对称元素区别开.BF3 还有三个转轴:每个 BെF 键是一个二重对称轴(图 4.2). 2)对称面和反映 第二种对称元素是对称面.一个分子有一对称面,如 果所有的核通过此平面的反映给出与原来分子在物理上不 可分辨的构型,对称面的符号是ߪ)镜面在德文单词中是 Spiegel).反映操作的符号是ߪො.BF3 有四个对称面.分子 平面是一个对称面,因为位于反映面的核在反映进行时没 有位置的变化,通过 B 和 F1 核并垂直于分子平面的平面是 一个对称面,对这个面的反映只使 F2 与 F3 交换,也许会 想,这个反映面是如同绕通过 B 和 F1的 C2轴转动 180°一 样的对称操作,后者也使 F2 与 F3 互换,不是这样的,反映把位于分子平面上面的点移到仍然是位于分子平 面上面的点,而 C2 转动把位于分子平面上面的点移到是分子平面下面的点.两个对称操作只当他们在三维 空间中表示同样的变换时才相等.BF3 中其余两个对称面分别通过 BെF2 和 BെF3 并垂直于分子平面. 3)对称中心 第三种对称元素是对称中心,符号为 i(与√െ1无关).一个分子有一对称中心,如果所有的核通过中 心的反演操作给出与原来分子不可分辨的构型.如果我们建立一个笛卡尔坐标系,通过原点的反演操作(符 号为i ˆ)把一原来在(x, y, z)的核移到(െx, െy, െz).BF3有对称中心吗?若原点在硼核处,反演给出的结果示 于图 4.3.由于得到一个与原来分子是物理上可分辨的构型,所以 BF3 不具有对称中心.对于 SF6通过硫核 的反演示于图 4.4,很清楚 SF6 有一个对称中心.(一个操作诸如ଓ,̂ ܥመ 等等,可以是或不是,一个对称操作, ଓ在̂ SF6 中是一个对称操作,而在 BF3 中则不是.) B F1 F2 F3 B F1 F3 F2 i < S F6 F1 F3 F2 F4 F5 S F1 F6 F5 F4 F2 F3 i < 图 4.3 在 BF3 中反演的结果 图 4.4 在 SF6 中反演的效果 4)非真轴和非真转动 第四种也是最后一种对称元素是 n 重象转轴(也叫做非真轴或转动—反映轴),符号为 Sn.物体有一个 Sn 轴,如果绕此轴转动ଶగ 弧度(n 为整数),随之对垂直于此轴的一个平面进行反映,把物体移到与原来在 物理上不可分辨的位置,很清楚,如果一物体有一 Cn 轴,并且有一对称面垂直于此轴,则此 Cn轴也是一个 Sn 轴.所以在 BF3 中的 C3 轴也是一个 S3 轴,可能有的 Sn轴不是 Cn轴.一个例子是 CH4.在图 4.5 中,我 们先绕断定是一个 S4 轴的轴进行 90°的真转动(ܥመ ସ).如所看到的,此操作不产生一等价构型.当我们随ܥመ ସ操 作后在垂直于此轴并通过碳原子的平面进行反映时,我们确实得到一个构型等价于在我们实行转动与反映 之前存在的那个构型,于是有一 S4轴.S4 轴不是 C4 轴;虽然它是个 C2轴,甲烷中还有另外两个 S4轴,每 个垂直于内接着四面体分子的立方体的一对相对着的面. 图 4.2 BF3中的一个 C2 轴 B F1 F2 F3 C2 B F1 F3 F2 C2 <
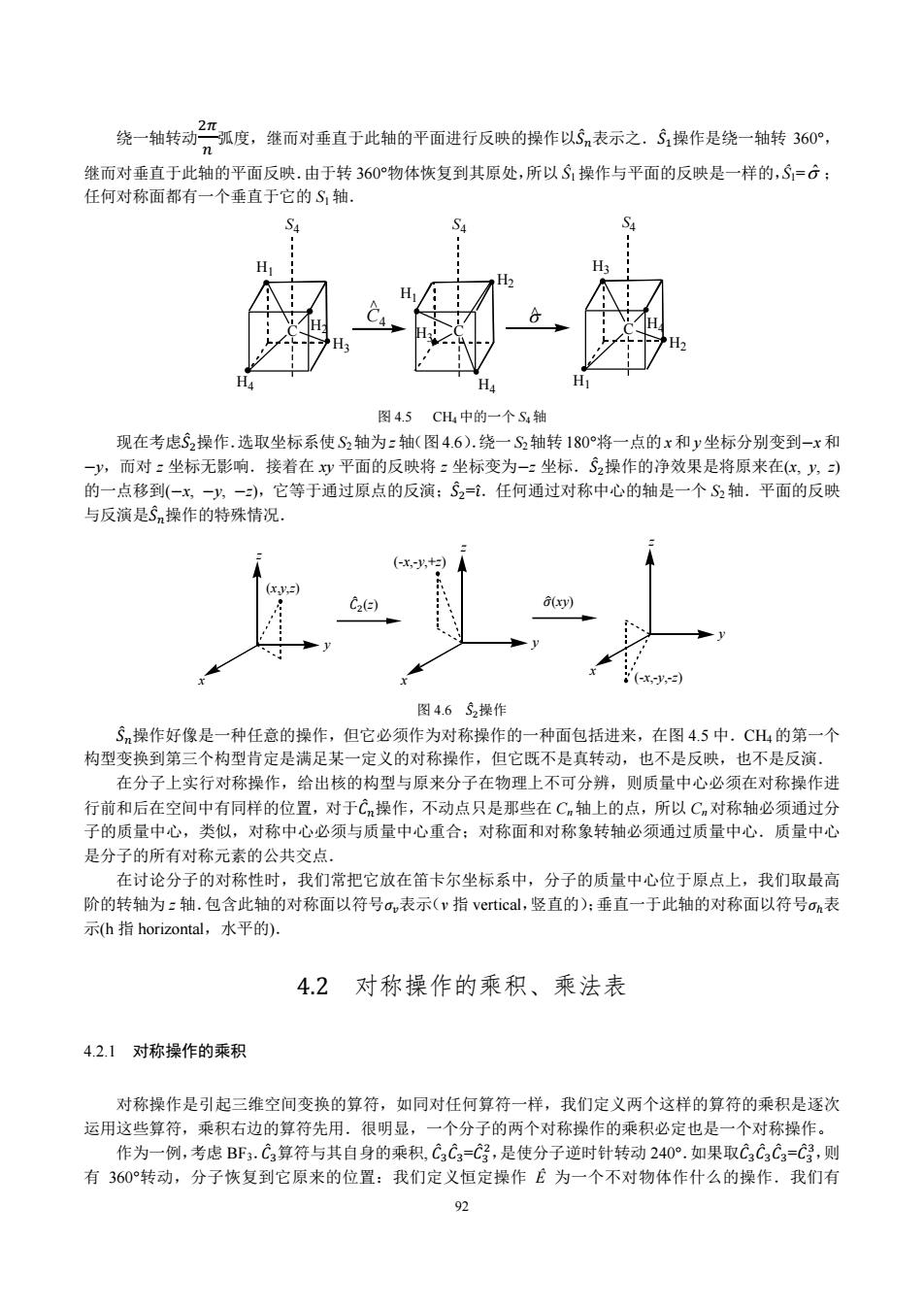
绕一轴转动 严弧度,继而对垂直于此轴的平面进行反映的操作以S,表示之.$操作是绕一轴转360°, 继而对垂直于此轴的平面反映.由于转360°物体恢复到其原处,所以S操作与平面的反映是一样的,S=G: 任何对称面都有一个垂直于它的S,轴. H: 2 H 图4.5CH中的一个S4轴 现在考虑S2操作.选取坐标系使S2轴为z轴(图4.6).绕一S2轴转180°将一点的x和y坐标分别变到-x和 -y,而对:坐标无影响.接着在y平面的反映将:坐标变为-二坐标.S2操作的净效果是将原来在(化,y,) 的一点移到(-x,-y,一-),它等于通过原点的反演:S2=1.任何通过对称中心的轴是一个S2轴。平面的反映 与反演是Sn操作的特殊情况. (-x,y,+) (xy,2】 C2() (y) 0(-x,y,-) 图4.652操作 Sm操作好像是一种任意的操作,但它必须作为对称操作的一种面包括进来,在图4.5中.CH4的第一个 构型变换到第三个构型肯定是满足某一定义的对称操作,但它既不是真转动,也不是反映,也不是反演. 在分子上实行对称操作,给出核的构型与原来分子在物理上不可分辨,则质量中心必须在对称操作进 行前和后在空间中有同样的位置,对于Cn操作,不动点只是那些在Cn轴上的点,所以Cm对称轴必须通过分 子的质量中心,类似,对称中心必须与质量中心重合:对称面和对称象转轴必须通过质量中心.质量中心 是分子的所有对称元素的公共交点. 在讨论分子的对称性时,我们常把它放在笛卡尔坐标系中,分子的质量中心位于原点上,我们取最高 阶的转轴为:轴.包含此轴的对称面以符号ov表示(v指vertical,竖直的):垂直一于此轴的对称面以符号oh表 示(h指horizontal,.水平的), 4.2对称操作的乘积、乘法表 4.2.1对称操作的乘积 对称操作是引起三维空间变换的算符,如同对任何算符一样,我们定义两个这样的算符的乘积是逐次 运用这些算符,乘积右边的算符先用.很明显,一个分子的两个对称操作的乘积必定也是一个对称操作。 作为一例,考虑BF3.C3算符与其自身的乘积,C3C3=C好,是使分子逆时针转动240°.如果取C3C3C3=C,则 有360°转动,分子恢复到它原来的位置:我们定义恒定操作E为一个不对物体作什么的操作,我们有 8
92 绕一轴转动ଶగ 弧度,继而对垂直于此轴的平面进行反映的操作以ܵመ 表示之.ܵመ ଵ操作是绕一轴转 360°, 继而对垂直于此轴的平面反映.由于转 360°物体恢复到其原处,所以 Ŝ1 操作与平面的反映是一样的,Ŝ1=ˆ ; 任何对称面都有一个垂直于它的 S1轴. C H1 H2 H3 H4 S4 C H3 H4 H2 H1 S4 C H1 H2 H3 H4 S4 C4 < < 图 4.5 CH4中的一个 S4轴 现在考虑ܵመ ଶ操作.选取坐标系使 S2轴为 z 轴(图 4.6).绕一 S2轴转 180°将一点的 x 和 y 坐标分别变到െx 和 െy,而对 z 坐标无影响.接着在 xy 平面的反映将 z 坐标变为െz 坐标.ܵመ ଶ操作的净效果是将原来在(x, y, z) 的一点移到(െx, െy, െz),它等于通过原点的反演;ܵመ ଶ=ଓ.任何通过对称中心的轴是一个 ̂ S2 轴.平面的反映 与反演是ܵመ 操作的特殊情况. x y z (x,y,z) x y z (-x,-y,+z) x y z (-x,-y,-z) 图 4.6 ܵመ ଶ操作 ܵመ 操作好像是一种任意的操作,但它必须作为对称操作的一种面包括进来,在图 4.5 中.CH4 的第一个 构型变换到第三个构型肯定是满足某一定义的对称操作,但它既不是真转动,也不是反映,也不是反演. 在分子上实行对称操作,给出核的构型与原来分子在物理上不可分辨,则质量中心必须在对称操作进 行前和后在空间中有同样的位置,对于ܥመ 操作,不动点只是那些在 Cn 轴上的点,所以 Cn对称轴必须通过分 子的质量中心,类似,对称中心必须与质量中心重合;对称面和对称象转轴必须通过质量中心.质量中心 是分子的所有对称元素的公共交点. 在讨论分子的对称性时,我们常把它放在笛卡尔坐标系中,分子的质量中心位于原点上,我们取最高 阶的转轴为 z 轴.包含此轴的对称面以符号ߪ௩表示(v 指 vertical,竖直的);垂直一于此轴的对称面以符号ߪ表 示(h 指 horizontal,水平的). 4.2 对称操作的乘积、乘法表 4.2.1 对称操作的乘积 对称操作是引起三维空间变换的算符,如同对任何算符一样,我们定义两个这样的算符的乘积是逐次 运用这些算符,乘积右边的算符先用.很明显,一个分子的两个对称操作的乘积必定也是一个对称操作。 作为一例,考虑 BF3.ܥመ ଷ算符与其自身的乘积, ܥመ ଷܥመ ଷ=ܥመ ଷ ଶ,是使分子逆时针转动 240°.如果取ܥመ ଷܥመ ଷܥመ ଷ=ܥመ ଷ ଷ,则 有 360°转动,分子恢复到它原来的位置:我们定义恒定操作 Ê 为一个不对物体作什么的操作.我们有 መܥ ଶ(z) ߪො(xy)

C=E.(符号来自德文单词Einheit,意为l.有些书用符号i,代替E). 现在考虑一个有六重对称轴的分子,例如,C6H6.C6操作是转动60°,C名是转动120°,于是C名=C。并 且C经=C2。我们断定C6对称轴也是C2轴和C3轴,一般地说,一个Cn轴也是一个Cm轴,如果m是整数 的话. 由于对一个平面的两个相继的反映将所有的核移回原位,所以有2=E.并且2=E.更一般地说,对于 偶数n,6n=E,=E,而对于奇数n,6n=6,=i. 对称操作算符总是可以对易的吗?考虑SF6。我们来检验绕:轴的C4转动和绕x轴的C2转动的乘积,图 4.7指出,C4(e)C2(x)≠C2(x)C4(日).所以对称操作不总是可以对易的.[注意:我们对于一个固定的坐标系来 描述对称操作:我们的规定是,当我们实行一对称操作时,对称元素不随分子而动,而是在空间保持固定.例 如,当我们实行C4(e)操作时,C2(x)轴不动.] x) 图4.7(a)C2(x)C4(a)(b)C4(e)C2(x) 4.2.2对称元素和对称操作之间的一般关系 这里我们介绍关于不同种类的对称元素和操作如何相互关联的一些有用的规则,处理方法是,某两个 对称元素的存在要求其它元素存在,以及对称操作间的交换关系.这些叙述不给证明:做出努力去证明它 们对读者是有裨益的。 乘积关系 (1)两个真转动的乘积必定是一个真转动.因此,虽然转动可由一些平面的联合反映所产生(见规则2), 但是,反过来却是不可能的. (2)在相交成中B角的平面A和B内的两个反映,其乘积是绕交线所定义的轴的2中4B转动.最简单的证 明是几何方法,如图4.8所示,显然,这一规则具有某种深刻的推论,若两个平面分开成中4B角,则要求存 在一个Cn轴,n=2π/2中8.这里n必须是一个整数,而且Cn轴将保证总共存在n个这样的平面.因此两个 平面意味着构成Cm群(参看下文)的操作的完整集合存在, (3)若存在一个转动轴Cn和一个包含它的平面,则必存在n个被 分开成2π2n角的平面.这是从规则2得出的推论. B (4)绕相交成0角的轴的两个C2转动的乘积,是一个绕垂直于C2 轴平面的另一轴的20转动.这可以用类似于图4.8的图解方式从几 何上予以证明,它还意味着一个Cn轴和一个垂直的C2轴,要求存在 一组n个C2轴,并由此生成我们即将见到的Dn群。 (⑤)一个偶数阶的真转动轴和一个垂直的反映面生成一个反演中 心,即Cn=Cn=C2=C2=i.类似地,Cni=iCn=C2i=iC2=6 交换关系 下列对称操作永远是可交换的: 图4.8几何证明两个反映面A和B要 ①两个绕同一个轴的转动. ③通过相互垂直的平面的反映, 求沿它们的交线存在一个Cn轴, ③反演和任一反映或转动. n=2π/2pB,中4B=a+B,x=2(a+B), .=2中4B 93
93 መܥ ଷ ଷ=ܧ).符号来自德文单词 Einheit,意为 1.有些书用符号ܫ መ,代替ܧ.( 现在考虑一个有六重对称轴的分子,例如,C6H6.ܥመ 操作是转动 60°,ܥመ ଶ是转动 120°,于是ܥመ ଶ=ܥመ ଷ ଵ。并 且ܥመ ଷ=ܥመ ଶ ଵ。我们断定 C6 对称轴也是 C2 轴和 C3 轴,一般地说,一个 Cn 轴也是一个 Cm轴,如果 n/m 是整数 的话. 由于对一个平面的两个相继的反映将所有的核移回原位,所以有ߪොଶ=ܧ.并且ଓ̂ ଶ=ܧ.更一般地说,对于 偶数 n,ߪො=ܧ,ଓ̂ =ܧ,而对于奇数 n,ߪො=ߪො,ଓ̂ =ଓ.̂ 对称操作算符总是可以对易的吗?考虑 SF6。我们来检验绕 z 轴的ܥመ ସ转动和绕 x 轴的ܥመ ଶ转动的乘积,图 4.7 指出,ܥመ ସ(z)ܥመ ଶ(x)≠ܥመ ଶ(x)ܥመ ସ(z).所以对称操作不总是可以对易的.[注意:我们对于一个固定的坐标系来 描述对称操作;我们的规定是,当我们实行一对称操作时,对称元素不随分子而动,而是在空间保持固定.例 如,当我们实行ܥመ ସ(z)操作时,ܥመ ଶ(x)轴不动.] S F6 F1 F3 F2 F4 F5 C4(z) < z x y S F6 F1 F2 F5 F3 F4 z x y S F1 F6 F3 F4 F2 F5 z x y C2(x) < S F6 F1 F3 F2 F4 F5 C2(x) < z x y S F1 F6 F4 F5 F3 F2 z x y S F1 F6 F5 F2 F4 F3 z x y C4(z) < (a) (b) 图 4.7 (a)ܥመ ଶ(x)ܥመ ସ(z) (b)ܥመ ସ(z)ܥመ ଶ(x) 4.2.2 对称元素和对称操作之间的一般关系 这里我们介绍关于不同种类的对称元素和操作如何相互关联的一些有用的规则,处理方法是,某两个 对称元素的存在要求其它元素存在,以及对称操作间的交换关系.这些叙述不给证明;做出努力去证明它 们对读者是有裨益的. 乘积关系 (1)两个真转动的乘积必定是一个真转动.因此,虽然转动可由一些平面的联合反映所产生(见规则 2), 但是,反过来却是不可能的. (2)在相交成 ϕAB角的平面 A 和 B 内的两个反映,其乘积是绕交线所定义的轴的 2ϕAB转动.最简单的证 明是几何方法,如图 4.8 所示,显然,这一规则具有某种深刻的推论,若两个平面分开成 ϕAB 角,则要求存 在一个 Cn 轴,n=2ߨ/2ϕAB.这里 n 必须是一个整数,而且 Cn 轴将保证总共存在 n 个这样的平面.因此两个 平面意味着构成 Cnv群(参看下文)的操作的完整集合存在. (3)若存在一个转动轴 Cn和一个包含它的平面,则必存在 n 个被 分开成 2ߨ/2n 角的平面.这是从规则 2 得出的推论. (4)绕相交成 θ 角的轴的两个ܥመ ଶ转动的乘积,是一个绕垂直于 C2 轴平面的另一轴的 2θ 转动.这可以用类似于图 4.8 的图解方式从几 何上予以证明,它还意味着一个 Cn轴和一个垂直的 C2 轴,要求存在 一组 n 个 C2轴,并由此生成我们即将见到的 Dn 群。 (5)一个偶数阶的真转动轴和一个垂直的反映面生成一个反演中 心,即ܥመ ଶ መܥොߪ=ොߪ ଶ መܥ= ଶߪො=ߪොܥመ ଶ=ଓ.类似地, ̂ ܥመ ଶ ଓ= ̂ ଓܥ̂መ ଶ መܥ= ଶଓ=̂ ଓܥ̂መ ଶ=ߪො. 交换关系 下列对称操作永远是可交换的: ①两个绕同一个轴的转动. ③通过相互垂直的平面的反映, ③反演和任一反映或转动. B β x β α A α 图 4.8 几何证明两个反映面 A 和 B 要 求沿它们的交线存在一个 Cn 轴, n=2ߨ/2ϕAB,ϕAB= ߙ ߚ,x=2(ߙߚ,( ∴x=2ϕAB