6.2 Hartree六程 变0 自洽场计算(SCF) R-eq+营p J。=p上中0t,dt Solution:Self-Consistent Field (SCF) 2会22e0r片p@eo@ i p(r)=Φ(ri-th电子的密度分布 2 pm回=立p回=立,2 总电子密度 No Converged? yes >11 Stop
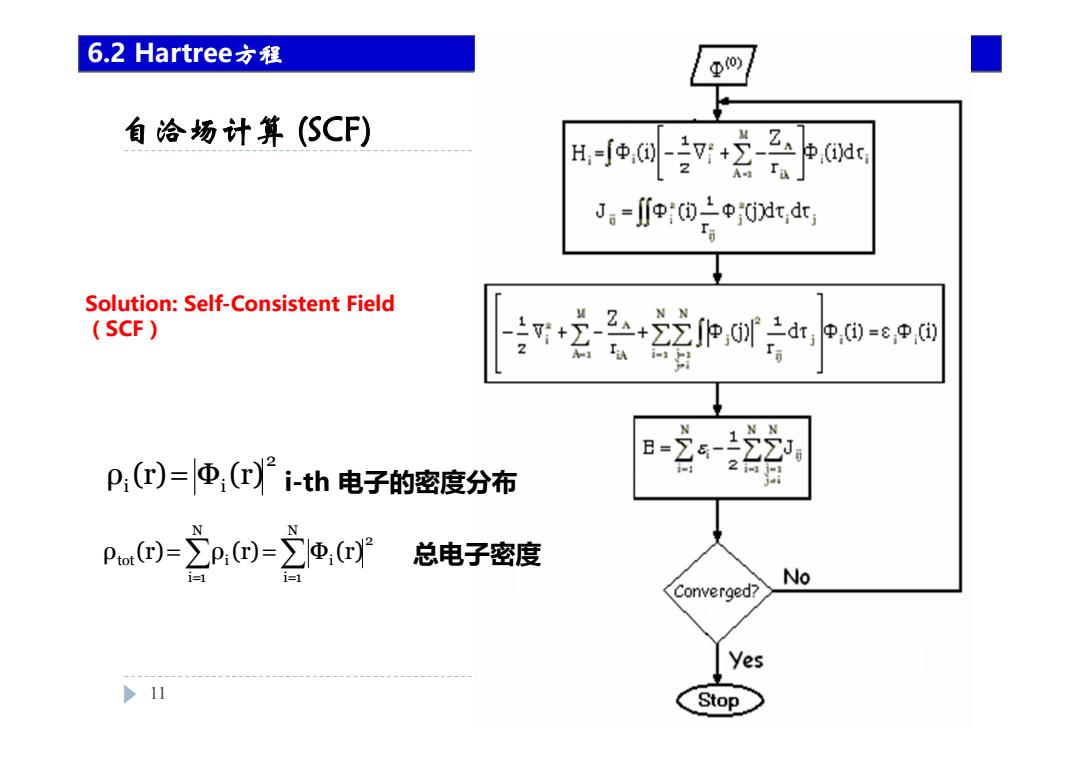
自洽场计算 (SCF) 11 Chapter 6 HF 6.2 Hartree方程 Solution: Self-Consistent Field (SCF) 2 i i ρ (r)= Φ (r) i-th 电子的密度分布 = = = = N i 1 2 i N i 1 tot i ρ (r) ρ (r) Φ (r) 总电子密度

6.3 Hartree-Fock方程 N电子体条的Slater波函数 HP波函数 不满足电子(费米子)全同性要求的波函数反对成性 如:双粒子体系 PROBLEM =p(1)9,(2)是两电子体系本征方程的解 (a) 交换算符P12户2[p,(1)9(2)]=p(2)m()≠-p(1)9,(2) 也是本征解 ·(b 则满足交换反对称条件的波函数: Slater行列式形式(SD) For fermions the negative ”=方[0%(2)-g.2)m]一 1 p.(1) P(1) sign must be used,so that goes t 9,(2) a and b are identical. √2p(2) p1(1) P2(1) pw(1) Fock,Slater 1930( 91(2) p2(2) px(2) =p1,p…pw》 (N) 2(N) (N) 满足反对称条件:改变行列式的两列元素(两个粒子互换坐标),行列式 符号改变 满足Pau不相容原理:两个或连个以上粒子相同的时候,SD=0 >12 Chapter 6 HF
N电子体系的Slater波函数 12 Chapter 6 HF 6.3 Hartree-Fock方程 满足反对称条件:改变行列式的两列元素(两个粒子互换坐标),行列式 符号改变 满足Pauli不相容原理: 两个或连个以上粒子相同的时候,SD=0 HP 波函数 Fock, Slater 1930

6.3 Hartree-Fock六程 Hartree-Fock方程 Fock,Slater 1930 Φx1) Φ2X1) ΦN(x1) 平。=平H=平sD(,5,N)=(Ny)Ve|,(2) Φ2(X2) Φ(X2) ΦXN) 2XN)…ΦxN) E=w-立H+220,-K, 电子相互作用项 2i-1j- Svonv odrde-Ju- H-fo(bo.()dr-f(-iV:+vw.(dr 12 J=j小Φ2)drd 电子间的库仑排斥能 K=∬®cc',c地cdd 同自旋电子的交换能 Slater行列式比HP波函数多出的部分 >13 Chapter 6 HF
Hartree-Fock方程 13 Chapter 6 HF 6.3 Hartree-Fock方程 Fock, Slater 1930 电子间的库仑排斥能 同自旋电子的交换能 Slater行列式比HP波函数多出的部分 = = = = = + − N i 1 N j 1 ij ij N i 1 i SD SD (J K ) 2 1 E Ψ HΨ H = = − ∇ + v Φ (r)dr 21 H Φ (r)hΦ (r)dr Φ (r) i i 2i * i i i * i i i 2 j 2 1 2 1 2 1 * 1 j * ij i Φ (r )Φ (r )drdr r r 1 K Φ (r )Φ (r ) − = = 1 2 2j 12 2 ij i Φ (2)drdr r1 J Φ (1) 电子相互作用项 Φ (x ) Φ (x ) ... Φ (x ) Φ (x ) Φ (x ) ... Φ (x ) Φ (x ) Φ (x ) ... Φ (x ) Ψ Ψ Ψ (r ,r ,...,r ) (N!) 1 N 2 N N N 1 2 2 2 N 2 1 1 2 1 N 1 1/2 1 2 N SD 0 HF − ≈ = =

6.3 Hartree-Fock方程 Hartree-Fock方程 exchange operator: xo0-0ow.po Minimizing the energy by varying the spin orbitals leads to the Hartree-Fock equations: [+v*2o,fot,efd,=e@国 Fock operator: f=h+∑,-K)→ molecular orbital energies: e=Φ地)=H+J-K) >14 Chapter 6 HF
Hartree-Fock方程 14 Chapter 6 HF 6.3 Hartree-Fock方程 Φ (2)dτ Φ (1) r 1 K (1)Φ (1) Φ (2) i 2 j 12 j i j = exchange operator: = = + − = Φ − ∇ + Nj 1 i j j i *j Nj 1 i j 2 i i j 2i Φ (r)dτ (r) r - r' 1 Φ (r)dτ Φ (r')Φ (r') r - r' 1 v Φ (r) Φ (r') 21 i ε Minimizing the energy by varying the spin orbitals leads to the Hartree-Fock equations: = = + − N j 1 i i j j f h (J K ) Fock operator: = = = + − N j 1 i i i i i ij ij ε Φ f Φ H (J K ) molecular orbital energies:

6.4 Hartree-Fock-Roothaan方程 LCAO-MO Roothann Linear Combination of Atomic Orbital-Molecular Orbital (LCAO-MO) K ,=2cnP i=1,2,K {p,}-a set of known functions:原子基or平面波基 =1 基组的选择决定了波函数的准确性 f(G)∑cmp(G)=e∑cP(G) matrix equation for the c coefficients Multiplying by()on the left and integrating we get: ∑cn∫pa()f()p,()d1=6,∑c∫pa()pv()d Fw=∫pa)fp,G)dt Fock matrix(KxK Hermitian matrix) S=()o()dr -overlap matrix(KxK Hermitian matrix) ∑Fmw=e,∑Smcu, i=1,2,,K -Roothaan equations >15 Chapter 6 HF
LCAO-MO 15 Chapter 6 HF 6.4 Hartree-Fock-Roothaan方程 Roothann Linear Combination of Atomic Orbital – Molecular Orbital (LCAO-MO) = Φ = K i i c μ 1 μϕ μ i=1,2,...,K {ϕμ} – a set of known functions : 原子基 or 平面波基 基组的选择决定了波函数的准确性