
22液压与气压传动第4版 微小圆柱体作为研究对象。设其半径为「, d 长度为1,作用在两端面的压力分别为P1和 P2,作用在侧面的内摩擦力为F。液流在 做匀速运动时受力平衡,故有 (P1P2)rr2=F 由式(1-4)知内摩擦力F,= -2πrμdu/dr(因流速u随r的增大而减小, 故du/dr为负值,所以加一负号)。令△p= 图1-17圆管层流运动 P1-P2,并将F代入上式整理可得 du=- p rdr μ 对上式积分,并应用边界条件,当r=R时,u=0,得 0 (1-33) 可见管内液体质点的流速在半径方向上按抛物线规律分布。最小流速在管壁r=R处,“m。=0; 最大流速发生在轴线r=0处,“mx=△pR2/4ul。 2.通过管道的流量 .2(R2-2) 对于微小环形通流截面面积dA=2mrd,所通过的流量dq=udA=2murd=2m rdr,于是积分得 9= 2 (R2-2)d=R 4μl 128u4p (1-34) 3.管道内的平均流速 根据平均流速的定义,可得 91R4R2 d2 V= ATR28μl P=8uAp=32Ap AP= (1-35) 将式(1-35)与um,值比较可知,平均流速v为最大流速的1/2。 4.沿程压力损失 从式(1-35)中求出△p即为沿程压力损失 32μlu △p=4p= (1-36) d2 由式(1-36)可知,液流在直管中做层流流动时,其沿程压力损失与管长、流速、黏度成正 比,而与管径的平方成反比。适当变换式(1-36),可写成如下形式 64 1 pu2 I pv2 APx=Red 2=A d 2 (1-37) 式中入一沿程阻力系数,理论值入=64/R。考虑实际流动中的油温变化不匀等问题,因而 在实际计算时,对金属管取入=75/Re,橡胶软管取A=80/Re。 在液压传动中,因为液体自重和位置变化对压力的影响很小而可以忽略,所以在水平管 的条件下推导的公式(1-37)同样适用于非水平管。 (二)湍流时的沿程压力损失 液体在等直径圆管中做湍流流动时的沿程压力损失要比层流时大得多,因为它不仅要克 服液层间的内摩擦,还要克服由于液体横向脉动而引起的湍流摩擦,且后者远大于前者。实 验证明,湍流时的沿程压力损失计算可采用层流时的计算公式,但式中的沿程阻力系数入除
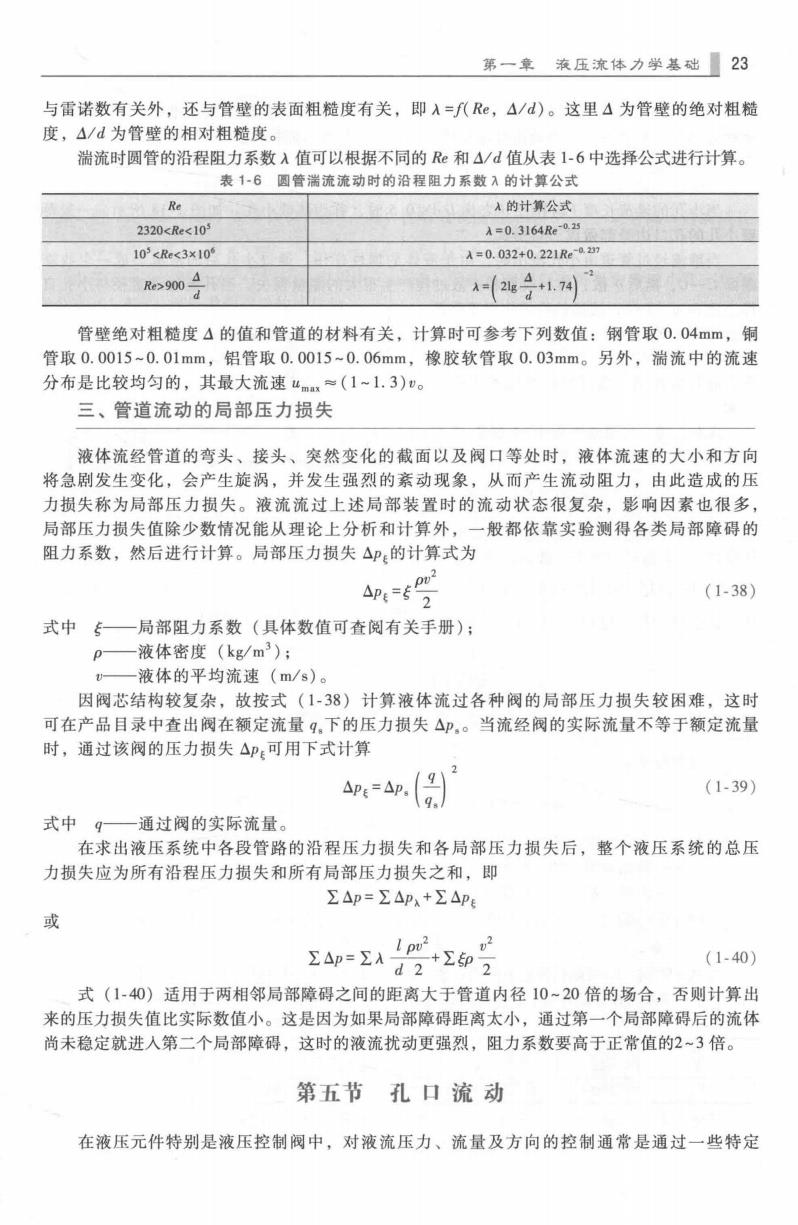
第一章液压流体力学基础23 与雷诺数有关外,还与管壁的表面粗糙度有关,即入=f(Re,△/d)。这里△为管壁的绝对粗糙 度,△/d为管壁的相对粗糙度。 湍流时圆管的沿程阻力系数入值可以根据不同的R和△/d值从表1-6中选择公式进行计算。 表1-6圆管满流流动时的沿程阻力系数入的计算公式 Re 入的计算公式 2320<Re<10 A=0.3164Re-0.25 103<Re<3×10 A=0.032+0.221Re027 Re>9004 d A(2s子1.7网 管壁绝对粗糙度4的值和管道的材料有关,计算时可参考下列数值:钢管取0.04mm,铜 管取0.0015~0.01mm,铝管取0.0015~0.06mm, 橡胶软管取0.03mm。另外,湍流中的流速 分布是比较均匀的,其最大流速“mx≈(1~1.3)v。 三、管道流动的局部压力损失 液体流经管道的弯头、接头、突然变化的截面以及阀口等处时,液体流速的大小和方向 将急剧发生变化,会产生旋涡,并发生强烈的紊动现象,从而产生流动阻力,由此造成的压 力损失称为局部压力损失。液流流过上述局部装置时的流动状态很复杂,影响因素也很多, 局部压力损失值除少数情况能从理论上分析和计算外,一般都依靠实验测得各类局部障碍的 阻力系数,然后进行计算。局部压力损失△P:的计算式为 2 △P:=52 (1-38) 式中一局部阻力系数(具体数值可查阅有关手册); p—液体密度(kg/m3): —液体的平均流速(m/s)。 因阀芯结构较复杂,故按式(1-38)计算液体流过各种阀的局部压力损失较困难,这时 可在产品目录中查出阀在额定流量q。下的压力损失△。当流经阀的实际流量不等于额定流量 时,通过该阀的压力损失△P:可用下式计算 p:=△p (1-39) 式中q一通过阀的实际流量。 在求出液压系统中各段管路的沿程压力损失和各局部压力损失后,整个液压系统的总压 力损失应为所有沿程压力损失和所有局部压力损失之和,即 ∑△p=∑△p,+∑△pE 或 lpmw2.2 Σ4p=ΣAd2+Σ卸2 (1-40) 式(1-40)适用于两相邻局部障碍之间的距离大于管道内径10~20倍的场合,否则计算出 来的压力损失值比实际数值小。这是因为如果局部障碍距离太小,通过第一个局部障碍后的流体 尚未稳定就进人第二个局部障碍,这时的液流扰动更强烈,阻力系数要高于正常值的2~3倍。 第五节孔口流动 在液压元件特别是液压控制阀中,对液流压力、流量及方向的控制通常是通过一些特定

24液压与气压传动第4版 的孔口实现的,它们对流过的液体形成阻力,使其产生压降,其作用类似电路中的电阻,因 此称为液阻。本节主要介绍液流经过孔口的流量公式及液阻的特性。 一、薄壁小孔 当小孔的通流长度1与孔径d之比l/d≤0.5时,称为薄壁小孔。如图1-18所示,一般薄 壁小孔的孔口边缘都做成刃口形式。 当液流经过管道由小孔流出时,由于液体的惯性作用,通过小孔后的液流形成一个收缩 断面C一C,然后扩散,这一收缩和扩散过程产生很大的能量损失。当孔前通道直径与小孔直 径之比D/d≥7时,液流的收缩作用不受孔 前通道内壁的影响,这时的收缩称为完全 收缩;当D/d<7时,孔前通道对液流进人 小孔起导向作用,这时的收缩称为不完全 收缩。 现对孔前、后通道断面1一1和2一2列 伯努利方程,并设动能修正系数α=1,则有 p1近_P2,吃 +∑hE (1-41) pg 2g pg 2g 图1-18通过薄壁小孔的液流 式(1-41)中的∑h:为液流流经小孔的局部 (扫描二维码获得原理动画) 能量损失,它包括两部分:液流经截面突然 缩小时的h:和突然扩大时的h2。h1=知/(2g),经查手册,h2=(1-A/A2)/(2g)。因为A.<42, 所以∑h:=hg+h2=(传+1)m/(2g)。又因为A1=A2时,,=2,将这些关系代入伯努利方程,得出 1 (p1-P2)=C, 2△p U。= (1-42) VE+IV P p 式(1-42)中的C,= 称为速度系数,它反映了局部阻力对速度的影响。 E+I 经过薄壁小孔的流量为 q=Ae。=C.Ao"。=C。C,Ao, 2AP =CaAo 2△p (1-43) p 式中A。一小孔截面积; C。—截面收缩系数,C。=Ae/Ao; Ca一流量系数,Ca=C,C。 流量系数C的大小一般由实验确定,在液流完全收缩的情况下,Re≤I0时,C:可由下式计算 Ca=0.964Re-0.o5 (1-44) 当R>10时,C:可以认为是不变的常数,计算时按Ca=0.60~0.61选取。液流不完全收缩时, C可按表1-7来选择。这时由于管壁对液流进入小孔起导向作用,C可增大至0.7~0.8。 表1-7不完全收缩时流量系数C:的值 0.1 0.2 0.3 0.4 0.5 0.6 0.7 A Ca 0.602、 0.615 0.634 0.661 0.696 0.742 0.804 薄壁小孔因其沿程阻力损失非常小,通过小孔的流量与油液黏度无关,即对油温的变化 不敏感,因此薄壁小孔多用作调节流量的节流器
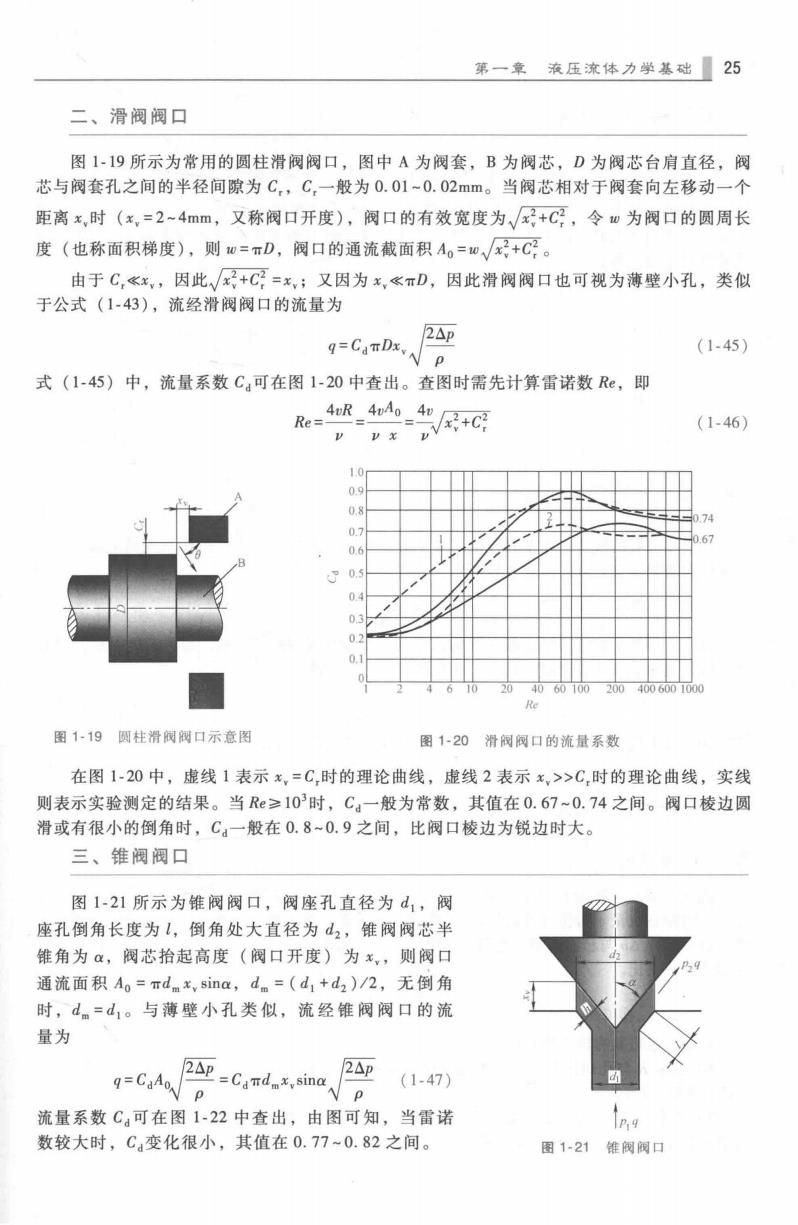
第一章液压流体力学基础【25 二、滑阀阀口 图1-19所示为常用的圆柱滑阀阀口,图中A为阀套,B为阀芯,D为阀芯台肩直径,阀 芯与阀套孔之间的半径间隙为C,C,一般为0.01~0.02mm。当阀芯相对于阀套向左移动一个 距离x,时(x,=2~4mm,又称阀口开度),阀口的有效宽度为,√+C,令w为阀口的圆周长 度(也称面积梯度),则0=πD,阀口的通流截面积A。=0,√+C。 由于C,《。,因此√+C=x,;又因为x,<πD,因此滑阀阀口也可视为薄壁小孔,类似 于公式(1-43),流经滑阀阀口的流量为 q=CaTDxy 2△p (1-45) 式(1-45)中,流量系数C:可在图1-20中查出。查图时需先计算雷诺数Re,即 Re=4R-4A。_4知 x+C2 (1-46) 0.9 74 0 2040601002004006001000 Re 图1-19圆柱滑阀阀口示意图 图1-20滑阀阀口的流量系数 在图1-20中,虚线1表示x,=C,时的理论曲线,虚线2表示x,>>C,时的理论曲线,实线 则表示实验测定的结果。当R≥103时,C:一般为常数,其值在0.67~0.74之间。阀口棱边圆 滑或有很小的倒角时,C:一般在0.8~0.9之间,比阀口棱边为锐边时大。 三、锥阀阀口 图1-21所示为锥阀阀口,阀座孔直径为d1,阀 座孔倒角长度为1,倒角处大直径为d2,锥阀阀芯半 锥角为α,阀芯拾起高度(阀口开度)为x,则阀口 通流面积Ao=rdmx,sina,dm=(d1+d2)/2,无倒角 时,d。=d1。与薄壁小孔类似,流经锥阀阀口的流 量为 2p=,sina、 2Ap (1-47) 流量系数C:可在图1-22中查出,由图可知,当雷诺 P9 数较大时,C:变化很小,其值在0.77~0.82之间。 图1-21锥阀阀口
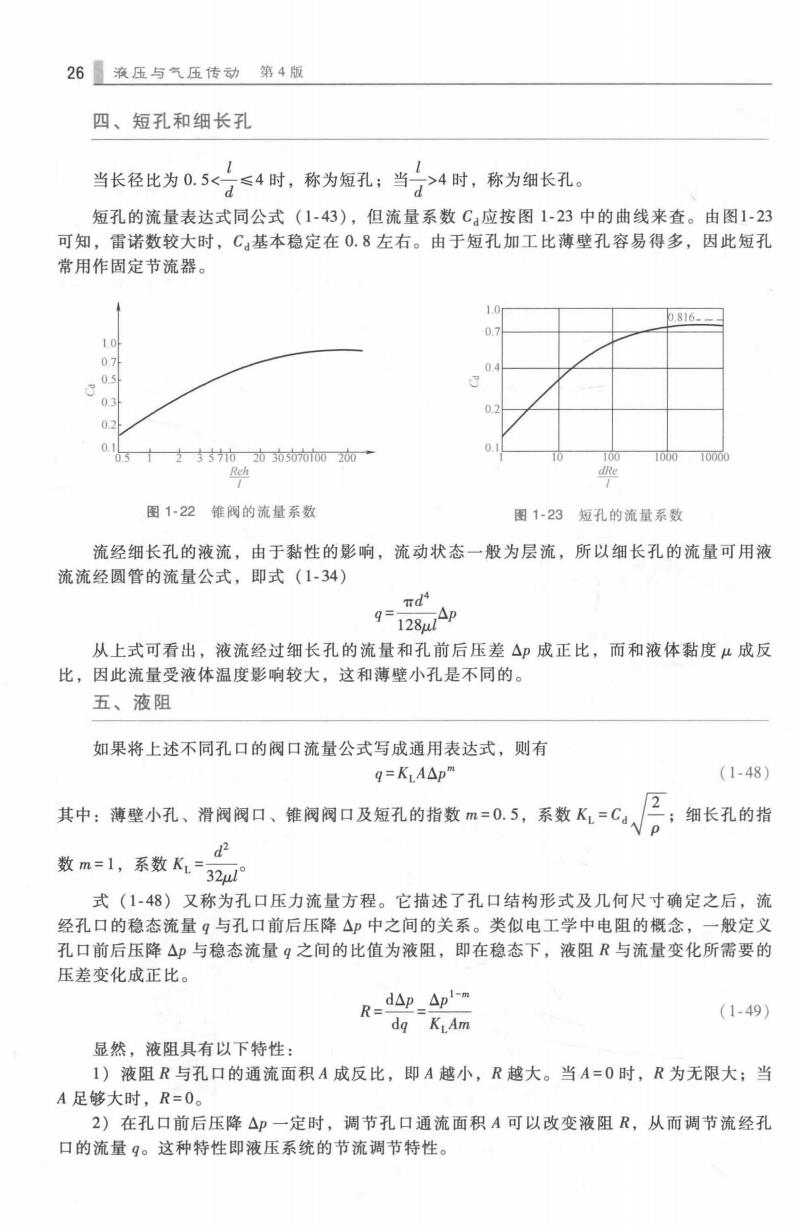
26液压与气压传动第4版 四、短孔和细长孔 当长径比为0,5<≤4时,称为短孔:当子>4时,称为细长孔。 短孔的流量表达式同公式(1-43),但流量系数C:应按图1-23中的曲线来查。由图1-23 可知,雷诺数较大时,C基本稳定在0.8左右。由于短孔加工比薄壁孔容易得多,因此短孔 常用作固定节流器。 1.0 0816. 0.7 10 0.7 04 as/ 03 0.2 02 0.1 5十2357003t5000020一 0. 100 100010000 Reh dRe 图1-22锥阀的流量系数 图1-23短孔的流量系数 流经细长孔的液流,由于黏性的影响,流动状态一般为层流,所以细长孔的流量可用液 流流经圆管的流量公式,即式(1-34) ndi 9128uA 从上式可看出,液流经过细长孔的流量和孔前后压差△p成正比,而和液体黏度4成反 比,因此流量受液体温度影响较大,这和薄壁小孔是不同的。 五、液阻 如果将上述不同孔口的阀口流量公式写成通用表达式,则有 q=KA△pm (1-48) 2 其中:薄壁小孔、滑阀阀口、锥阀阀口及短孔的指数m=0.5,系数KL=Ca√ ;细长孔的指 2 数m=1,系数K1-32 式(1-48)又称为孔口压力流量方程。它描述了孔口结构形式及几何尺寸确定之后,流 经孔口的稳态流量g与孔口前后压降△中之间的关系。类似电工学中电阻的概念,一般定义 孔口前后压降△p与稳态流量g之间的比值为液阻,即在稳态下,液阻R与流量变化所需要的 压差变化成正比。 R=d4p、4pl-m (1-49) dg KLAm 显然,液阻具有以下特性: 1)液阻R与孔口的通流面积A成反比,即A越小,R越大。当A=0时,R为无限大;当 A足够大时,R=0。 2)在孔口前后压降△p一定时,调节孔口通流面积A可以改变液阻R,从而调节流经孔 口的流量q。这种特性即液压系统的节流调节特性