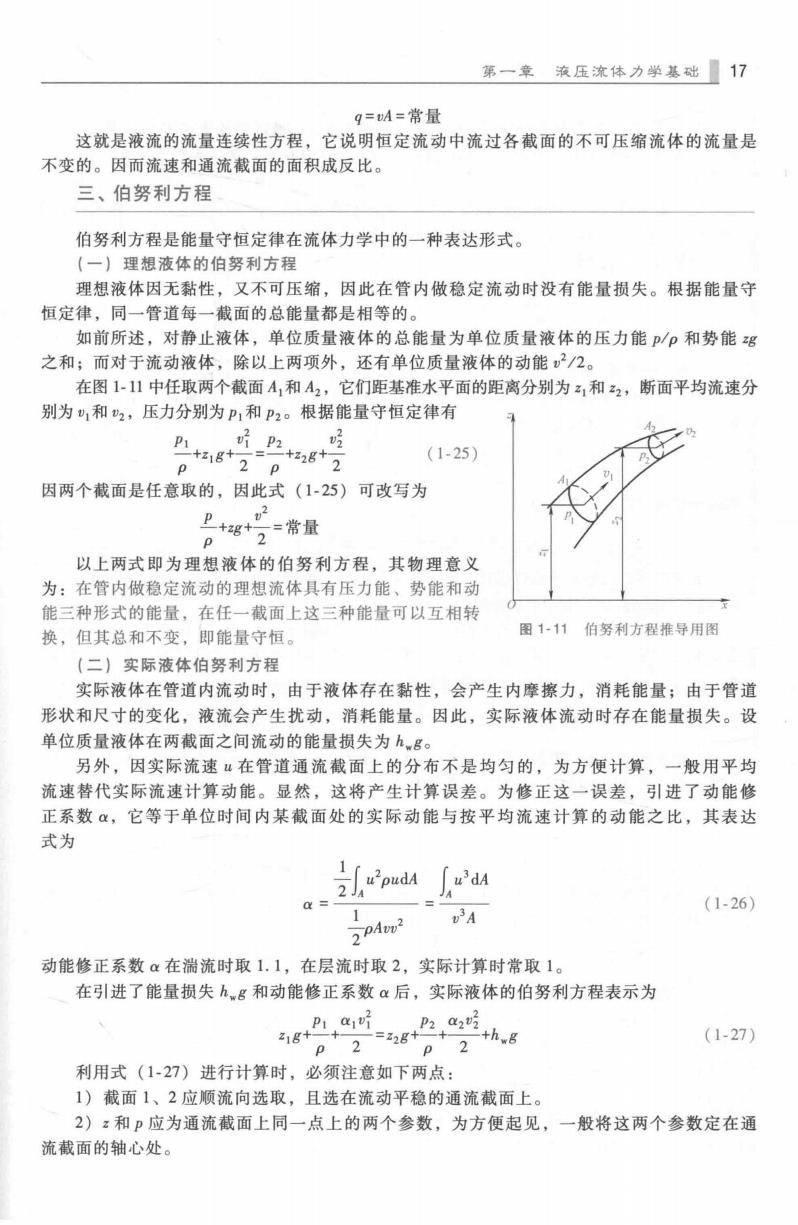
第一章液压流体力学基础【17 g=A=常量 这就是液流的流量连续性方程,它说明恒定流动中流过各截面的不可压缩流体的流量是 不变的。因而流速和通流截面的面积成反比。 三、伯努利方程 伯努利方程是能量守恒定律在流体力学中的一种表达形式。 (一)理想液体的伯努利方程 理想液体因无黏性,又不可压缩,因此在管内做稳定流动时没有能量损失。根据能量守 恒定律,同一管道每一截面的总能量都是相等的。 如前所述,对静止液体,单位质量液体的总能量为单位质量液体的压力能p/ρ和势能g 之和;而对于流动液体,除以上两项外,还有单位质量液体的动能2/2。 在图1-11中任取两个截面A,和A2,它们距基准水平面的距离分别为z1和22,断面平均流速分 别为和2,压力分别为P1和P2。根据能量守恒定律有 P1P2, t18+2。t28+2 (1-25) p 因两个截面是任意取的,因此式(1-25)可改写为 g号帝层 p 以上两式即为理想液体的伯努利方程,其物理意义 为:在管内做稳定流动的理想流体具有压力能、势能和动 能三种形式的能量,在任一截面上这三种能量可以互相转 换,但其总和不变,即能量守恒。 图1-11伯努利方程推导用图 (二)实际液体伯努利方程 实际液体在管道内流动时,由于液体存在黏性,会产生内摩擦力,消耗能量;由于管道 形状和尺寸的变化,液流会产生扰动,消耗能量。因此,实际液体流动时存在能量损失。设 单位质量液体在两截面之间流动的能量损失为h,g。 另外,因实际流速“在管道通流截面上的分布不是均匀的,为方便计算,一般用平均 流速替代实际流速计算动能。显然,这将产生计算误差。为修正这一误差,引进了动能修 正系数α,它等于单位时间内某截面处的实际动能与按平均流速计算的动能之比,其表达 式为 u'pudA a= (1-26) 2PAvy2 1 动能修正系数:在湍流时取1.1,在层流时取2,实际计算时常取1。 在引进了能量损失.g和动能修正系数:后,实际液体的伯努利方程表示为 P1 a P2 a p22g+2+ z1g+一+ P 2 二+h.g (1-27) 利用式(1-27)进行计算时,必须注意如下两点: 1)截面1、2应顺流向选取,且选在流动平稳的通流截面上。 2)z和p应为通流截面上同一点上的两个参数,为方便起见,一般将这两个参数定在通 流截面的轴心处
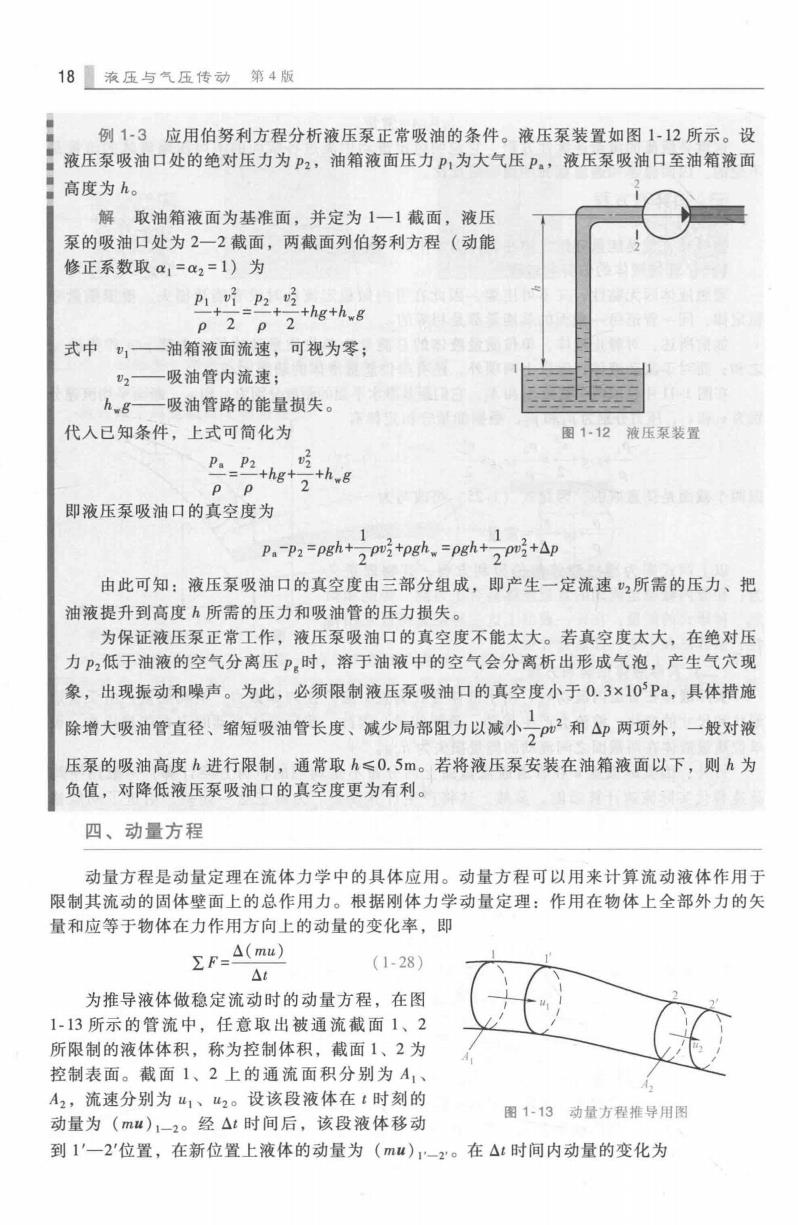
18液压与气压传动第4版 ● 例1-3应用伯努利方程分析液压泵正常吸油的条件。液压泵装置如图1-12所示。设 ◆ 液压泵吸油口处的绝对压力为P2,油箱液面压力P1为大气压P。,液压泵吸油口至油箱液面 高度为h。 解取油箱液面为基准面,并定为1一1截面,液压 泵的吸油口处为2一2截面,两截面列伯努利方程(动能 修正系数取a1=c2=1)为 p1Pp2吃 -=-+。+hg+hwg P 2 p 2 式中,一油箱液面流速,可视为零; 02- 吸油管内流速; h,g—吸油管路的能量损失。 代人已知条件,上式可简化为 图1-12液压泵装置 卫e2+hg*2h8 PP 即液压泵吸油口的真空度为 PPpghpghp 1 由此可知:液压泵吸油口的真空度由三部分组成,即产生一定流速2所需的压力、把 油液提升到高度h所需的压力和吸油管的压力损失。 为保证液压泵正常工作,液压泵吸油口的真空度不能太大。若真空度太大,在绝对压 力P2低于油液的空气分离压P,时,溶于油液中的空气会分离析出形成气泡,产生气穴现 象,出现振动和噪声。为此,必须限制液压泵吸油口的真空度小于0.3×10Pa,具体措施 除增大吸油管直径、缩短吸油管长度、减少局部阻力以减小22和4p两项外,一般对液 压泵的吸油高度h进行限制,通常取h≤0.5m。若将液压泵安装在油箱液面以下,则h为 负值,对降低液压泵吸油口的真空度更为有利。 四、动量方程 动量方程是动量定理在流体力学中的具体应用。动量方程可以用来计算流动液体作用于 限制其流动的固体壁面上的总作用力。根据刚体力学动量定理:作用在物体上全部外力的矢 量和应等于物体在力作用方向上的动量的变化率,即 ∑F=4(mu) (1-28) △t 为推导液体做稳定流动时的动量方程,在图 1-13所示的管流中,任意取出被通流截面1、2 所限制的液体体积,称为控制体积,截面1、2为 控制表面。截面1、2上的通流面积分别为A1、 A2,流速分别为山1、“2。设该段液体在t时刻的 图1-13动量方程推导用图 动量为(mu)1-2。经△t时间后,该段液体移动 到1'一2'位置,在新位置上液体的动量为(m4)1-2”。在△t时间内动量的变化为

第一章液压流体力学基础19 △(mu)=(m4)1-2-(mu)1-2 而 (mu)1-2=(m)1-+(mu)1-2 (mu)1-2=(mu)1-2+(mu)2-2x 如果液体做稳定流动,则1'一2之间液体的各点流速经△:后没有变化,动量也没有变 化,故 △(mu)=(mu)1-2-(mu)1-2 =(mu)2-2-(mu)1- =p9△tu2-pg△tu1 于是 ∑F=4(mu) =pg(42-u1) (1-29】 △t 式(1-29)为液体做稳定流动时的动量方程。方程表明:作用在液体控制体积上的外力 总和等于单位时间内流出控制表面与流入控制表面的液体的动量之差。该式为矢量表达式, 在应用时可根据具体要求,向指定方向投影,求得该方向的分量。显然,根据作用力与反作 用力相等原理,液体也以同样大小的力作用在使其流速发生变化的物体上。由此,可按动量 方程求得流动液体作用在固体壁面上的作用力。其中,由于液体稳定流动而引起液体对固体 壁面的附加作用力,称为稳态液动力。 ■ 例1-4图1-14为一滑阀示意图。当液流 通过滑阀时,试求液流对阀芯的轴向作用力。 解取阀进出口之间的液体为控制体积。 设液流做稳定流动,则作用在此控制体积内液 体上的力按式(1-29)应为 F=pq(v2cos02-v1C0s01) 式中01、02一液流流经滑阀时进、出口流 图1-14滑阀上的液动力 束与滑阀轴线之间的夹角,称为液流速度方 向角。 显然,无论是流入还是流出,2与滑阀轴线之间的夹角02=90°。由此可得F= pq吧1cos01,方向向左。而液体对阀芯的轴向作用力F'=-F=pgv1cos01,方向向右,即这时 液流有一个力图使阀口关闭的稳态液动力。 例1-5图1-15所示为一锥阀,其锥角为2a。液体在压力p的作 用下以流量q流经锥阀,求作用在阀芯上的稳态液动力的大小和方向。 解取阀口下方阴影部分为控制体,并假定控制体之外低压区 (P2=0)的流动液体对阀芯的作用力可忽略不计。 设阀芯对控制体的作用力为F,流入速度为1,流出速度为2, 则沿液流方向列出动量方程为 F(c00c0) 因为12,故可忽略1;02=a,01=0°,代人上式整理后得 Fpco 图1-15锥阀上的液动力

20液压与气压传动第4版 则液体作用在阀芯上的力F'为 F'=pqv2cosa- 从上述结果可知,一Pp为液体作用在阀芯上的液压力,方向向上:P9,60a为液体 稳定流动时作用在阀芯上的稳态液动力,方向向下,该力使阀口趋于关闭。 第四节管道流动 由于流动液体具有黏性,以及液体流动时突然转弯和通过阀口会产生相互撞击和出现漩 涡等,液体在管道中流动时必然会产生阻力。为了克服阻力,液体流动时需要损耗一部分能 量。这种能量损失可用液体的压力损失来表示。压力损失即伯努利方程中的gh项,它由沿 程压力损失和局部压力损失两部分组成。 液体在管路中流动时的压力损失和液体的运动状态有关,下面先分析液体的流态,然后 分析两类压力损失。 一、流态与雷诺数 (一)流态 英国物理学家雷诺通过大量实验,发现了液体在管道中流动时存在两种流动状态,即层 流和湍流。两种流动状态可通过雷诺实验来观察。 实验装置如图1-16a所示。容器6和3中分别装满了水和密度与水相同的红色液体,容器 6由水管2供水,并由溢流管1保持液面高度不变。打开阀门8让水从玻璃管7中流出,这时 打开阀门4,红色液体也经细导管5流入水平玻璃管7中。调节阀门8使玻璃管7中的流速较 小时,红色液体在玻璃管7中呈一条明显的直线,将细导管5的出口上下移动,则红色直线 也上下移动,而且这条红线和清水层次分明不相混杂,如图1-16b所示。液体的这种流动状 态称为层流。当调整阀门8使玻璃管中的流速逐渐增大至某一值时,可以看到红线开始出现 抖动而呈波纹状,如图1-16c所示。这表明层流状态被破坏,液流开始出现紊乱。若玻璃管7 中流速继续增大,红线消失,红色液体便和清水完全混杂在一起,如图1-16d所示。表明管 中液流完全湍乱,这时的流动状态称为湍流。如果将阀门8逐渐关小,当流速减小至一定值 时,水流又重新恢复为层流。 b c) d 图1-16雷诺实验装置(扫描二维码获得原理动画) 1一溢流管2一水管3、6一容器4、8一阀门5一细导管7一玻璃管
第一章液压流体力学基础21 层流与湍流是两种不同性质的流动状态。层流时液体流速较低,液体质点间的黏性力起 主导作用,液体质点受黏性力的约束,不能随意运动;湍流时液体流速较高,液体质点间黏 性力的制约作用减弱,惯性力起主导作用。 (二)雷诺数 液体的流动状态可用雷诺数来判断。 实验结果证明,液体在圆管中的流动状态不仅与管内的平均流速有关,还与管道内径 d、液体的运动黏度v有关。而用来判别液流状态的是由这三个参数所组成的一个无量纲 数—雷诺数Reo Re=vd (1-30) 雷诺数的物理意义表示了液体流动时惯性力与黏性力之比。如果液流的雷诺数相同,则 流动状态也相同。 液流由层流转变为湍流时的雷诺数与由湍流转变为层流时的雷诺数是不相同的,后者的 数值小,所以一般都用后者作为判别液流状态的依据,称为临界雷诺数,记为Re。。当液流的 实际雷诺数R小于临界雷诺数Re。时,为层流;反之,为湍流。常见液流管道的临界雷诺数 由实验求得,见表1-5。 表1-5常见液流管道的临界雷诺数 管道 Rea 管道 Recr 光滑金属圆管 2320 带环槽的同心环状缝隙 700 橡胶软管 1600-2000 带环槽的偏心环状缝隙 400 光滑的同心环状缝隙 1100 圆柱形滑阀阀口 260 光滑的偏心环状缝歇 1000 锥阀阀口 20-100 对于非圆截面的管道来说,Re可由下式计算 Re=4vR (1-31) v 式(1-31)中的R为通流截面的水力半径,它等于液流的有效面积A和它的湿周(有效截面 的周界长度)x之比,即 A R= (1-32) 水力半径的大小对管道的通流能力的影响很大。在流通截面面积A一定时,水力半径R大, 表示液流和管壁的接触周长短,管壁对液流的阻力小,通流能力大。在面积相等但形状不同 的所有通流截面中,圆形管道的水力半径最大。 二、圆管流动的沿程压力损失 液体在等直径圆管中流动时因黏性摩擦而产生的压力损失称为沿程压力损失。它不仅取 决于管道长度、直径及液体的黏度,而且与流体的流动状态即雷诺数有关,因此实际分析计 算时应先判别液体的流态是层流还是湍流。 (一)层流时的沿程压力损失 液流在层流流动时,液体质点做有规则的运动,因此可以方便地用数学工具来分析液流 的速度、流量和压力损失。 1.通流截面上的流速分布规律 在图1-17中,液体在等径水平圆管中做层流运动。在液流中取一段与圆管轴线相重合的