
第一章液压流体力学基础27 3)在孔口通流面积A一定时,改变流经孔口的流量,孔口压降△p随之变化。这种特性 为液阻的阻力特性,一般用于压力控制阀的内部控制。 11 4)当多个孔口串联时,总液阻R=∑R;当多个孔口并联时,总液阻R R R2 第六节缝隙流动 在液压元件中,构成运动副的一些运动件与固定件之间存在着一定缝隙,而当缝隙两端 的液体存在压差时,势必形成缝隙流动,即泄漏。泄漏的存在将严重影响液压元件,特别是 液压泵和液压马达的工作性能。当圆柱体存在一定锥度时,其缝隙流动还可能导致卡紧现象, 这是一个需要引起注意的问题。 一、平板缝隙 当两平行平板缝隙间充满液体时,如果液体受到压差△p=P1-P2的作用,液体会产生流 动。如果没有压差△p的作用,而两平行平板之间有相对 运动,即一平板固定,另一平板以速度4。(与压差方向相 同)运动时,由于液体存在黏性,液体也会被带着移动, t+dt 这就是剪切作用所引起的流动。液体通过平行平板缝隙时 p+dp 的最一般的流动情况,是既受压差△p的作用,又受平行 平板相对运动的作用,如图1-24所示。 图1-24中h为缝隙高度,b和I分别为缝隙宽度和长 度,一般b>>h,l>>h。在液流中取一个微元体dxdy(宽 度方向取单位长),其左右两端面所受的压力分别为p和P +dp,上下两面所受的切应力分别为T+dr和r,则微元体 的受力平衡方程为 图1-24平行平板缝隙间的液流 pdy+(r+dr)dx=(p+dp)dy+rdx 整理后得 drdp dy dx du 由于以西上式可变为 d2u 1 dp dy2μdx 将上式对y积分两次得 1 dp2+C1y+C2 u= 2μdx 上式中C1、C2为积分常数。当平行平板间的相对运动速度为时,在y=0处,u=0;在y=h 处,u=uo。此外,液流做层流运动时p只是x的线性函数,即dp/dx=(P2P1)/儿=-△p/L,将 这些关系式代入上式并整理后得 =y(h-y)ap (1-50) 2μl 由此得到通过平行平板缝隙的流量为
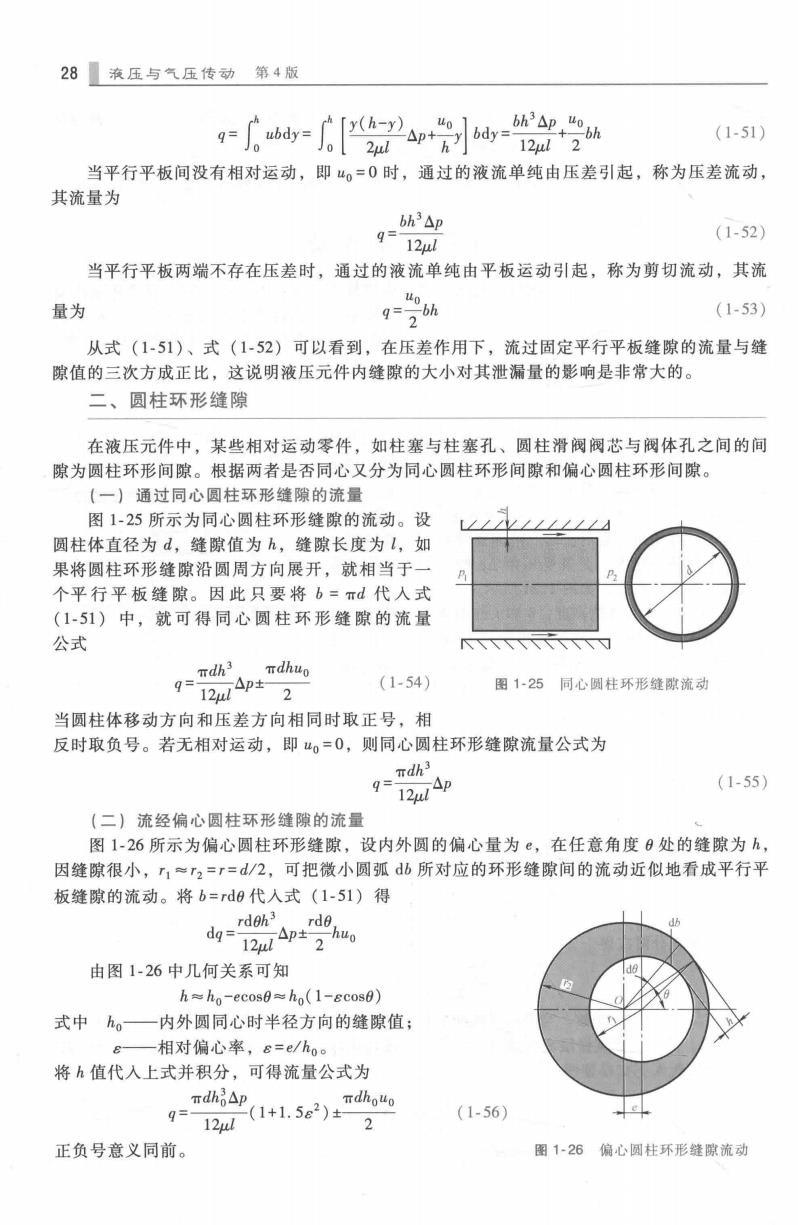
28液压与气压传动第4版 ,=bh△P,0bh (1-51) 12ul2 当平行平板间没有相对运动,即“0=0时,通过的液流单纯由压差引起,称为压差流动, 其流量为 bh3△p q=12μ (1-52) 当平行平板两端不存在压差时,通过的液流单纯由平板运动引起,称为剪切流动,其流 量为 (1-53) 从式(1-51)、式(1-52)可以看到,在压差作用下,流过固定平行平板缝隙的流量与缝 隙值的三次方成正比,这说明液压元件内缝隙的大小对其泄漏量的影响是非常大的。 二、圆柱环形缝隙 在液压元件中,某些相对运动零件,如柱塞与柱塞孔、圆柱滑阀阀芯与阀体孔之间的间 隙为圆柱环形间隙。根据两者是否同心又分为同心圆柱环形间隙和偏心圆柱环形间隙。 (一)通过同心圆柱环形缝隙的流量 图1-25所示为同心圆柱环形缝隙的流动。设 圆柱体直径为d,缝隙值为h,缝隙长度为l,如 果将圆柱环形缝隙沿圆周方向展开,就相当于一 个平行平板缝隙。因此只要将b=πd代人式 (1-51)中,就可得同心圆柱环形缝隙的流量 公式 Tdh3 Tdhuo 9= △p士 (1-54) 12μl 2 图1-25同心圆柱环形缝隙流动 当圆柱体移动方向和压差方向相同时取正号,相 反时取负号。若无相对运动,即uo=0,则同心圆柱环形缝隙流量公式为 9=mdhs 12ulAp (1-55) (二)流经偏心圆柱环形缝隙的流量 图1-26所示为偏心圆柱环形缝隙,设内外圆的偏心量为e,在任意角度0处的缝隙为h, 因缝隙很小,1≈T2=r=d/2,可把微小圆弧db所对应的环形缝隙间的流动近似地看成平行平 板缝隙的流动。将b=rd0代入式(1-51)得 rdeh3 rde dq = huo 12μl p±2 由图1-26中几何关系可知 h≈ho-ecos0≈ho(1-Ecos0) 式中。一内外圆同心时半径方向的缝隙值; e一相对偏心率,B=e/hoo 将h值代入上式并积分,可得流量公式为 πdh△p, 9=12d(1+1.562)± dhouo 2 (1-56) 正负号意义同前。 图1-26偏心圆柱环形缝隙流动

第一章液压流体力学基础29 当内外圆之间没有轴向相对移动,即“,=0时,其流量为 rdh△ (1+1.5e2) (1-57) 124l 由式(1-57)可以看出,当偏心量e=ho,即ε=1时(最大偏心状态),其通过的流量是同心圆柱 环形缝隙的2.5倍。因此在液压元件中,有配合的零件应尽量使其同心,以减小缝隙泄漏量。 三、圆锥环形间隙 当柱塞或柱塞孔、阀芯或阀体孔因加工误差带有一定锥度时,两相对运动零件之间的间 隙为圆锥环形间隙,其间隙大 小沿轴线方向变化。图1-27a所 示阀芯大端为高压,液流由大 端流向小端,称为倒锥;图 1-27b所示阀芯小端为高压,液 流由小端流向大端,称为顺锥。 阀芯存在锥度不仅影响流经间 隙的流量,而且影响缝隙中的 b) 压力分布。 图1-27圆锥环形间隙的液流 设圆锥半角为0,阀芯以速 a)倒锥b)顺锥 度向右移动,进出口处的缝 隙和压力分别为h1、P1和h2、P2,并设距左端面x距离处的缝隙为h,压力为P,则在微小单 元dx处的流动,由于dx值很小而认为dx段内缝隙宽度不变。 对于图1·27所示的流动情况,由于中-,将其代人同心圆柱环形缝隙流量公式(① 54)得 wdh dp Tduoh 9= 12μdx2 由于h=h1 +xtand0,dk=dh 代入上式并整理后得 12gdh6μuo,dh dp = (1-58) Tdtan0h3 tan h2 对上式进行积分,并将tan0=(h2-h,)/L代入后得 6ul(h1+h2)_6ul △p=P1-P2= u0 d (hha)h 将上式移项可求出环形圆锥缝隙的流量公式为 ad (hh2)2 dh1h2 Gul(h th)p+ 9= 1+h2)40 (1-59) 当阀芯没有运动,即o=0时,流量公式为 ad(hh2)2 6u1(h,+h)4p (1-60) 四、液压卡紧现象 若对式(1-58)积分,并将边界条件h=h1、p=P1代入,可得圆锥环形间隙中的压力分
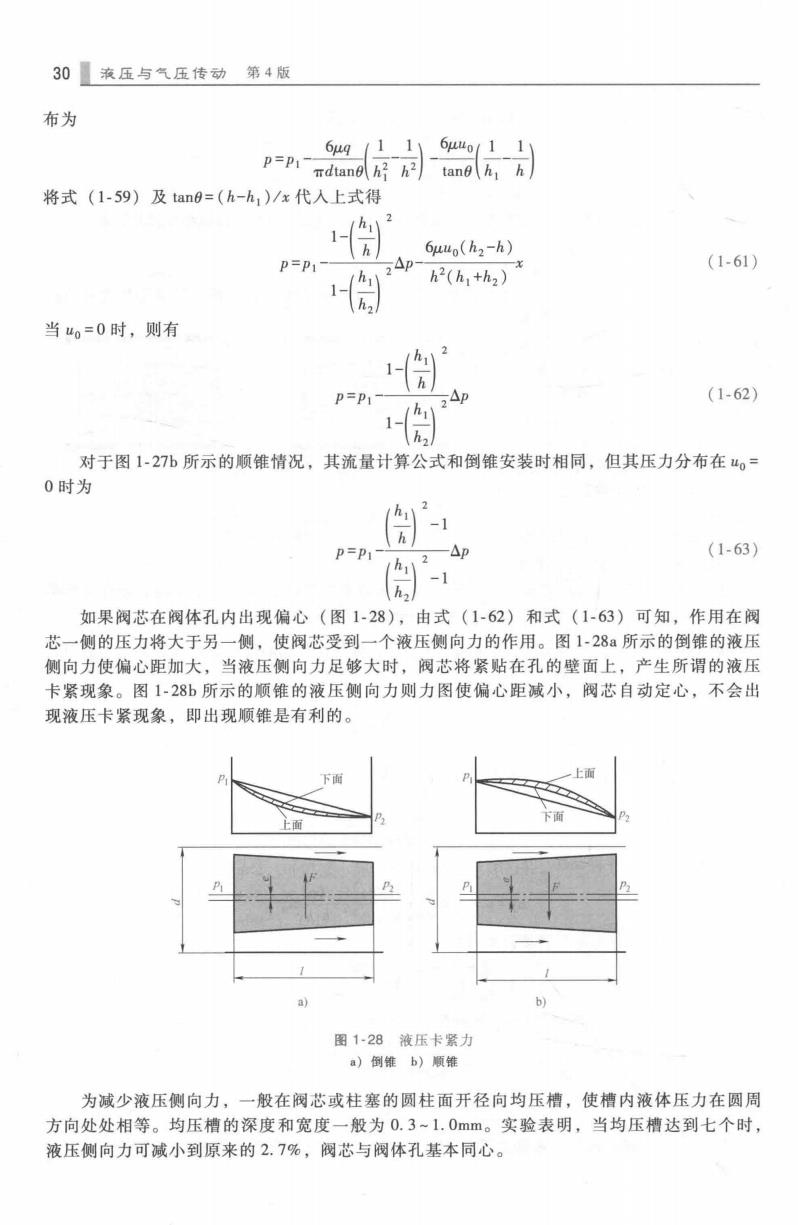
30■液压与气压传动第4版 布为 6μg/111 6μuo11 p=PI- dtanh好h2 将式(1-59)及tan0=(h-h,)/x代入上式得 2 6uuo(h2-h) P=P1 △p (1-61) h2(h1+h2) 当uo=0时,则有 1- P=P1 (1-62) h 对于图1-27b所示的顺锥情况,其流量计算公式和倒锥安装时相同,但其压力分布在0= 0时为 -1 P=PI -△p (1-63) h -1 如果阀芯在阀体孔内出现偏心(图1-28),由式(1-62)和式(1-63)可知,作用在阀 芯一侧的压力将大于另一侧,使阀芯受到一个液压侧向力的作用。图1-28所示的倒锥的液压 侧向力使偏心距加大,当液压侧向力足够大时,阀芯将紧贴在孔的壁面上,产生所谓的液压 卡紧现象。图1-28b所示的顺锥的液压侧向力则力图使偏心距减小,阀芯自动定心,不会出 现液压卡紧现象,即出现顺锥是有利的。 下面 上而 上面 a) 图1-28液压卡紧力 a)倒锥b)顺锥 为减少液压侧向力,一般在阀芯或柱塞的圆柱面开径向均压槽,使槽内液体压力在圆周 方向处处相等。均压槽的深度和宽度一般为0.3~1.0mm。实验表明,当均压槽达到七个时, 液压侧向力可减小到原来的2.7%,阀芯与阀体孔基本同心

第一章液压流体力学基础31 当然,在开设径向均压槽后,环形缝隙的长度会减小,但由于均压槽会使阀芯与阀体孔 之间的偏心距减小,因此,均压槽的开设不会使缝隙的泄漏量增大。 第七节液压冲击和气穴现象 在液压传动中,液压冲击和气穴现象都会给液压系统的正常工作带来不利影响,因此需 要了解这些现象产生的原因,并采取相应的措施以减小其危害。 一、液压冲击 在液压系统中,因某些原因液体压力在一瞬间会突然升高,产生很高的压力峰值,这种 现象称为液压冲击。液压冲击的压力峰值往往比正常工作压力高好几倍,瞬间压力冲击不仅 引起振动和噪声,而且会损坏密封装置、管道和液压元件,有时还会使某些液压元件(如压 力继电器、顺序阀等)产生误动作,造成设备事故。 (一)液压冲击的类型 液压系统中的液压冲击按其产生的原因分为:①因液流通道迅速关闭或液流迅速换向使 液流速度的大小或方向发生突然变化时,液流的惯性导致的液压冲击:②运动的工作部件突 然制动或换向时,因工作部件的惯性引起的液压冲击。下面对两种常见的液压冲击现象进行 分析。 1.管道阀门突然关闭时的液压冲击 在图1-29中,具有一定容积的容器(蓄能器或液压缸)中的液体沿长度为1、直径为d 的管道经出口处的阀门以速度流出。若将阀门突然 关闭,则在靠近阀门处B点处的液体立即停止运动, 液体的动能转换为压力能,B点处的压力升高△p,接 着后面的液体分层依次停止运动,动能依次转换为压 力能,形成压力波,并以速度c由B向A传播,到A 点后,又反向向B点传播。于是,压力冲击波以速度c 在管道的A、B两点间往复传播,在系统内形成压力振 荡。实际上由于管道变形和液体黏性损失需要消耗能 量,因此振荡过程逐渐衰减,最后趋于稳定。 下面来计算阀门迅速关闭时的最大压力升高值△p。 图1-29管道中的液压冲击 设管路截面面积为A,管长为I,压力波从B点传递到A 点的时间为,液体密度为ρ,管道中液流速度为。,阀门关闭后的流速为零,则由动量方程得 ApA=pA t △p=p,0=pc0 (1-64) 式中,c=/:为压力冲击波在管中的传播速度,其不仅与液体的体积弹性模量K有关,还和管 道材料的弹性模量E、管道的内径d及管道壁厚8有关。c值可按下式计算 (1-65) Kd E8