复旦大学：《统计热力学》课程教学资源（课件讲稿）06 统计热力学的应用——多原子分子转动，内转动

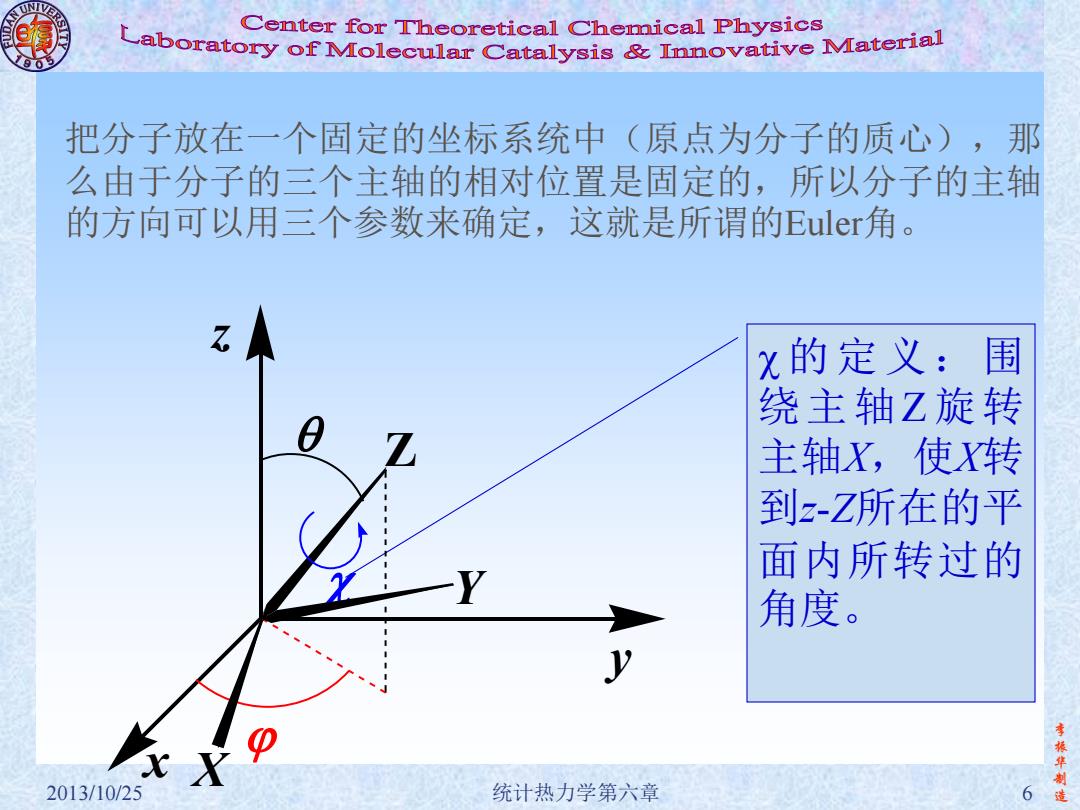
Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 把分子放在一个固定的坐标系统中 (原点为分子的质心)，那 么由于分子的三个主轴的相对位置是固定的，所以分子的主轴 的方向可以用三个参数来确定，这就是所谓的Euler角。 x的定义：围 绕主轴Z旋转 主轴X,使X转 到z-Z所在的平 面内所转过的 角度。 李振华制 2013/10/25 统计热力学第六章 6

李 振 华 制 2013/10/25 统计热力学第六章 6 造 把分子放在一个固定的坐标系统中（原点为分子的质心），那 么由于分子的三个主轴的相对位置是固定的，所以分子的主轴 的方向可以用三个参数来确定，这就是所谓的Euler角。 c的定义：围 绕主轴Z旋转 主轴X，使X转 到z-Z所在的平 面内所转过的 角度。 Z z x y   c X Y

Center for Theoretical Chemical Physics of Molecular Catalysis mnov 根据经典力学，转动动能为： 22,pz = 24 2B 2C 其中： (,co0) 2=A57名n-A,eo0j P2P和p分别是X,p和对应的共轭动量。 李振华 2013/10/25 统计热力学第六章 造

李 振 华 制 2013/10/25 统计热力学第六章 7 造 根据经典力学，转动动能为： C p A B r 2 2 2 2 2 2   c     其中： ( cos ) sin sin cos ( cos ) sin cos sin   c  c   c  c   c   c p p p p p p       pc , p和p分别是c, 和对应的共轭动量

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 那么转动配分函数为： r方ie心a电，aa 如果能够把上式中对p和pg的积分转化为对y和λ的积 分就简单了。因为转化后积分项很可能就是： 2AkT dy 对积分空间的转化实际上就是把坐标系从原来的p, pp名p,变换为Y,入，p2名，p,0。实际上只是 对两维坐标作了变换。 振华制 2013/10/25 统计热力学第六章 8

李 振 华 制 2013/10/25 统计热力学第六章 8 造 那么转动配分函数为：          c   c   e dp dp dp d d d h dΓ Γ e q k T k T r r B r B / 3 / 1 如果能够把上式中对p和p的积分转化为对γ和λ的积 分就简单了。因为转化后积分项很可能就是：     e d 2AkB T 2 对积分空间的转化实际上就是把坐标系从原来的p , p , pc , c, ，变换为，， pc , c, ，。实际上只是 对两维坐标作了变换

Center for Theoretical Chemical Physics aboratory of Molecular Catalysis Innovative Materia 坐标变换的一般讨论 坐标变换后，空间中的体积元在变换前后有一个比 例系数，这个系数是以Jacobian(雅可比)行列式 的形式来表示的 dl"Jdl 行列式的维度等于空间的维 度。对于三维的坐标变换： dxdx,dx;=Ida dada; 武就武就武就 振华 2013/10/25 统计热力学第六章 造

李 振 华 制 2013/10/25 统计热力学第六章 9 造 坐标变换的一般讨论  坐标变换后，空间中的体积元在变换前后有一个比 例系数，这个系数是以Jacobian（雅可比）行列式 的形式来表示的： dΓ  JdΓ' 3 3 3 2 3 1 2 3 2 2 2 1 1 3 1 2 1 1 a x a x a x a x a x a x a x a x a x J                    行列式的维度等于空间的维 度。对于三维的坐标变换： 1 2 3 1 da2 da3 dx dx dx  Jda

Center for Theoretical Chemical Physics Laboratory of Molecular Catalysis mnovative Material 一般表示为： J= O(x1,x2,X3） a(a1,a2,a3） 直角坐标到球坐标的变换 dxdydz=r-sin Odrdedo 在这里： dyd=Jdpodp aλ ope 元 op. opo 李振华制 2013/10/25 统计热力学第六章 10

李 振 华 制 2013/10/25 统计热力学第六章 10 造 一般表示为： 在这里： dxdydz r sindrdd 2  直角坐标到球坐标的变换 ( , , ) ( , , ) 1 2 3 1 2 3 a a a x x x J            p p p p J             dd  Jdp dp