白)几何意义 「f(x)d=F(x)+c y↑ y=F(x)+C ↑y=F(x) X 曲线y=F(x)称为函数f(x)的积分曲线。 y=F(x)+c为积分曲线簇。 8
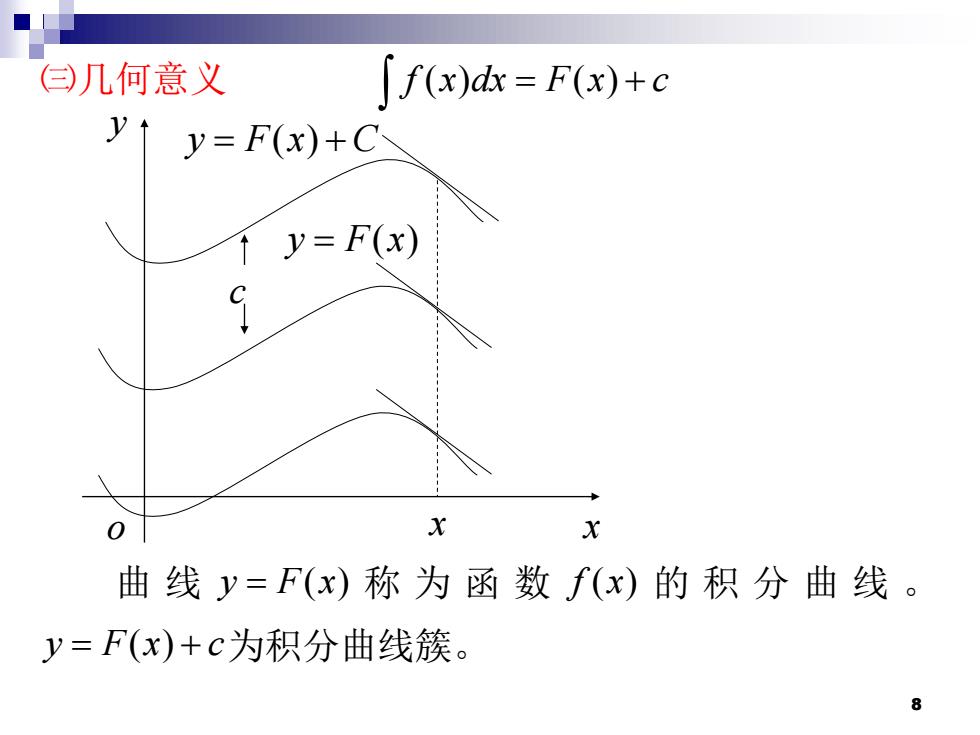
8 ㈢几何意义 f x dx F x c ( ) ( ) = + 曲 线 y F x = ( ) 称 为 函 数 f x( ) 的 积 分 曲 线 。 y F x c = + ( ) 为积分曲线簇。 y o x y F x C = + ( ) y F x = ( ) c x

例1.求sinxd。 解 因为 (-cosx)'=sinx 所以 [sinxdx=-cosx+c 例2.求经过(1,3)点,且其任意一点(x,y)处的 切线的斜率为3x2的曲线方程。 解设曲线方程y=F(x),则F'(x)=3x2 因为 (x3)'=3x2 所以F(x)=「3x2d=x3+c 得曲线族y=x3+c 将x=1,y=3代入得C=2。故所求曲线为y=x3+2。 9
9 例1. 求 sin xdx 。 解 因为 ( cos )' sin − = x x 所以 sin cos xdx x c = − + 例2. 求经过(1,3)点,且其任意一点( , ) x y 处的 切线的斜率为 2 3x 的曲线方程。 解 设曲线方程y F x = ( ),则 2 F x x ( ) 3 = 因为 3 2 ( )' 3 x x = 所以 2 3 F x x dx x c ( ) 3 = = + 得曲线族 3 y x c = + 将x y = = 1, 3代入得c = 2。故所求曲线为 3 y x = + 2

二、不定积分的性质和基本积分公式 性质1(f(x)ax)'=f(x) 或 d f(x)dx=f(x)dx 证 设F'(x)=f(x),则 f(x)dx=F(x)+c 故 (f(x))'=(F(x)+c)'=F'(x)=f(x) 而 d f(x)dx=(f(x)dx)'dx=f(x)dx 性质2」∫'(x)c=f(x)+c或d(x)=f(x)+c 证因(f(x)'='(x)故f(x)为f'(x)的原函数。则 ∫f'(x)=f(x)+c,从而∫df(x)=∫f(x)dk=f(x)+c 10
10 二、不定积分的性质和基本积分公式 性质 1 ( ( ) )' ( ) f x dx f x = 或 d f x dx f x dx ( ) ( ) = 证 设F x f x '( ) ( ) = ,则 f x dx F x c ( ) ( ) = + 故 ( ( ) )' ( ( ) )' '( ) ( ) f x dx F x c F x f x = + = = 而 d f x dx f x dx dx f x dx ( ) ( ( ) )' ( ) = = 性质 2 f x dx f x c '( ) ( ) = + 或 df x f x c ( ) ( ) = + 证 因 ( ( ))' '( ) f x f x = 故 f x( ) 为 f x'( ) 的 原 函 数 。 则 f x dx f x c '( ) ( ) = + ,从而 df x f x dx f x c ( ) '( ) ( ) = = +