
2.本课程支撑的指标点:指标点1.1、1.2、1.3、1.4、2.1、2.2 (1)指标点11:能将数学、自然科学、工程基础和专业知识用到复杂工程问题的恰当表述中。 (2)指标点1.2:能针对一个系统或者过程建立合适的数学模型,并利用恰当的方式求解。 (3)指标点1.3:能将专业知识和数学模型的方法用于分析、判别过程的极限和优化途径。 (4)指标点1.4:能用专业知识,通过模型比较和综合,优选工程问题的解决方案,完成系 统的设计和计算。 (5)指标点2.1:能识别和判断复杂工程问题的关键环节和参数。 (6)指标点2.2:能基于科学原理和数学模型方法正确表达工程问题的解决方案。 (三)课程教学目标与半业要求对应表 《复变函数与积分变换》课程教学目标与半业要求的对应表 课程名称:复变函数与积分变换 任课教师:彭兴媛,王晋 课程性质:学科必修课 课程学分:2.5 课程支撑的半业要求 课程目标、达成途径、评价依据 毕业要求1:具备良好的工程知 教学目标1:使学生掌握复变函数与积分变换的基础理 识,能够将数学、自然科学、工 论和运算技能。 程基础和专业知识用于解决自动 达成途径:通过概念讲解使学生掌握复变函数与积分变 化控制系统、自动化测试系统开 换的重点知识、运算技能及应用方法,进而运用复变函 发或集成中的复杂工程问题; 数与积分变换的思想与方法对复杂工程问题进行恰当表 指标点11能将数学、自然科学、 述。 工程基础和专业知识用到复杂工 评价依据:课堂笔记、提问、作业和考试。 程问题的恰当表述中。 毕业要求1:具备良好的工程知 教学目标2:使学生可以学到数学物理及工程技术中常 识,能够将数学、自然科学、工 用的数学方法,能够运用所学知识分析复杂问题,并能 程基础和专业知识用于解决自动 够建立模型。 化控制系统、自动化测试系统开 达成途径:利用解析函数和调和函数的关系,利用调和 发或集成中的复杂工程问题: 函数构建解析函数,并利用偏积分法或线积分法进行求 指标点1.2能针对一个系统或者 解。 过程建立合适的数学模型,并利 评价依据:课堂笔记、提问、作业和考试。 用恰当的方式求解。 毕业要求1:具备良好的工程知 教学目标3:引导学生能应用专业知识用于判别计算过 识,能够将数学、自然科学、工 程的极限和优化方案 程基础和专业知识用于解决自动 达成途径:通过学习函数极限的概念,同时复习高等数 化控制系统、自动化测试系统开 学课程中有关实数域上的极限的知识,加深对极限思想 发或集成中的复杂工程问题; 的理解,并锻炼判断极限存在与否的能力。 指标点13能将专业知识和数学 评价依据:课堂笔记、提问、作业和考试。 模型的方法用于分析、判别过程 的极限和优化途径。 毕业要求1:具备良好的工程知 教学目标4:能应用间接法将函数进行泰勒或洛朗展开, 识,能够将数学、自然科学、工 并能利用留数解决复闭路积分、定积分和反常积分。 程基础和专业知识用于解决自动 达成途径:能计算幂级数的收敛半径及函数的泰勒展开, 化控制系统、自动化测试系统开 并能利用已知函数的泰勒展开式对所给函数进行洛朗展 33
33 2. 本课程支撑的指标点:指标点 1.1、1.2、1.3、1.4、2.1、2.2 (1)指标点 1.1: 能将数学、自然科学、工程基础和专业知识用到复杂工程问题的恰当表述中。 (2)指标点 1.2:能针对一个系统或者过程建立合适的数学模型,并利用恰当的方式求解。 (3)指标点 1.3:能将专业知识和数学模型的方法用于分析、判别过程的极限和优化途径。 (4)指标点 1.4:能用专业知识,通过模型比较和综合,优选工程问题的解决方案,完成系 统的设计和计算。 (5)指标点 2.1:能识别和判断复杂工程问题的关键环节和参数。 (6)指标点 2.2:能基于科学原理和数学模型方法正确表达工程问题的解决方案。 (三)课程教学目标与毕业要求对应表 《复变函数与积分变换》课程教学目标与毕业要求的对应表 课程名称:复变函数与积分变换 任课教师:彭兴媛,王晋 课程性质:学科必修课 课程学分:2.5 课程支撑的毕业要求 课程目标、达成途径、评价依据 毕业要求 1:具备良好的工程知 识,能够将数学、自然科学、工 程基础和专业知识用于解决自动 化控制系统、自动化测试系统开 发或集成中的复杂工程问题; 指标点 1.1 能将数学、自然科学、 工程基础和专业知识用到复杂工 程问题的恰当表述中。 教学目标 1:使学生掌握复变函数与积分变换的基础理 论和运算技能。 达成途径:通过概念讲解使学生掌握复变函数与积分变 换的重点知识、运算技能及应用方法,进而运用复变函 数与积分变换的思想与方法对复杂工程问题进行恰当表 述。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 1:具备良好的工程知 识,能够将数学、自然科学、工 程基础和专业知识用于解决自动 化控制系统、自动化测试系统开 发或集成中的复杂工程问题; 指标点 1.2 能针对一个系统或者 过程建立合适的数学模型,并利 用恰当的方式求解。 教学目标 2:使学生可以学到数学物理及工程技术中常 用的数学方法,能够运用所学知识分析复杂问题,并能 够建立模型。 达成途径:利用解析函数和调和函数的关系,利用调和 函数构建解析函数,并利用偏积分法或线积分法进行求 解。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 1:具备良好的工程知 识,能够将数学、自然科学、工 程基础和专业知识用于解决自动 化控制系统、自动化测试系统开 发或集成中的复杂工程问题; 指标点 1.3 能将专业知识和数学 模型的方法用于分析、判别过程 的极限和优化途径。 教学目标 3:引导学生能应用专业知识用于判别计算过 程的极限和优化方案 达成途径:通过学习函数极限的概念,同时复习高等数 学课程中有关实数域上的极限的知识,加深对极限思想 的理解,并锻炼判断极限存在与否的能力。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 1:具备良好的工程知 识,能够将数学、自然科学、工 程基础和专业知识用于解决自动 化控制系统、自动化测试系统开 教学目标 4:能应用间接法将函数进行泰勒或洛朗展开, 并能利用留数解决复闭路积分、定积分和反常积分。 达成途径:能计算幂级数的收敛半径及函数的泰勒展开, 并能利用已知函数的泰勒展开式对所给函数进行洛朗展

发或集成中的复杂工程问题: 开:能求出孤立奇点处的留数,进而给出利用围道积分 指标点1.4能用专业知识,通过 法对定积分和反常积分进行计算的方案。 模型比较和综合,优选工程问题 评价依据:课堂笔记、提问、作业和考试。 的解决方案,完成系统的设计和 计算。 毕业要求2:能够应用数学、自 教学目标5:引导学生能识别和判断计算过程中的关键 然科学和工程科学的基本原理, 环节和参数。 识别、表达、并通过文献研究分 达成途径:利用柯西定理、柯西积分公式及其推论确定 析自动化控制系统的复杂工程问 计算闭路积分的关键环节,并在利用参数方程法计算曲 题,以获得有效结论; 线积分时确定其关键参数。 指标点2.1能识别和判断复杂工 评价依据:课堂笔记、提问、作业和考试。 程问题的关键环节和参数。 毕业要求2:能够应用数学、自 教学目标6:通过积分变换的学习能提出问题的不同解 然科学和工程科学的基本原理, 决方案。 识别、表达、并通过文献研究分 达成途径:通过对傅立叶变换和拉普拉斯变换的学习, 析自动化控制系统的复杂工程问 能利用他们的性质建立解决微积分方程的方案。 题,以获得有效结论; 评价依据:课堂笔记、提问、作业和考试。 指标点2.2能基于科学原理和数 学模型方法正确表达工程问题的 解决方案。 四、课程内容 教学内容 作业要求 第一篇复变函数 自学内容:复数的定义及代数运算。 第一章复数与复变函数 1.1复数 课堂作业: 1.2复数的乘幂与方根 讨论实数和复数的区别 1.3平面点集 1.4复变函数 课外作业: 1.5初等函数 1完成本章小结 知识点: 2.练习复数的几种表示方法 1.复数的概念、运算及几何表示,扩充复平 3练习复数的四则运算 面 4练习复数的乘幂和方根的计算 2.复数的乘幂方根,共轭运算 3.复平面上区域、曲线的概念,单连通域, 多连通域。 4.复变函数的概念,几何解释,反函数与复 合函数定义。 5.复数域上的初等函数的定义与性质。 第二章导数 自学内容:复习高等数学中函数极限、连续、 2.1复变函数的极限 导数等概念 2.2复变函数的连续性 2.3导数 课堂作业: 2.4解析函数 讨论复变函数与实变函数的极限、连续、导 34
34 发或集成中的复杂工程问题; 指标点 1.4 能用专业知识,通过 模型比较和综合,优选工程问题 的解决方案,完成系统的设计和 计算。 开;能求出孤立奇点处的留数,进而给出利用围道积分 法对定积分和反常积分进行计算的方案。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 2:能够应用数学、自 然科学和工程科学的基本原理, 识别、表达、并通过文献研究分 析自动化控制系统的复杂工程问 题,以获得有效结论; 指标点 2.1 能识别和判断复杂工 程问题的关键环节和参数。 教学目标 5:引导学生能识别和判断计算过程中的关键 环节和参数。 达成途径:利用柯西定理、柯西积分公式及其推论确定 计算闭路积分的关键环节,并在利用参数方程法计算曲 线积分时确定其关键参数。 评价依据:课堂笔记、提问、作业和考试。 毕业要求 2:能够应用数学、自 然科学和工程科学的基本原理, 识别、表达、并通过文献研究分 析自动化控制系统的复杂工程问 题,以获得有效结论; 指标点 2.2 能基于科学原理和数 学模型方法正确表达工程问题的 解决方案。 教学目标 6:通过积分变换的学习能提出问题的不同解 决方案。 达成途径:通过对傅立叶变换和拉普拉斯变换的学习, 能利用他们的性质建立解决微积分方程的方案。 评价依据:课堂笔记、提问、作业和考试。 四、课程内容 教学内容 作业要求 第一篇 复变函数 第一章 复数与复变函数 1.1 复数 1.2 复数的乘幂与方根 1.3 平面点集 1.4 复变函数 1.5 初等函数 知识点: 1. 复数的概念、运算及几何表示,扩充复平 面 2. 复数的乘幂方根,共轭运算 3. 复平面上区域、曲线的概念,单连通域, 多连通域。 4. 复变函数的概念,几何解释,反函数与复 合函数定义。 5. 复数域上的初等函数的定义与性质。 自学内容:复数的定义及代数运算。 课堂作业: 讨论实数和复数的区别 课外作业: 1.完成本章小结 2.练习复数的几种表示方法 3.练习复数的四则运算 4.练习复数的乘幂和方根的计算 第二章 导数 2.1 复变函数的极限 2.2 复变函数的连续性 2.3 导数 2.4 解析函数 自学内容:复习高等数学中函数极限、连续、 导数等概念 课堂作业: 讨论复变函数与实变函数的极限、连续、导
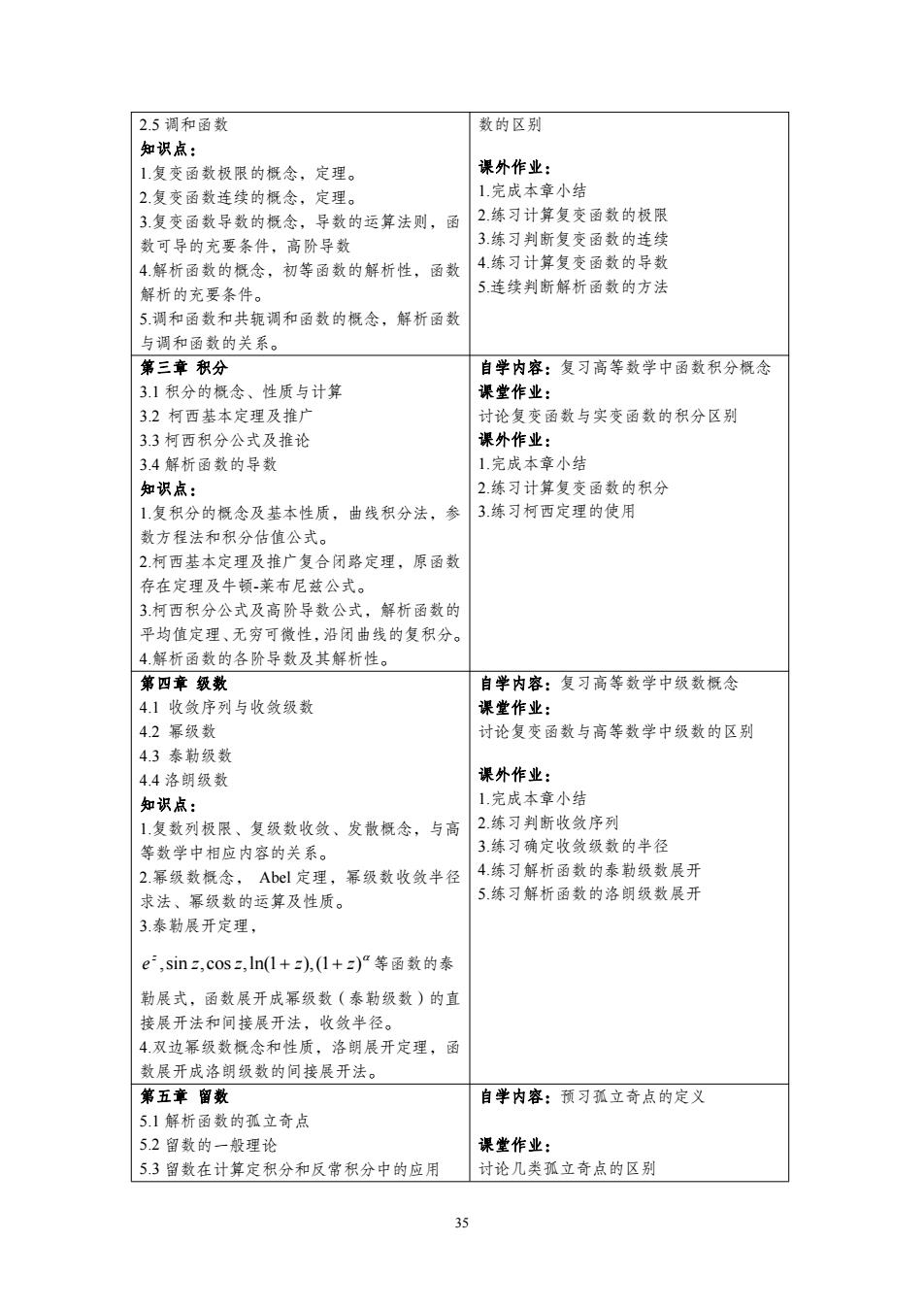
2.5调和函数 数的区别 知识点: 1复变函数极限的概念,定理。 课外作业: 2.复变函数连续的概念,定理。 1完成本章小结 3复变函数导数的概念,导数的运算法则,函 2.练习计算复变函数的极限 数可导的充要条件,高阶导数 3练习判断复变函数的连续 4.解析函数的概念,初等函数的解析性,函数 4.练习计算复变函数的导数 解析的充要条件。 5.连续判断解析函数的方法 5.调和函数和共轭调和函数的概念,解析函数 与调和函数的关系。 第三章积分 自学内容:复习高等数学中函数积分概念 3.1积分的概念、性质与计算 课堂作业: 32柯西基本定理及推广 讨论复变函数与实变函数的积分区别 3.3柯西积分公式及推论 课外作业: 3.4解析函数的导数 1.完成本章小结 知识点: 2.练习计算复变函数的积分 1.复积分的概念及基本性质,曲线积分法,参 3.练习柯西定理的使用 数方程法和积分估值公式。 2柯西基本定理及推广复合闭路定理,原函数 存在定理及牛顿-莱布尼兹公式。 3柯西积分公式及高阶导数公式,解析函数的 平均值定理、无穷可微性,沿闭曲线的复积分。 4解析函数的各阶导数及其解析性。 第四章级数 自学内容:复习高等数学中级数概念 4.1收敛序列与收敛级数 课堂作业: 4.2幂级数 讨论复变函数与高等数学中级数的区别 4.3泰勒级数 4.4洛朗级数 课外作业: 知识点: 1完成本章小结 1复数列极限、复级数收敛、发散概念,与高 2.练习判断收敛序列 等数学中相应内容的关系。 3.练习确定收敛级数的半径 2.幂级数概念,Abel定理,幂级数收敛半径 4.练习解析函数的泰勒级数展开 求法、幂级数的运算及性质。 5.练习解析函数的洛朗级数展开 3泰勒展开定理, e,sinz,cosz,ln(1+z),(1+z)“等函数的泰 勒展式,函数展开成幂级数(泰勒级数)的直 接展开法和间接展开法,收敛半径。 4双边幂级数概念和性质,洛朗展开定理,函 数展开成洛朗级数的间接展开法。 第五章留数 自学内容:预习孤立奇点的定义 5.1解析函数的孤立奇点 5.2留数的一般理论 课堂作业: 5.3留数在计算定积分和反常积分中的应用 讨论几类孤立奇点的区别 35
35 2.5 调和函数 知识点: 1.复变函数极限的概念,定理。 2.复变函数连续的概念,定理。 3.复变函数导数的概念,导数的运算法则,函 数可导的充要条件,高阶导数 4.解析函数的概念,初等函数的解析性,函数 解析的充要条件。 5.调和函数和共轭调和函数的概念,解析函数 与调和函数的关系。 数的区别 课外作业: 1.完成本章小结 2.练习计算复变函数的极限 3.练习判断复变函数的连续 4.练习计算复变函数的导数 5.连续判断解析函数的方法 第三章 积分 3.1 积分的概念、性质与计算 3.2 柯西基本定理及推广 3.3 柯西积分公式及推论 3.4 解析函数的导数 知识点: 1.复积分的概念及基本性质,曲线积分法,参 数方程法和积分估值公式。 2.柯西基本定理及推广复合闭路定理,原函数 存在定理及牛顿-莱布尼兹公式。 3.柯西积分公式及高阶导数公式,解析函数的 平均值定理、无穷可微性,沿闭曲线的复积分。 4.解析函数的各阶导数及其解析性。 自学内容:复习高等数学中函数积分概念 课堂作业: 讨论复变函数与实变函数的积分区别 课外作业: 1.完成本章小结 2.练习计算复变函数的积分 3.练习柯西定理的使用 第四章 级数 4.1 收敛序列与收敛级数 4.2 幂级数 4.3 泰勒级数 4.4 洛朗级数 知识点: 1.复数列极限、复级数收敛、发散概念,与高 等数学中相应内容的关系。 2.幂级数概念, Abel 定理,幂级数收敛半径 求法、幂级数的运算及性质。 3.泰勒展开定理, e ,sin z, cos z,ln(1 z),(1 z) z 等函数的泰 勒展式,函数展开成幂级数(泰勒级数)的直 接展开法和间接展开法,收敛半径。 4.双边幂级数概念和性质,洛朗展开定理,函 数展开成洛朗级数的间接展开法。 自学内容:复习高等数学中级数概念 课堂作业: 讨论复变函数与高等数学中级数的区别 课外作业: 1.完成本章小结 2.练习判断收敛序列 3.练习确定收敛级数的半径 4.练习解析函数的泰勒级数展开 5.练习解析函数的洛朗级数展开 第五章 留数 5.1 解析函数的孤立奇点 5.2 留数的一般理论 5.3 留数在计算定积分和反常积分中的应用 自学内容:预习孤立奇点的定义 课堂作业: 讨论几类孤立奇点的区别

知识点: 1孤立奇点的定义、分类及特征,零点与极点 课外作业: 的关系。 1完成本章小结 2.留数概念,留数的计算 2.练习使用留数计算定积分和反常积分 3利用留数定理计算闭路复积分,围道积分 法,用留数计算下面三种类型的定积分: R(eos0,sindo,∫R(xk,∫Rxe- 第二篇积分变换 自学内容:复习高等数学课程中傅里叶级数 第一章傅里叶变换 的概念 1.1 Fourier积分 课堂作业: 1.2 Fourier变换 讨论傅里叶级数和傅里叶积分的区别 l.36函数及其Fourier变换 课外作业: 知识点: 1完成本章小结 L.周期函数的Fourier级数形式,Fourier积分 2.练习工程技术中常用的一些函数的傅里 定理,Fourier积分公式的三角形式,Fourier 叶变换 正弦、余弦积分公式。 3练习借助单位脉冲函数的筛选性质求函 2.Fourier变换的概念,理解其性质,常用函数 数的傅里叶变换 的Fourier变换的求法。 3.6函数的概念及其性质,6函数的傅里叶变 换。 第二章Laplace拉普拉斯变换 自学内容:拉普拉斯积分的定义 2.1 Laplace变换的概念 课堂作业: 2.2 Laplace逆变换 讨论拉普拉斯变换和傅里叶变换的区别 2.3 Laplace变换的性质 课外作业: 2.4 Laplace变换的应用 1完成本章小结 知识点: 2.练习计算常用函数的拉普拉斯变换和逆 l.Laplace变换的概念及与Fourier变换的联系 变换 与区别 3.练习借助拉普拉斯变换的方法求解线性 2.Laplace变换及其逆变换的概念,反演积分公 微分方程 式,用留数求Laplace逆变换的方法。 3.Laplace变换存在定理,基本函数的Laplace 变换、Laplace变换的性质及卷积定理,运用 Laplace变换的性质求函数的Laplace变换及逆 变换。 4.应用Laplace变换解常系数线性微分方程的 方法,某些积分方程的Laplace变换解法。 五、建议学时分配表 序号 学时分配 对应教学目标 36
36 知识点: 1.孤立奇点的定义、分类及特征,零点与极点 的关系。 2.留数概念,留数的计算 3.利用留数定理计算闭路复积分,围道积分 法,用留数计算下面三种类型的定积分: R d R x dx R x e dx iax (cos ,sin ) , ( ) , ( ) 2 0 课外作业: 1.完成本章小结 2.练习使用留数计算定积分和反常积分 第二篇 积分变换 第一章 傅里叶变换 1.1 Fourier 积分 1.2 Fourier 变换 1.3 函数及其 Fourier 变换 知识点: 1.周期函数的 Fourier 级数形式,Fourier 积分 定理,Fourier 积分公式的三角形式,Fourier 正弦、余弦积分公式。 2.Fourier 变换的概念,理解其性质,常用函数 的 Fourier 变换的求法。 3. 函数的概念及其性质, 函数的傅里叶变 换。 自学内容:复习高等数学课程中傅里叶级数 的概念 课堂作业: 讨论傅里叶级数和傅里叶积分的区别 课外作业: 1.完成本章小结 2.练习工程技术中常用的一些函数的傅里 叶变换 3.练习借助单位脉冲函数的筛选性质求函 数的傅里叶变换 第二章 Laplace 拉普拉斯变换 2.1 Laplace 变换的概念 2.2 Laplace 逆变换 2.3 Laplace 变换的性质 2.4 Laplace 变换的应用 知识点: 1.Laplace 变换的概念及与 Fourier 变换的联系 与区别 2.Laplace 变换及其逆变换的概念,反演积分公 式,用留数求 Laplace 逆变换的方法。 3.Laplace 变换存在定理,基本函数的 Laplace 变换、Laplace 变换的性质及卷积定理,运用 Laplace变换的性质求函数的Laplace变换及逆 变换。 4.应用 Laplace 变换解常系数线性微分方程的 方法,某些积分方程的 Laplace 变换解法。 自学内容:拉普拉斯积分的定义 课堂作业: 讨论拉普拉斯变换和傅里叶变换的区别 课外作业: 1.完成本章小结 2.练习计算常用函数的拉普拉斯变换和逆 变换 3.练习借助拉普拉斯变换的方法求解线性 微分方程 五、建议学时分配表 序号 学 时 分 配 对应教学目标

课程内容 讲授 实验 习题 小计 第一章复数与复变函 目标1 第 复 第二章导数 6 6 目标1、2、3 篇 变 函 第三章积分 6 6 目标1、5 数 第四章级数 6 6 目标1、4 第五章留数 6 6 目标1、4 6 第 第一章傅里叶变换 6 目标1、6 篇 分变换 第二章拉普拉斯变换 6 6 目标1、6 合计 40 40 六、教学方法(本课程的主要教学方法) 复变函数与积分变换的理论课程学习,主要的教学方法为课堂讲授,具体内容包括: 1、授课方式多采用启发式教学,这样不仅可以激发学生学习兴趣,还可以培养学生思考、 分析、解决问题的能力。由于内容、概念、理论较多,要求学生课前要进行预习。 2、采用多媒体与板书相结合的教学方式,提高课堂教学的信息含量,增强教学的直观性。3、 适当采用课内讨论的教学方式,增强学习氛围,培养学生思考问题、分析问题、并将所学知 识运用到问题中的应用能力。 4、布置课后作业及安排课外答疑。 七、课程考核内容及方法 1.考核方式考试 2.考核形式包括平时考核、期中考核、期末考核等综合评定 3成绩评定采用百分制制,按以下3项考核指标进行成绩综合评定,其构成比例如下: 平时考核成绩:占课程总成绩的30%;(其中考勤占10%,作业占10%,课堂表现 占10%) 期中考核成绩:占课程总成绩的10%; 期末考核成绩:占课程总成绩的60%: 八、推荐教材和教学参考书 教材:《复变函数与积分变换((第3版)》,苏变萍,陈东立编著,高等教育出版社,2018年。 参考书:《复变函数与积分变换学习辅导与习题全解(第3版)》,王一平,苏变萍编著,高 等教育出版社,2018年。 37
37 课程内容 讲 授 实验 习题 课 小计 1 复 变 函 数 第 一 篇 第一章 复数与复变函 数 4 4 目标 1 2 第二章 导数 6 6 目标 1、2、3 3 第三章 积分 6 6 目标 1、5 4 第四章 级数 6 6 目标 1、4 5 第五章 留数 6 6 目标 1、4 6 积 分 变 换 第 二 篇 第一章 傅里叶变换 6 6 目标 1、6 7 第二章 拉普拉斯变换 6 6 目标 1、6 合 计 40 40 六、教学方法(本课程的主要教学方法) 复变函数与积分变换的理论课程学习,主要的教学方法为课堂讲授,具体内容包括: 1、授课方式多采用启发式教学,这样不仅可以激发学生学习兴趣,还可以培养学生思考、 分析、解决问题的能力。由于内容、概念、理论较多,要求学生课前要进行预习。 2、采用多媒体与板书相结合的教学方式,提高课堂教学的信息含量,增强教学的直观性。3、 适当采用课内讨论的教学方式,增强学习氛围,培养学生思考问题、分析问题、并将所学知 识运用到问题中的应用能力。 4、布置课后作业及安排课外答疑。 七、课程考核内容及方法 1.考核方式 考试 2.考核形式 包括平时考核、期中考核、期末考核等综合评定 3.成绩评定 采用百分制制,按以下 3 项考核指标进行成绩综合评定,其构成比例如下: 平时考核成绩:占课程总成绩的 30%;(其中考勤占 10%,作业占 10%,课堂表现 占 10%) 期中考核成绩:占课程总成绩的 10%; 期末考核成绩:占课程总成绩的 60%; 八、推荐教材和教学参考书 教 材:《复变函数与积分变换(第 3 版)》,苏变萍,陈东立编著,高等教育出版社,2018 年。 参考书:《复变函数与积分变换学习辅导与习题全解(第 3 版)》,王一平,苏变萍编著,高 等教育出版社,2018 年