
>定理1即四=A分)=m()=A x->x0
➢定理1 f x A f x f x A x x x x x x = = = → → + → − lim ( ) lim ( ) lim ( ) 0 0 0

函数的变化趋势 有趋势 无趋势 趋势为 趋势为 无界 有界 常数4 无穷大 振荡 A0 A=0 n->oo 有极限、 无穷小∞ +。0 x→+o0 自变量的变化过程 x>-0 X-> >x0 →xd 今x0
函数的变化趋势 自变量的变化过程 有趋势 x →+ x → − x → → − x x 0 → + x x 00 x → x n → 无趋势 趋势为 常数A 趋势为 无穷大 A≠0 A=0 ∞ + ∞ - ∞ 无界 有界 振荡 有极限 无穷小

>定理1imf(x)=A→1imf(x)=imf(x)=A xx0 x-→x0 x→x0 >定理2limf(x)=A÷limf(x)=1imf(x)=A
➢定理1 f x A f x f x A x x x x x x = = = → → + → − lim ( ) lim ( ) lim ( ) 0 0 0 ➢定理2 f x A f x f x A x x x = = = → →− →+ lim ( ) lim ( ) lim ( )
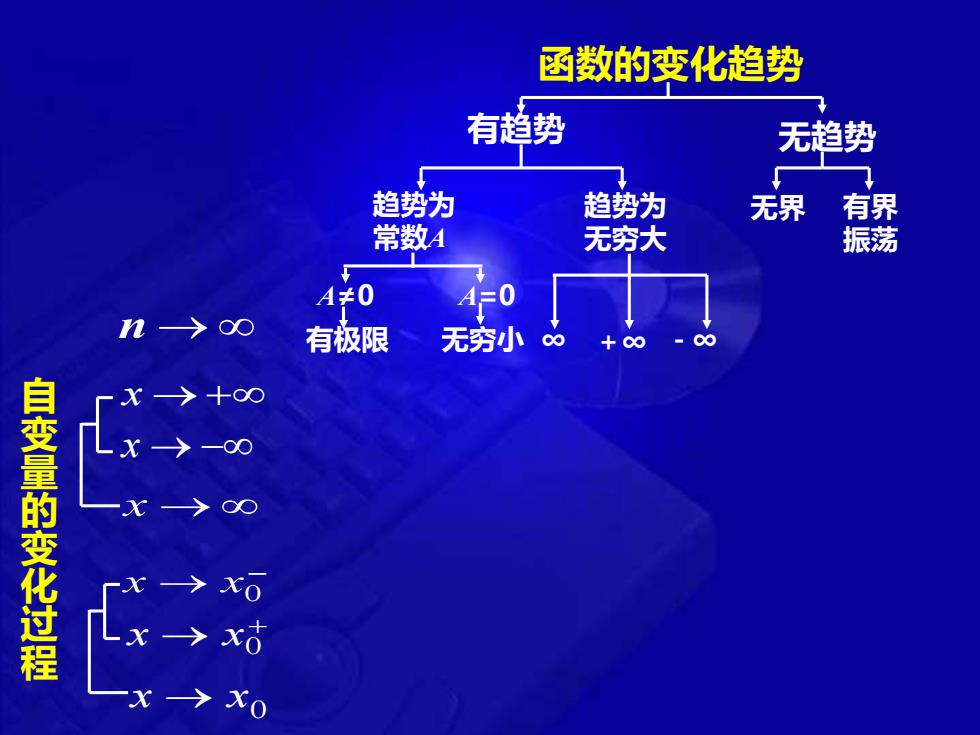
函数的变化趋势 有趋势 无趋势 趋势为 趋势为 无界 有界 常数4 无穷大 振荡 A0 A=0 n->oo 有极限 无穷小∞ +。0 自变量的变化过程 Lx>-0 >x0 >x x0
函数的变化趋势 自变量的变化过程 有趋势 x →+ x → − x → → − x x 0 → + x x 00 x → x n → 无趋势 趋势为 常数A 趋势为 无穷大 A≠0 A=0 ∞ + ∞ - ∞ 无界 有界 振荡 有极限 无穷小

>定理1 lim f(x)=A lim f(x)=lim f(x)=A xx0 x-→x0 x→x0 >定理2limf(x)=A兮imf(x)=imf(c)=A >定理3 limx=A limx =4 (( 1-→c0 k=→00
➢定理1 f x A f x f x A x x x x x x = = = → → + → − lim ( ) lim ( ) lim ( ) 0 0 0 ➢定理2 f x A f x f x A x x x = = = → →− →+ lim ( ) lim ( ) lim ( ) ➢定理3 lim lim ({ } { }) k k n n n n n k x A x A x x → → = =