+例:抛硬币出现的正面的频率 表1 试验 n=5 n=50 n=500 序号 n f(0 nt f(00 n f(H) 1 2 0.4 22 0.44 251 0.502 3 0.6 25 0.50 249 0.498 234 1 0.2 21 0.42 256 0.512 5 1.0 25 0.50 253 0.506 1 0.2 24 0.48 251 0.502 56789 2 0.4 21 0.42 246 0.492 4 0.8 18 0.36 244 0.488 2 0.4 24 0.48 258 0.516 3 0.6 27 0.54 262 0.524 10 3 0.6 31 0.62 247 0.494
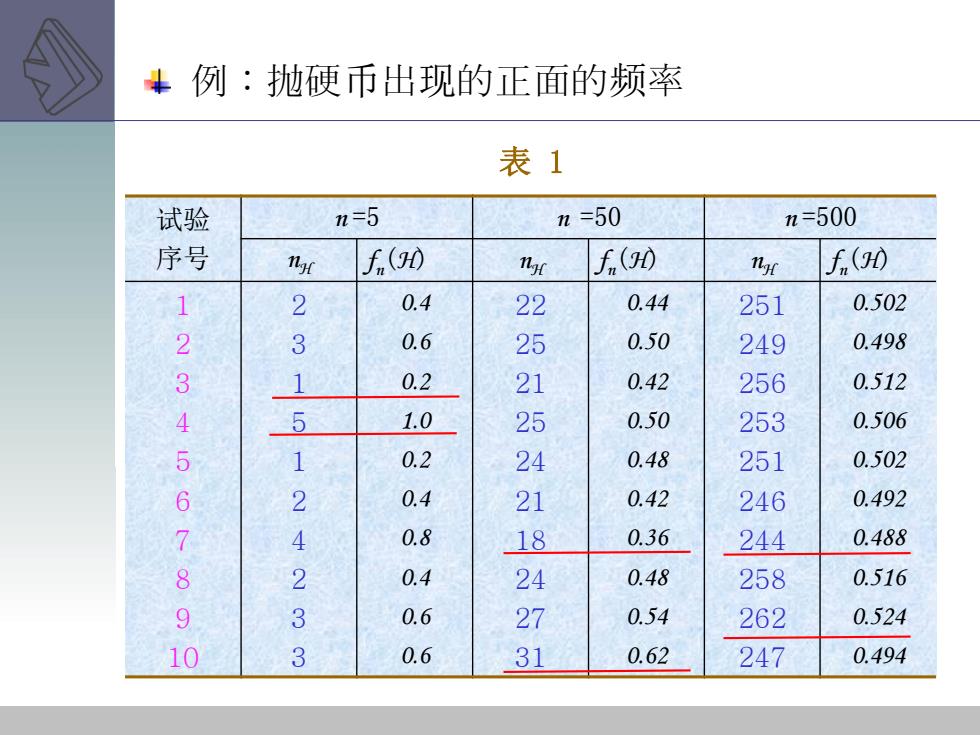
试验 序号 n =5 n =50 n =500 nH f n(H) nH f n(H) nH f n(H) 1 2 3 4 5 6 7 8 9 10 2 3 1 5 1 2 4 2 3 3 0.4 0.6 0.2 1.0 0.2 0.4 0.8 0.4 0.6 0.6 22 25 21 25 24 21 18 24 27 31 0.44 0.50 0.42 0.50 0.48 0.42 0.36 0.48 0.54 0.62 251 249 256 253 251 246 244 258 262 247 0.502 0.498 0.512 0.506 0.502 0.492 0.488 0.516 0.524 0.494 表 1 例:抛硬币出现的正面的频率
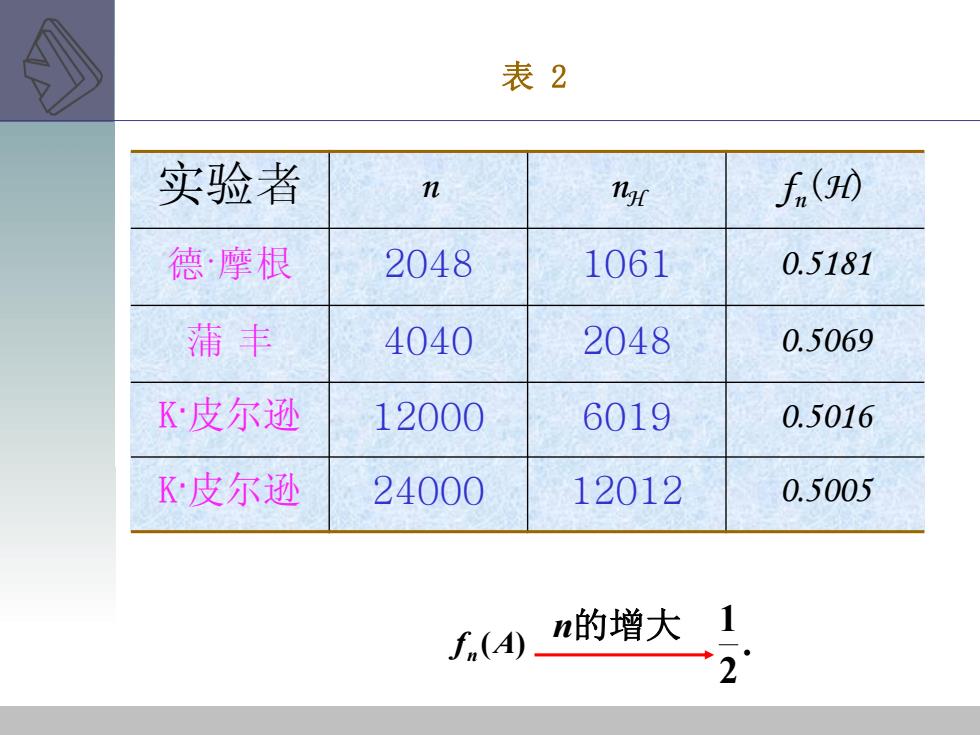
表2 实验者 n nyt f(0 德摩根 2048 1061 0.5181 蒲丰 4040 2048 0.5069 K皮尔逊 12000 6019 0.5016 K皮尔逊 24000 12012 0.5005 f(A) n的增大1 *21
实验者 n nH f n(H) 德·摩根 2048 1061 0.5181 蒲 丰 4040 2048 0.5069 K·皮尔逊 12000 6019 0.5016 K·皮尔逊 24000 12012 0.5005 表 2 . 2 n的增大 1 f (A) n

*频率的性质: 1° 0≤fn(A)≤1 2°fn(S)=1 若4,4,,4两两互不相容,则心4)-空(4) 3° 且f,()随的增大渐趋稳定,记稳定值为p
** 频率的性质: 且 f A n ( ) 随n的增大渐趋稳定,记稳定值为p. 1 2 1 1 1 0 ( ) 1 2 ( ) 1 3 , ( ) ( ) n n k k k n i n i i i f A f S A A A f A f A 。 。 。 若 ,…, 两两互不相容,则

二、概率的公理化定义 在学习几何和代数时,我们已经知道 公理是数学体系的基础.数学上所说的 6 公理”,就是一些不加证明而公认的前提 ,然后以此为基础,推演出所讨论对象的 进一步的内容
在学习几何和代数时,我们已经知道 公理是数学体系的基础. 数学上所说的“ 公理”,就是一些不加证明而公认的前提 ,然后以此为基础,推演出所讨论对象的 进一步的内容. 二、概率的公理化定义

1933年,前苏联数学家柯 尔莫哥洛夫给出了概率的公理 化定义。 即通过规定概率应具备的 柯尔莫哥洛夫,A.H 基本性质来定义概率 柯尔莫哥洛夫提出的公理为数很少且 极为简单,但在此基础上建立起了概率论 的宏伟大厦. 下面介绍用公理给出的概率定义
即通过规定概率应具备的 基本性质来定义概率. 下面介绍用公理给出的概率定义. 1933年,前苏联数学家柯 尔莫哥洛夫给出了概率的公理 化定义. 柯尔莫哥洛夫提出的公理为数很少且 极为简单, 但在此基础上建立起了概率论 的宏伟大厦